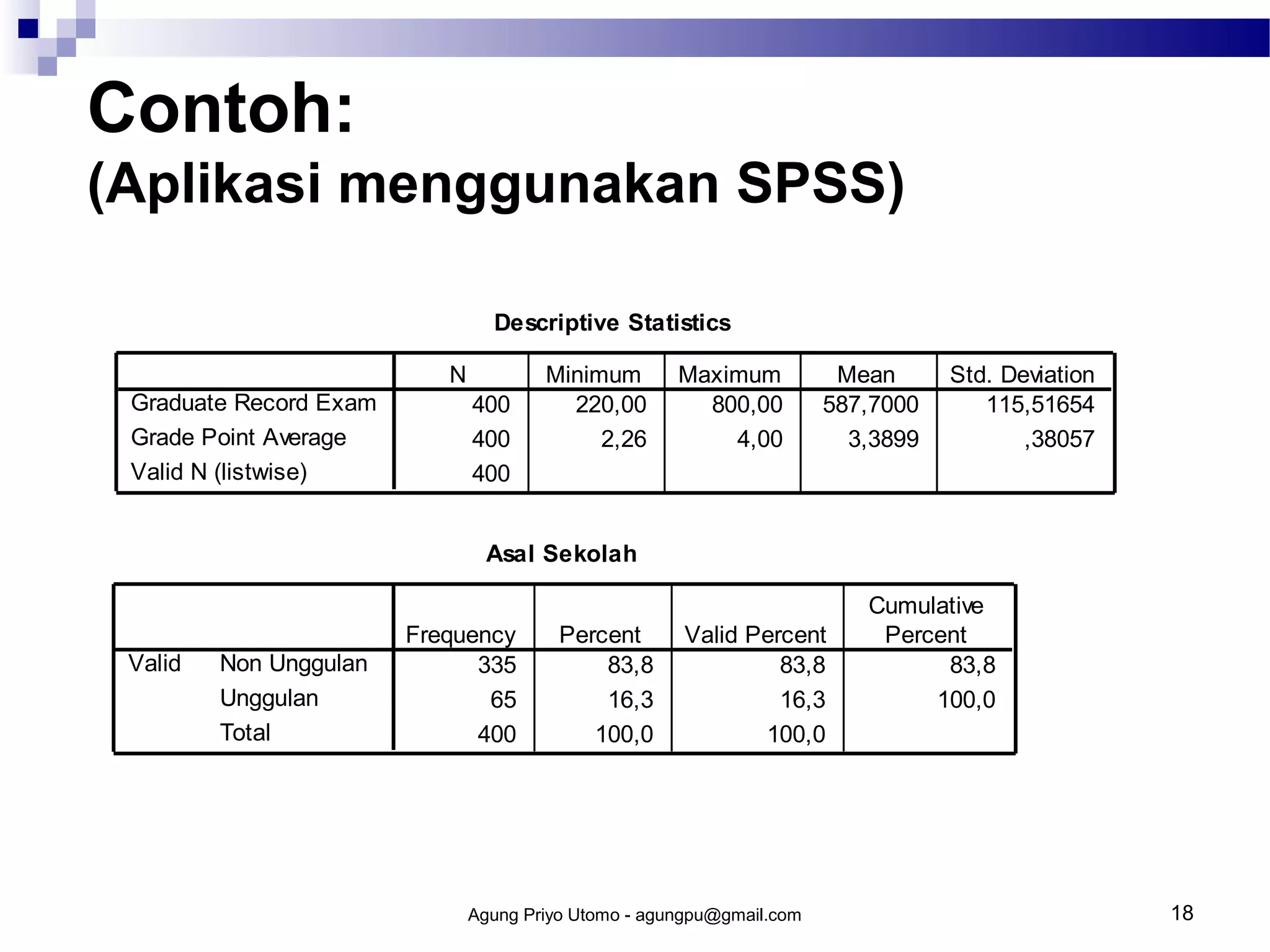
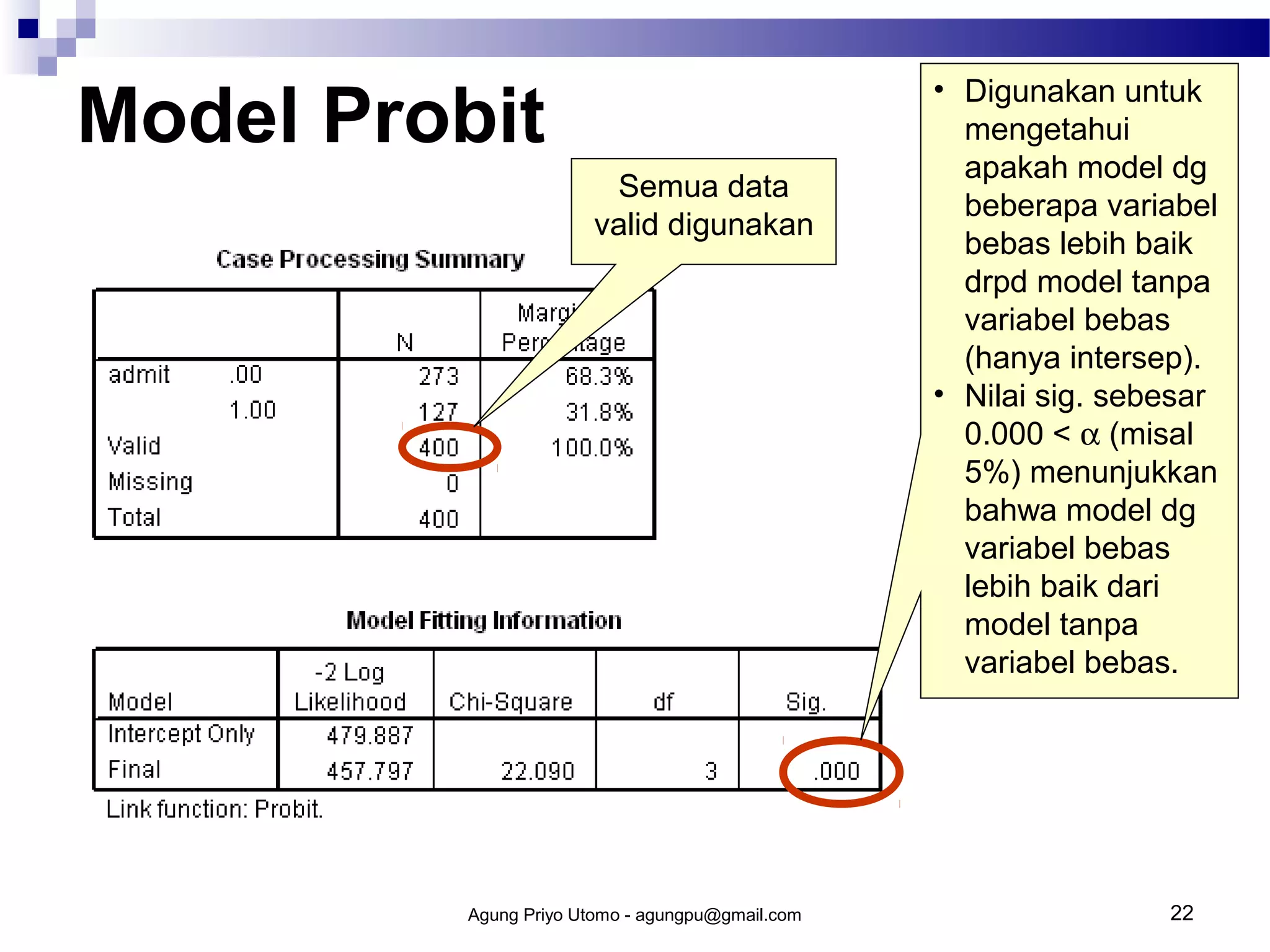
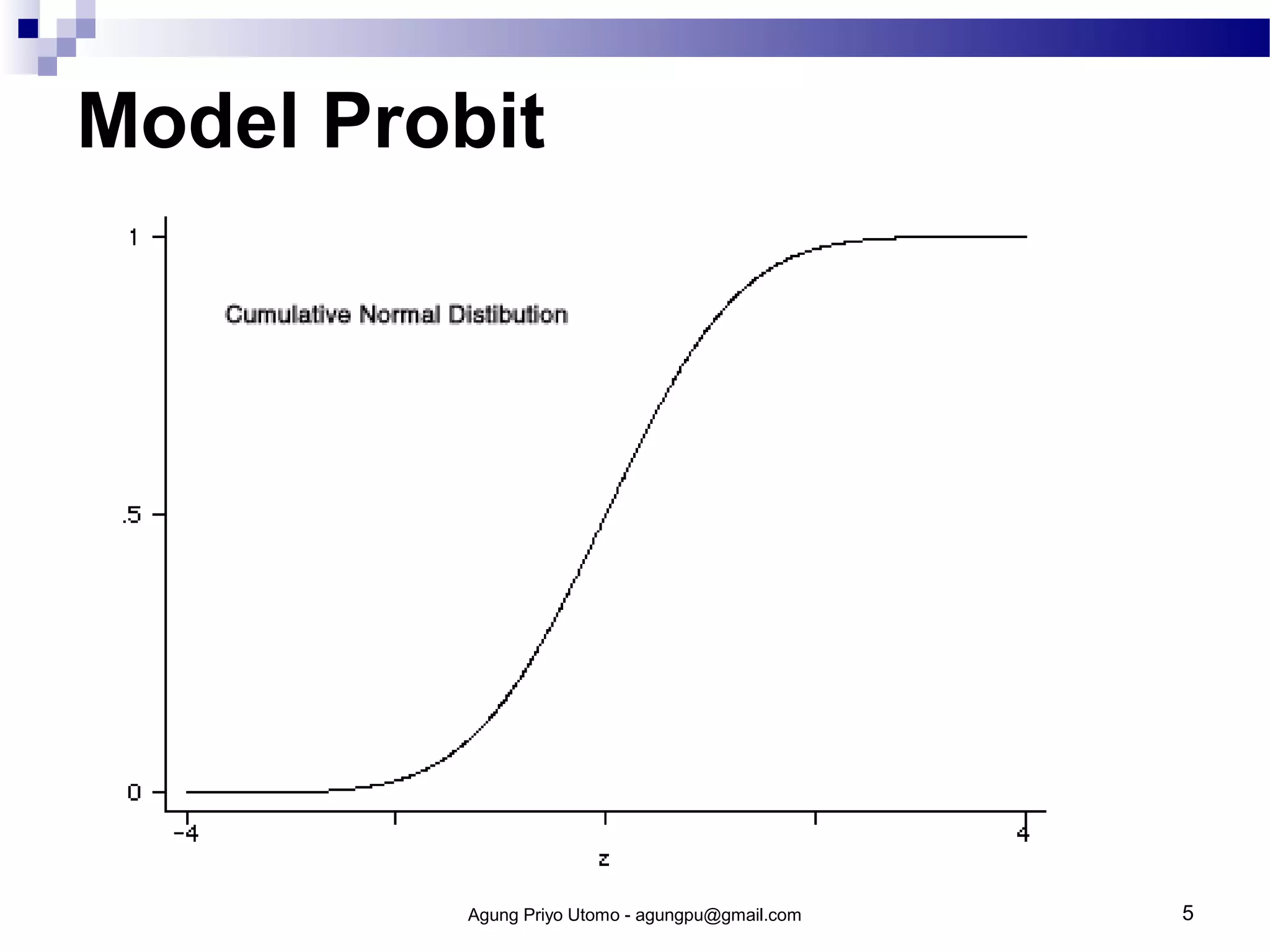
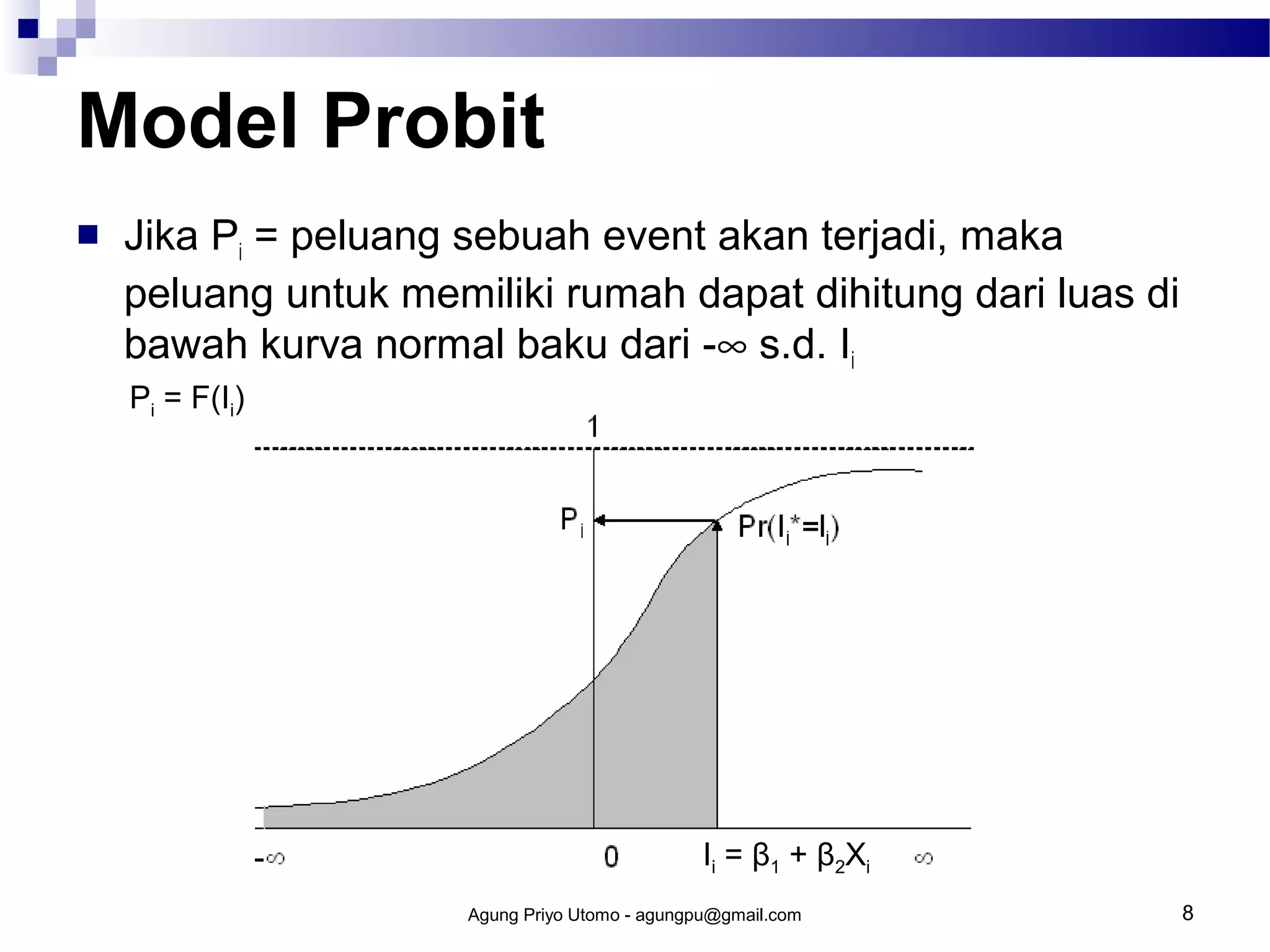
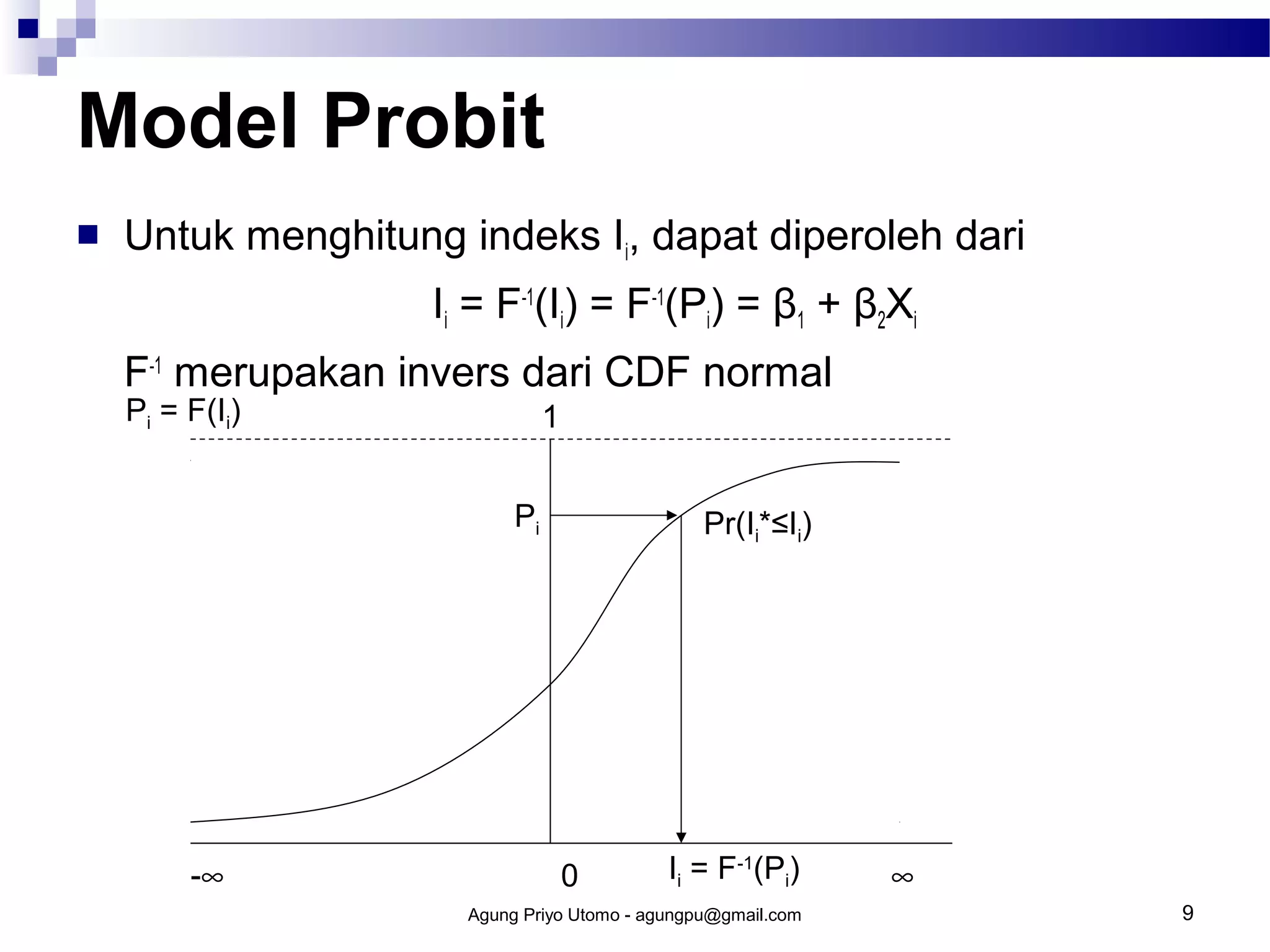
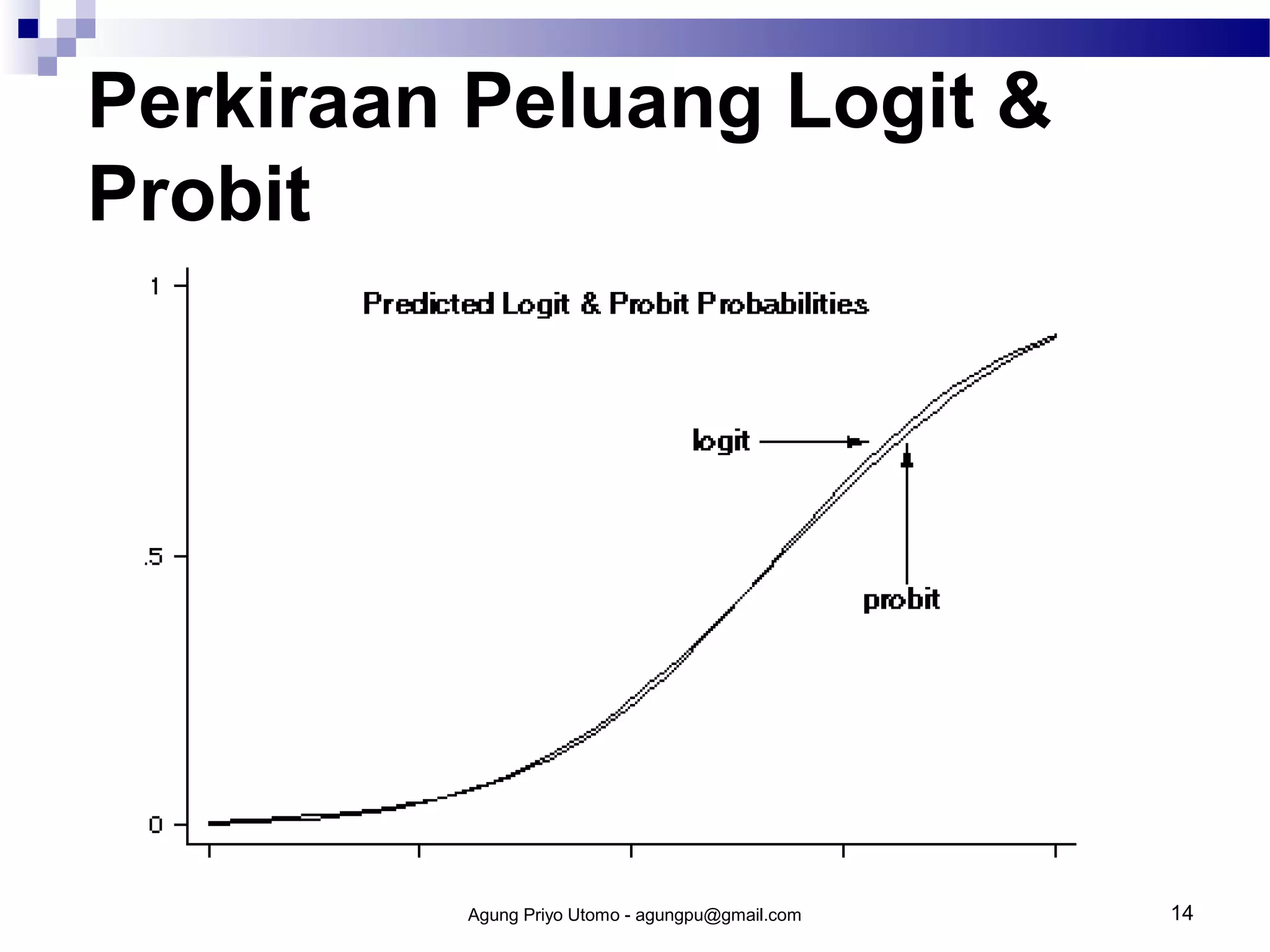
Ringkasan dokumen tersebut dalam 3 kalimat adalah: Model probit digunakan untuk memprediksi kemungkinan terjadinya suatu peristiwa berdasarkan faktor-faktor yang mempengaruhinya. Model ini menggunakan fungsi distribusi normal kumulatif untuk memperoleh indeks peluang. Cara kerja model probit meliputi estimasi peluang, perolehan indeks peluang, dan regresi untuk memperoleh parameter model.

1. MODEL PROBIT
BAHAN KULIAH EKONOMETRIKA
PROGRAM STUDI KAJIAN TIMUR TENGAH DAN ISLAM
UNIVERSITAS INDONESIA
Agung Priyo Utomo - agungpu@gmail.com
1

2. Model Probit

Contoh 1:
Penelitian untuk mengetahui faktor-faktor yang
mempengaruhi apakah seorang kandidat akan
memenangkan pemilu atau tidak. Dalam kasus ini maka
hasilnya adalah menang atau kalah. Beberapa faktor yg
diduga berpengaruh adalah besarnyauang yang
dikeluarkan dalam kampanye, lamanya waktu
berkampanye negatif dan apakah kandidat memiliki
jabatan atau tidak.

Contoh 2:
Penelitian untuk mengetahui apakah latihan OR, usia, dan
jenis kelamin berpengaruh terhadap seseorang akan
terkena serangan jantung atau tidak.
Agung Priyo Utomo - agungpu@gmail.com
2

3. Model Probit

Contoh 3:
Beberapa siswa SMU berkeinginan untuk melanjutkan
kuliah. Dalam berkas lamarannya, mereka memasukkan
skor GRE dan nilai GPA. Beberapa siswa berasal dari
sekolah unggulan dan ada juga yang dari sekolah non
unggulan. Beberapa bulan setelah siswa mengirimkan
aplikasi, siswa tersebut menerima 2 macam amplop (tebal
atau tipis) yang menandakan mereka diterima atau ditolak
di PT yang bersangkutan.
Agung Priyo Utomo - agungpu@gmail.com
3

4. Model Probit





Pertama kali ditemukan oleh Chester Bliss (1930)
Probit = Probability Unit
Model logit menggunakan fungsi logistik kumulatif
(cumulative logistic function)
Model probit menggunakan fungsi normal kumulatif
(normal CDF) → disebut juga dengan model normit
Secara prinsip utk memperoleh model probit dpt dilakukan
dg mengganti fungsi logistik kumulatif pd persamaan
1
Pi =
1 + e − Zi
dengan fungsi normal kumulatif
Agung Priyo Utomo - agungpu@gmail.com
4

5. Model Probit
Agung Priyo Utomo - agungpu@gmail.com
5

6. Model Probit



Contoh:
Keputusan untuk membeli/memiliki rumah dilihat dari
pendapatan keluarga.
Ada suatu nilai, semacam indeks kegunaan yg tdk dpt
diamati (unobservable utility index), misal Ii, sedemikian
sehingga makin besar nilai Ii, maka makin besar pula
peluang sebuah keluarga untuk membeli rumah.
Indeks Ii dapat dinyatakan sbb:
Ii = β1 + β2Xi
Xi = pendapatan keluarga ke-i
Agung Priyo Utomo - agungpu@gmail.com
6

7. Model Probit

Bgmn hubungan Ii dg keputusan utk membeli rumah?




Pada model logistik, Y = 1 jika keluarga memiliki rumah dan Y = 0
jika keluarga tidak memiliki rumah
Pada model probit, dapat diasumsikan untuk setiap keluarga ada
batasan indeks, misal Ii* sedemikian shg jika Ii > Ii*, maka keluarga
tersebut akan membeli rumah
Jika diasumsikan Ii* berdistribusi normal dengan rata-rata
dan varian sama, maka Ii* maupun Ii dapat diestimasi
Dibawah asumsi kenormalan, maka
Pi = P( Y = 1)
= P(Ii*
T
≤ Ii ) = F(Ii ) =
1 i − t2 2
∫ e dt =
2π − ∞
1
2π
β1 + β2 Xi
∫
e
−t
2
2
dt
−∞
dimana t ~ N(0,1)
Agung Priyo Utomo - agungpu@gmail.com
7

8. Model Probit

Jika Pi = peluang sebuah event akan terjadi, maka
peluang untuk memiliki rumah dapat dihitung dari luas di
bawah kurva normal baku dari -∞ s.d. Ii
Pi = F(Ii)
Ii = β1 + β2Xi
Agung Priyo Utomo - agungpu@gmail.com
8

9. Model Probit

Untuk menghitung indeks Ii, dapat diperoleh dari
Ii = F-1(Ii) = F-1(Pi) = β1 + β2Xi
F-1 merupakan invers dari CDF normal
Pi = F(Ii)
1
Pi
-∞
Pr(Ii*≤Ii)
0
Ii = F-1(Pi)
Agung Priyo Utomo - agungpu@gmail.com
∞
9

10. Model Probit


Bagaimana memperoleh indeks Ii, jika yg diketahui hanya
Xi (pendapatan) dan Y = 1 atau Y = 0 (tergantung apakah
keluarga tersebut memiliki rumah atau tidak)?
Misal datanya sbb: (X = dalam ribuan $)
X
Ni
ni
6
40
8
8
50
12
10
60
18
13
80
28
15
100
45
20
70
36
25
65
39
30
50
33
35
40
30
40
25
20
Agung Priyo Utomo - agungpu@gmail.com
10

11. Model Probit

Untuk mengestimasi indeks Ii dpt dilakukan melalui nilai
Peluang (frekuensi relatif), selanjutnya bandingkan
dengan CDF normal
X
Ni
ni
Est. Pi
Ii
6
40
8
0,20
-0.84
8
50
12
0,24
-0.70
10
60
18
0,30
-0.52
13
80
28
0,35
-0.38
15
100
45
0,45
-0.12
20
70
36
0,51
0.03
25
65
39
0,60
0.25
30
50
33
0,66
0.40
35
40
30
0,75
0.67
40
25
20
0,80
0.84
Agung Priyo Utomo - agungpu@gmail.com
11

12. Model Probit

Dari data tersebut, model probit dapat diperoleh sbb:





Berdasarkan est. Pi (frekuensi relatif), maka dapat diperoleh Ii dari
CDF normal (ada di tabel sebelumnya)
Setelah Ii diperoleh, maka dapat dicari β1 dan β2 dg mudah
Pada analisis probit, Ii disebut normal equivalent deviate
(n.e.d) atau disebut juga normit
Karena Ii atau n.e.d akan bernilai negatif (-) pada saat Pi <
0.5, maka dalam prakteknya ditabahkan dengan nilai 5
dan hasilnya disebut probit
probit = n.e.d + 5 = Ii + 5
β1 dan β2 dapat diestimasi berdasarkan model:
Ii = β1 + β2Xi + ui
; dimana ui = unsur gangguan
Agung Priyo Utomo - agungpu@gmail.com
12

13. Model Probit

Tahapan dalam model probit:
1. Dari data yang sudah dikelompokkan, estimasi Pi
(frekuensi relatif)
2. Berdasarkan estimasi dari Pi, cari n.e.d (Ii) dari CDF
normal
3. Gunakan estimasi Ii (Ii*), sebagai variabel terikat dalam
regresi
Ii* = β1 + β2Xi + ui
4. Jika diperlukan, tambahkan 5 pada nilai n.e.d (Ii) untuk
mengubah menjadi probit dan gunakan sebagai
variabel terikat pada
Ii* = β1 + β2Xi + ui
Agung Priyo Utomo - agungpu@gmail.com
13

14. Perkiraan Peluang Logit &
Probit
Agung Priyo Utomo - agungpu@gmail.com
14

15. Logit atau Probit?




Logistic didasarkan pada kondisi dimana variabel tak
bebasnya bersifat kualitatif (menggunakan fungsi logit)
Probit didasarkan pada kondisi dimana variabel tak
bebasnya bersifat kuantitatif (menggunakan distribusi
kumulatif normal)
Dalam prakteknya kedua model seringkali memberikan
hasil yang sama/mirip.
Probit lebih mudah diinterpretasikan.
Agung Priyo Utomo - agungpu@gmail.com
15

16. Contoh:
(Aplikasi menggunakan SPSS)


Beberapa siswa SMU berkeinginan untuk melanjutkan
kuliah. Dalam berkas lamarannya, mereka memasukkan
skor GRE dan nilai GPA. Beberapa siswa berasal dari
sekolah unggulan dan ada juga yang dari sekolah non
unggulan. Beberapa bulan setelah siswa mengirimkan
aplikasi, siswa tersebut menerima 2 macam amplop
(tebal atau tipis) yang menandakan mereka diterima atau
ditolak di PT yang bersangkutan.
Data ada di file probit.sav
Agung Priyo Utomo - agungpu@gmail.com
16

17. Contoh:
(Aplikasi menggunakan SPSS)


Variabel tak bebas/terikat = admit
 1 = diterima (admitted)
 0 = tidak diterima (not admitted)
Variabel bebas =
 gre (graduate record exam score),
 gpa (grade point average),
 topnotch (asal sekolah) :
- 1 jika berasal dari sekolah ungulan
- 0 jika berasal dari sekolah non unggulan
Agung Priyo Utomo - agungpu@gmail.com
17

18. Contoh:
(Aplikasi menggunakan SPSS)
Descriptive Statistics
N
Graduate Record Exam
Grade Point Average
Valid N (listwise)
400
400
400
Minimum
220,00
2,26
Maximum
800,00
4,00
Mean
587,7000
3,3899
Std. Deviation
115,51654
,38057
Asal Sekolah
Valid
Non Unggulan
Unggulan
Total
Frequency
335
65
400
Percent
83,8
16,3
100,0
Valid Percent
83,8
16,3
100,0
Agung Priyo Utomo - agungpu@gmail.com
Cumulative
Percent
83,8
100,0
18

19. Beberapa Strategi



Regresi OLS
Analisis ini akan bermasalah, karena asumsi OLS akan
terlanggar jika digunakan pada kasus variabel terikatnya
berupa kategorik.
Uji t
Uji ini bisa digunakan jika kasusnya hanya terdiri dari
satu variabel bebas dan bersifat kuantitatif, misal hanya
melihat pengaruh dari GPA terhadap diterima atau
tidaknya seorang siswa di PT.
Regresi Logit
Model ini sangat mirip dengan model probit
Agung Priyo Utomo - agungpu@gmail.com
19

20. Penggunaan Model Probit

Sebelum menjalankan model probit, maka periksa dulu
apakah ada sel yang kosong/terlalu kecil frekuensinya
(pada tabulasi silang antara variabel bebas kategorik dan
variabel tak bebasnya). Jika terdapat sel yang kosong,
maka akan sulit menjalankan model probit.
Admission Status * Asal Sekolah Crosstabulation
Count
Admission
Status
Total
not admitted
admitted
Asal Sekolah
Non
Unggulan
Unggulan
238
35
97
30
335
65
Agung Priyo Utomo - agungpu@gmail.com
Tidak ada
sel yang kosong
Total
273
127
400
20

21. Model Probit

Sebelum menjalankan model probit, maka periksa dulu
apakah ada sel yang kosong/terlalu kecil frekuensinya
(pada tabulasi silang antara variabel bebas kategorik dan
variabel tak bebasnya). Jika terdapat sel yang kosong,
maka akan sulit menjalankan model probit.
Karena GPA dan GRE
kuantitatif/kontinu
Agung Priyo Utomo - agungpu@gmail.com
21

22. Model Probit
Semua data
valid digunakan
Agung Priyo Utomo - agungpu@gmail.com
• Digunakan untuk
mengetahui
apakah model dg
beberapa variabel
bebas lebih baik
drpd model tanpa
variabel bebas
(hanya intersep).
• Nilai sig. sebesar
0.000 < α (misal
5%) menunjukkan
bahwa model dg
variabel bebas
lebih baik dari
model tanpa
variabel bebas.
22