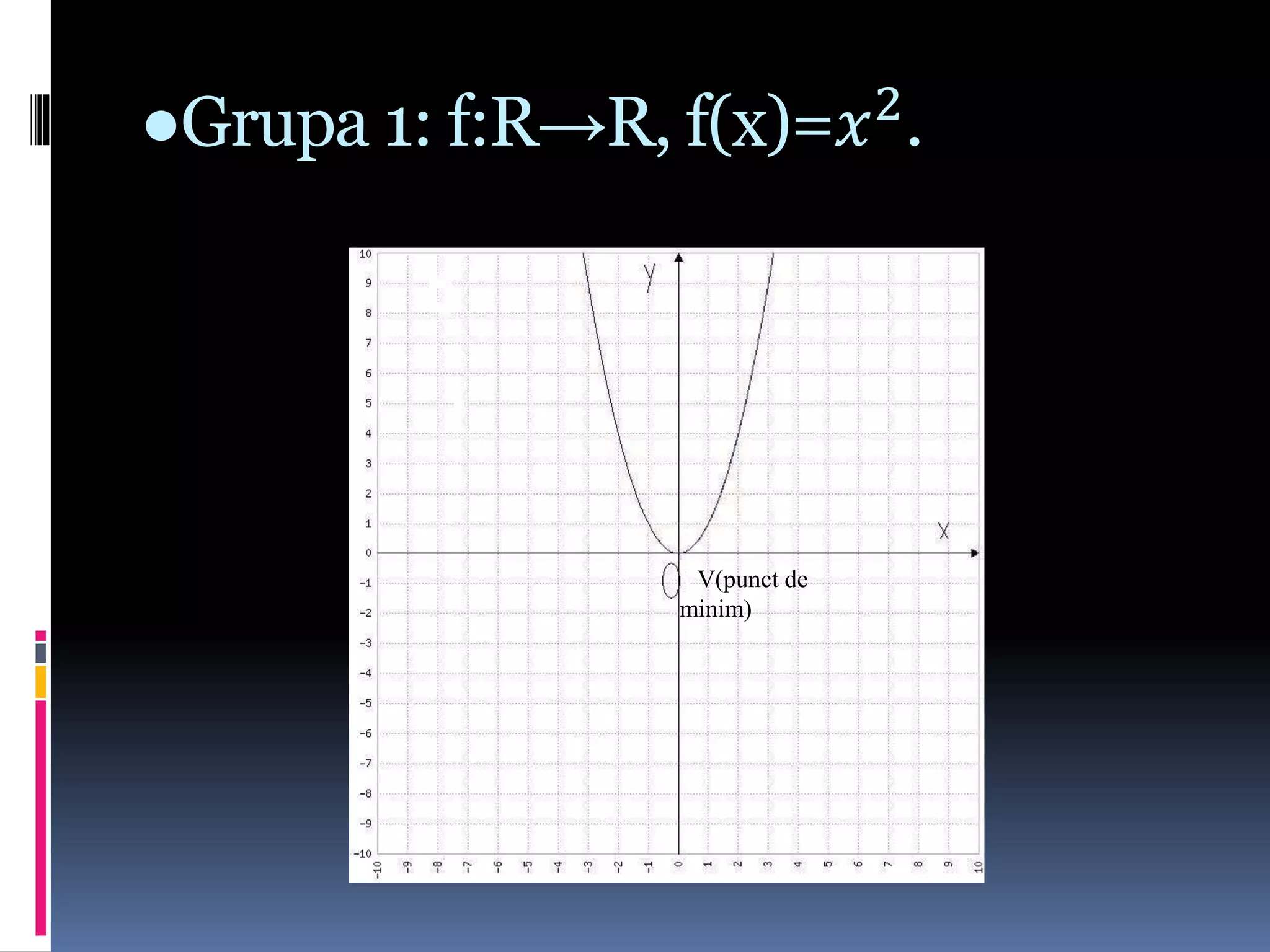
Funcția de gradul II are forma f(x)=ax²+bx+c, cu coeficienți a, b, c reali și a diferit de zero. Graficul acestei funcții este o parabolă, iar intersecția cu axele de coordonate se determină rezolvând ecuația ax²+bx+c=0. Extremul parabolei (punct de minim sau maxim) depinde de semnul lui a, iar axa de simetrie este dată de x=-b/2a.

1. REPREZENTAREA
GRAFICĂ A FUNCŢIEI
DE GRADUL II
PROF. ŢIGLEA OANA

2. Ne amintim!
 Definiţie: Funcţia f:R→R,
f(x)=ax2+bx+c, a,b,c €R şi a≠0 se
numeşte funcţia de gradul II.
 Ecuaţia ax2+bx+c=0 este ecuaţia
de gradul 2 ataşată acestei funcţii
 -a,b= coeficienţi
 c=termenul liber

3. Reprezentarea grafică a
funcţiei de gradul II
1. Intersecţia graficului cu
axele de coordonate
●Gf∩ 𝑶𝒙 => 𝒚 = 𝟎
ş𝒊 𝒔𝒆 𝒓𝒆𝒛𝒐𝒍𝒗ă 𝒆𝒄𝒖𝒂ţ𝒊𝒂 𝒇 𝒙 =0
ax2+bx+c=0, ∆=𝑏2
− 4𝑎𝑐
Gf ∩ 𝑶𝒙 = { A(x1,0) şi B(x2,0)}.
● Gf ∩ 𝑶𝒚 => 𝒙 = 𝟎 şi se calculează
f(0) => Gf ∩ 𝑶𝒚 = 𝑪(𝟎, 𝒇(𝟎)

4. 2.Puncte de extrem
 Dacă a>0 atunci punctul V( 𝑥 𝑉=
−𝑏
2𝑎
, 𝑦 𝑉 =
−∆
4𝑎
) este punct de minim şi 𝑦 𝑉este
valoarea minimă a funcţiei.
 Dacă a<0 atunci punctul V( 𝑥 𝑉=
−𝑏
2𝑎
, 𝑦 𝑉 =
−∆
4𝑎
) este punct de maxim şi 𝑦 𝑉este
valoarea maximă a funcţiei.

5. 3. Axa de simetrie a parabolei
Teoremă : Fie funcţia f:R→R,
f(x)=ax2+bx+c, a,b,c €R şi a≠0. Dreapta
verticală x=
−𝑏
2𝑎
este axă de simetrie pentru
graficul funcţiei f.

6. 4.Reprezentarea grafică
 Din punct de vedere geometric graficul
funcţiei de gradul II este o parabolă.

7. Graficul funcţiei de gradul
II
Dacă a>0
Dacă a<0

9. REPREZENTAŢI GRAFIC
FUNCŢIILE
 ●Grupa 1: f:R→R, f(x)=𝑥2
.
 ●Grupa 2: f:R→R, f(x)=2𝑥2
+ 4x+5
 ●Grupa 3: f:R→R, f(x)=−𝑥2
+ 2x-5

10. ●Grupa 1: f:R→R, f(x)=𝑥2
.
VV(punct de
minim)

11. ●Grupa 2: f:R→R, f(x)=2𝑥2
+ 4x+5
Punct de
minim

12. ●Grupa 3: f:R→R, f(x)=−𝑥2
+ 2x-5
V(punct de
maxim)
Punct
de
maxim