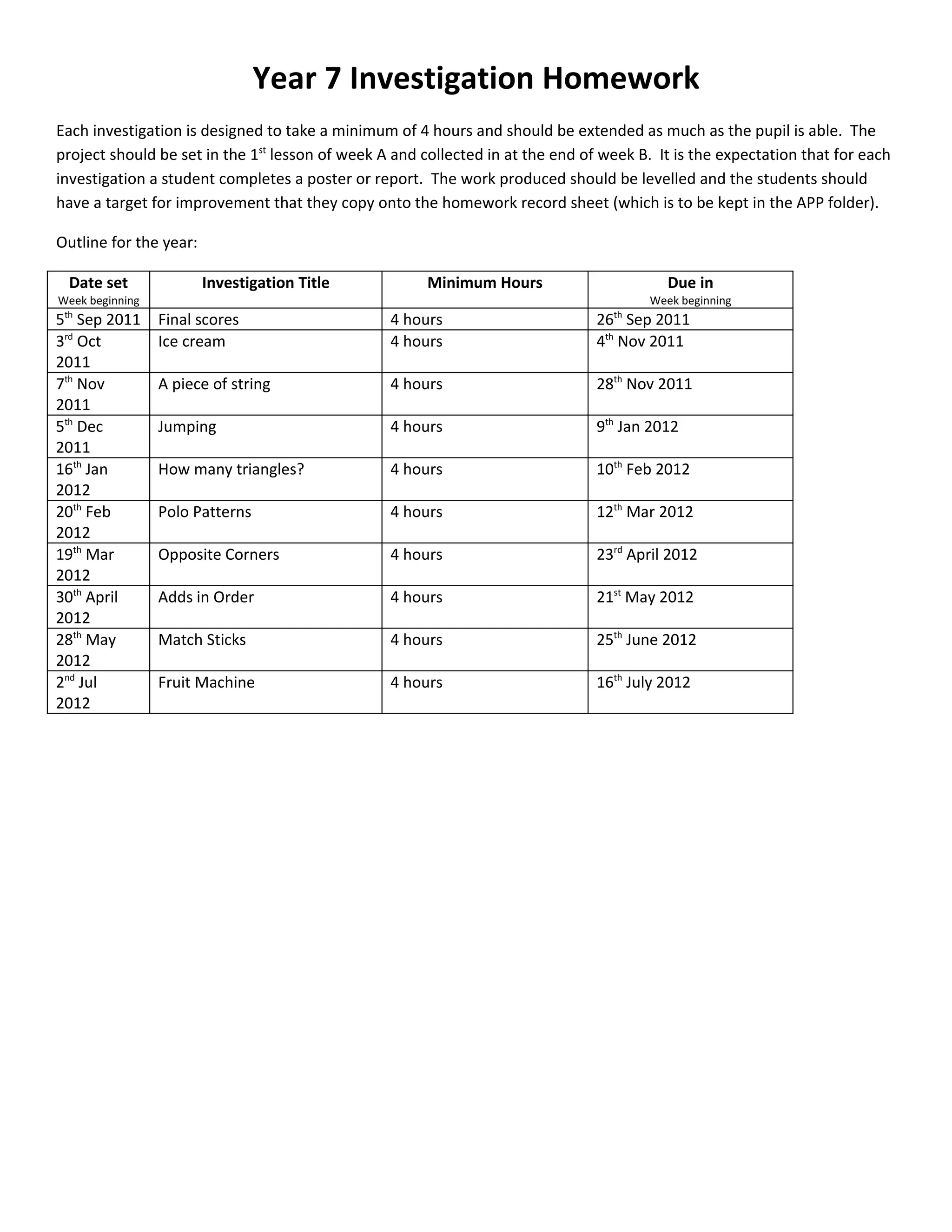
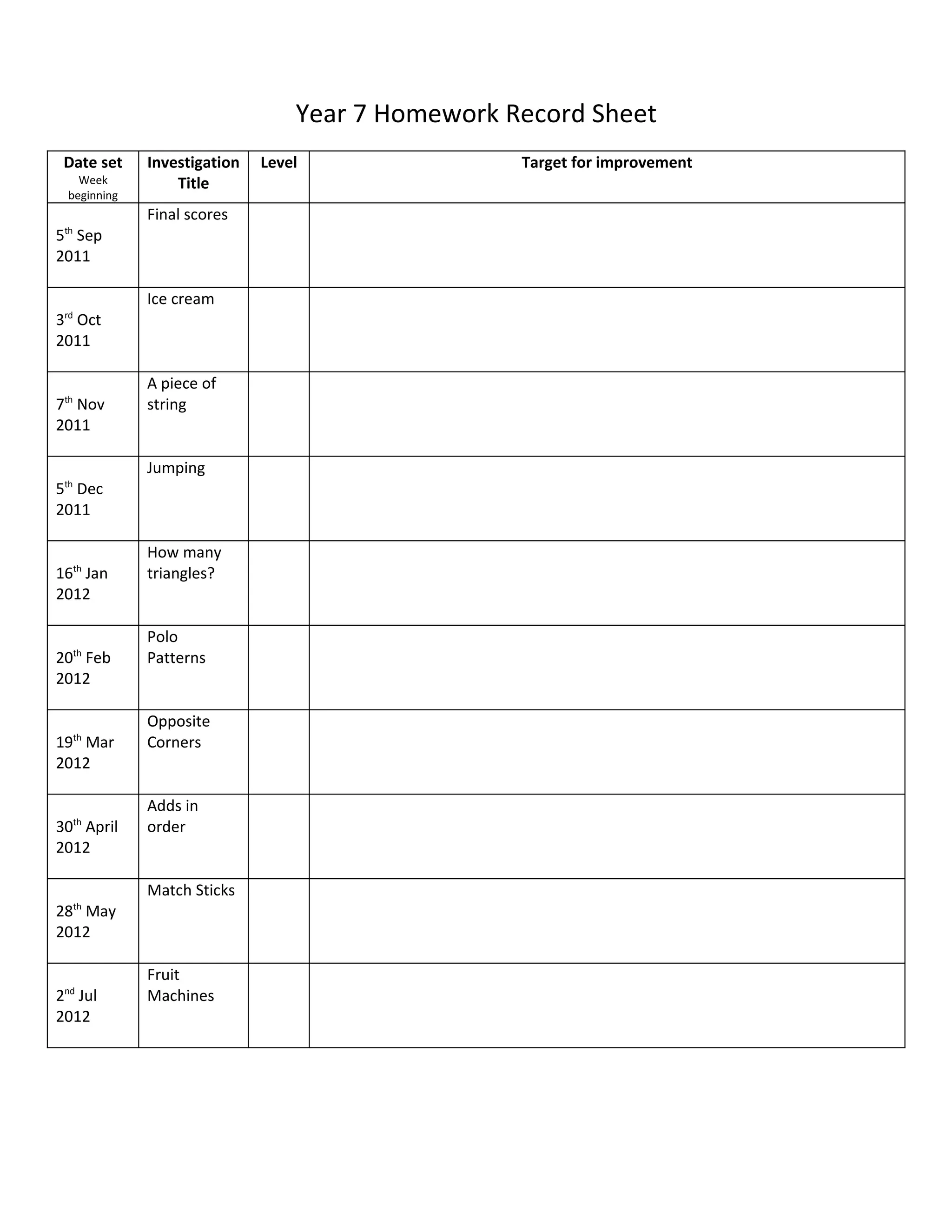
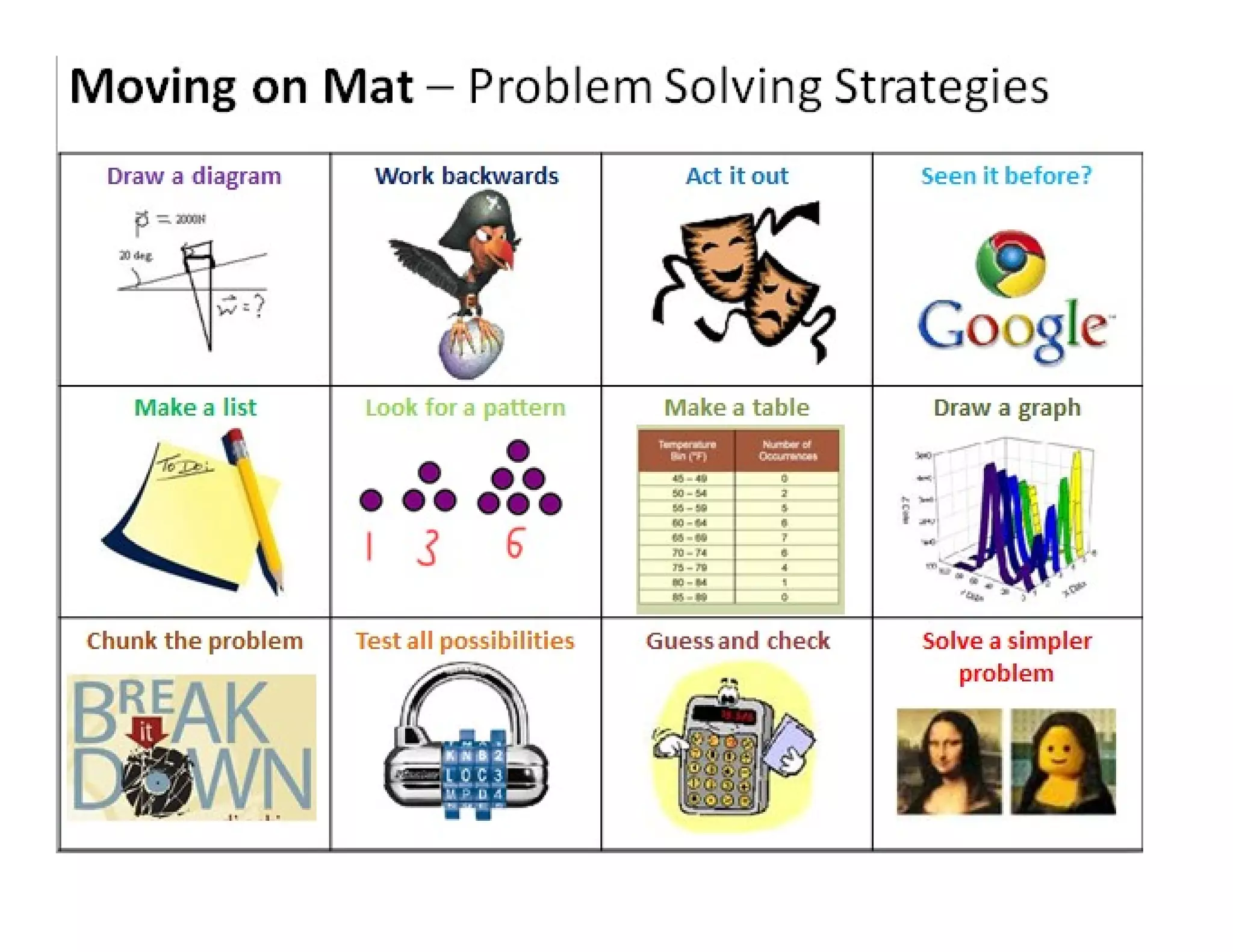
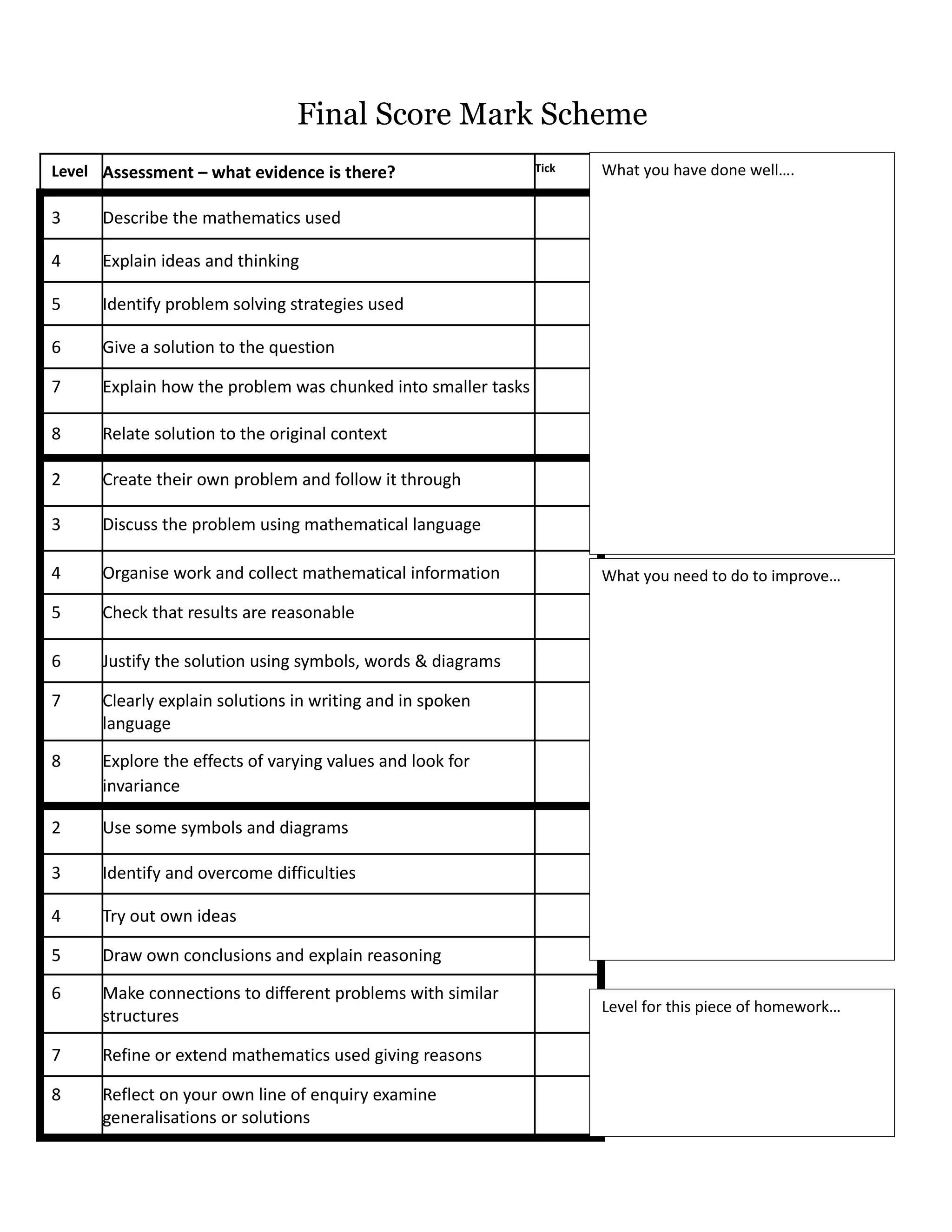
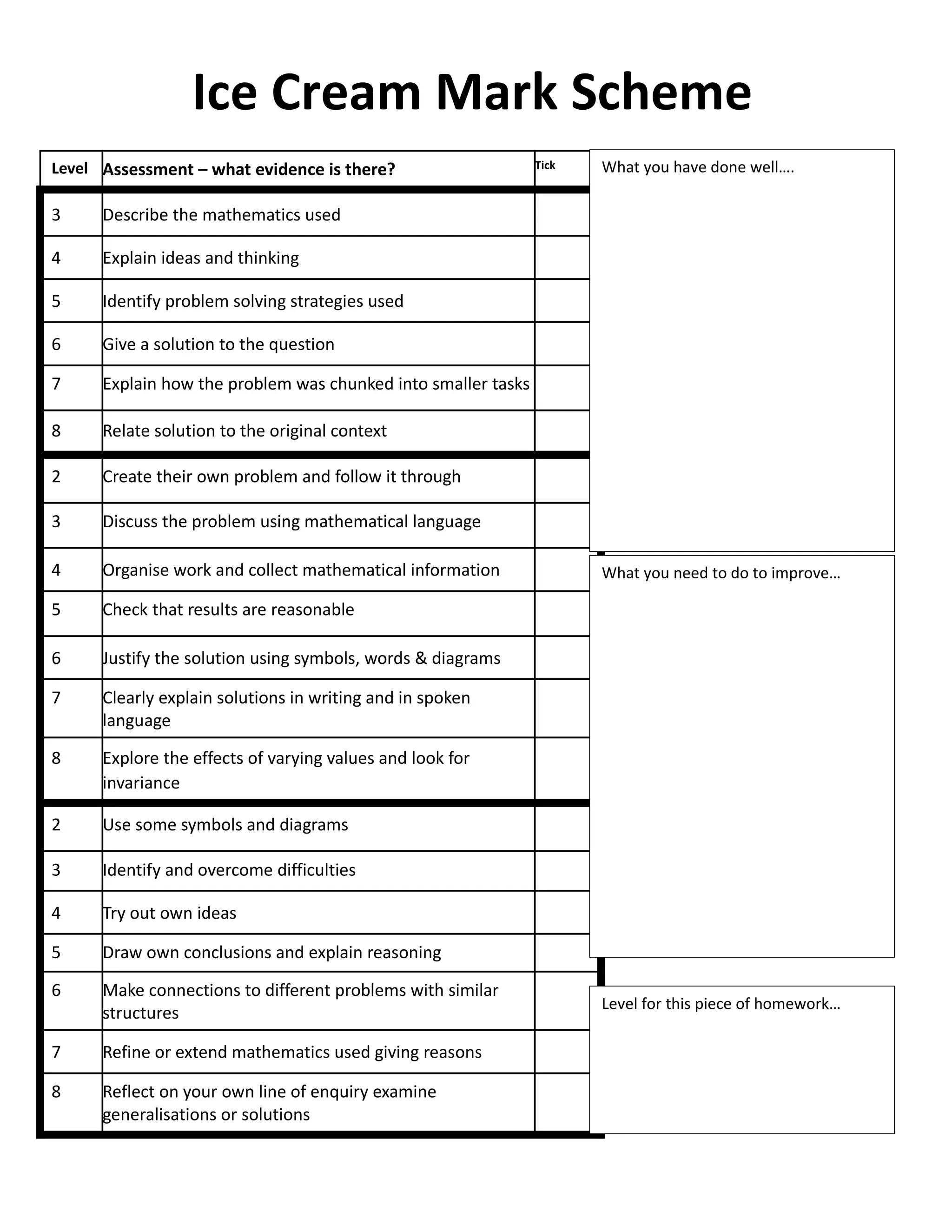
This document outlines an investigation homework assignment for year 7 students. It provides details on the structure and expectations of investigation homework throughout the school year. Students are expected to complete a minimum of 4 hours of work for each investigation, set in week A and due in week B. They must complete a poster or report for each investigation and have a target for improvement. The document provides an outline of investigation titles and due dates for the entire school year. It also includes guidance on how to approach investigations through various stages and problem solving strategies.

1. Year 7 Investigation Homework
Each investigation is designed to take a minimum of 4 hours and should be extended as much as the pupil is able. The
project should be set in the 1st lesson of week A and collected in at the end of week B. It is the expectation that for each
investigation a student completes a poster or report. The work produced should be levelled and the students should
have a target for improvement that they copy onto the homework record sheet (which is to be kept in the APP folder).
Outline for the year:
Date set Investigation Title Minimum Hours Due in
Week beginning Week beginning
5th Sep 2011 Final scores 4 hours 26th Sep 2011
3rd Oct Ice cream 4 hours 4th Nov 2011
2011
7th Nov A piece of string 4 hours 28th Nov 2011
2011
5th Dec Jumping 4 hours 9th Jan 2012
2011
16th Jan How many triangles? 4 hours 10th Feb 2012
2012
20th Feb Polo Patterns 4 hours 12th Mar 2012
2012
19th Mar Opposite Corners 4 hours 23rd April 2012
2012
30th April Adds in Order 4 hours 21st May 2012
2012
28th May Match Sticks 4 hours 25th June 2012
2012
2nd Jul Fruit Machine 4 hours 16th July 2012
2012

2. Year 7 Homework Record Sheet
Date set Investigation Level Target for improvement
Week Title
beginning
Final scores
5th Sep
2011
Ice cream
rd
3 Oct
2011
A piece of
7th Nov string
2011
Jumping
5th Dec
2011
How many
16th Jan triangles?
2012
Polo
20th Feb Patterns
2012
Opposite
th
19 Mar Corners
2012
Adds in
30th April order
2012
Match Sticks
th
28 May
2012
Fruit
2nd Jul Machines
2012

3. Tackling investigations
What are investigations?
In an investigation you are given a starting point and you are expected to explore different avenues for yourself.
Usually, having done this, you will be able to make some general statements about the situation.
Stage 1 ~ Getting Started
Look at the information I have been given.
Follow the instructions.
Can I see a connection?
NOW LET’S BE MORE SYSTEMATIC!
Stage 2 ~ Getting some results systematically
Put your results in a table if it makes them easier to understand or clearer to see.
Stage 3 ~ Making some predictions
I wonder if this always works? Find out…
Stage 4 ~ Making some generalisations
Can I justify this?
Check that what you are saying works for all of them.
Stage 5 ~ Can we find a rule?
Let’s look at the results in another way.
Stage 6 ~ Extend the investigation.
What if you change some of the information you started with, ask your teacher if you are not sure how to extend the
investigation.
Remember your teachers at Queensbury are her to help, if
you get stuck at any stage, come and ask one of the Maths
teachers.

5. Final Score
When Spain played Belgium in the preliminary round of the men's hockey competition in the 2008
Olympics, the final score was 4−2.
What could the half time score have been?
Can you find all the possible half time scores?
How will you make sure you don't miss any out?
In the final of the men's hockey in the 2000 Olympics, the Netherlands played Korea. The final score
was a draw; 3−3 and they had to take penalties.
Can you find all the possible half time scores for this match?
Investigate different final scores. Is there a pattern?

6. Final Score Mark Scheme
Level Assessment – what evidence is there? Tick What you have done well….
3 Describe the mathematics used
4 Explain ideas and thinking
5 Identify problem solving strategies used
6 Give a solution to the question
7 Explain how the problem was chunked into smaller tasks
8 Relate solution to the original context
2 Create their own problem and follow it through
3 Discuss the problem using mathematical language
4 Organise work and collect mathematical information What you need to do to improve…
5 Check that results are reasonable
6 Justify the solution using symbols, words & diagrams
7 Clearly explain solutions in writing and in spoken
language
8 Explore the effects of varying values and look for
invariance
2 Use some symbols and diagrams
3 Identify and overcome difficulties
4 Try out own ideas
5 Draw own conclusions and explain reasoning
6 Make connections to different problems with similar
Level for this piece of homework…
structures
7 Refine or extend mathematics used giving reasons
8 Reflect on your own line of enquiry examine
generalisations or solutions

8. Ice Cream
∞ I have started an ice cream parlor.
∞ I am selling double scoop ice creams.
∞ At the moment I am selling 2 flavours, Vanilla and
Chocolate.
I can make the following ice creams:
Vanilla Chocolate Chocolate
+ + +
Vanilla Vanilla Chocolate
∞ Now you choose three flavours.
∞ Each ice cream has a double scoop.
∞ How many different ice creams can you make?
Extension
Suppose you choose 4 flavours or 5 or 6…
What if you sell triple scoops.
How many then???????

9. Investigate

10. Ice Cream Mark Scheme
Level Assessment – what evidence is there? Tick What you have done well….
3 Describe the mathematics used
4 Explain ideas and thinking
5 Identify problem solving strategies used
6 Give a solution to the question
7 Explain how the problem was chunked into smaller tasks
8 Relate solution to the original context
2 Create their own problem and follow it through
3 Discuss the problem using mathematical language
4 Organise work and collect mathematical information What you need to do to improve…
5 Check that results are reasonable
6 Justify the solution using symbols, words & diagrams
7 Clearly explain solutions in writing and in spoken
language
8 Explore the effects of varying values and look for
invariance
2 Use some symbols and diagrams
3 Identify and overcome difficulties
4 Try out own ideas
5 Draw own conclusions and explain reasoning
6 Make connections to different problems with similar
Level for this piece of homework…
structures
7 Refine or extend mathematics used giving reasons
8 Reflect on your own line of enquiry examine
generalisations or solutions

12. A piece of String
You have a piece of string 20cm long.
1) How many different rectangles can you make?
Here is one
9cm
1cm 1cm
9cm
(Check 1 + 9 + 1 + 9 = 20)
Draw each rectangle on squared paper to show your results.
2) I am going to calculate the area of the rectangle I have drawn.
Area = base x height so for the one above it is 1 x 9 = 9cm².
From the rectangle you’ve drawn, which rectangle has the biggest area?
What is the length and width of this rectangle?
Write a sentence to say which rectangle has the biggest area.
3) Now repeat the ‘problem’ but the piece of string is now 32xm long.

13. 4) Now the string is 40cm long.
5) Now the string is 60cm long.
6) Look at all your answers for the biggest area. What do you notice?
7) Investigate circles when using string of 20cm.
8) Look at your answers for the largest area for each string size. What do you
notice?

14. A piece of String Mark Scheme
Level Assessment – what evidence is there? Tick What you have done well….
3 Describe the mathematics used
4 Explain ideas and thinking
5 Identify problem solving strategies used
6 Give a solution to the question
7 Explain how the problem was chunked into smaller tasks
8 Relate solution to the original context
2 Create their own problem and follow it through
3 Discuss the problem using mathematical language
4 Organise work and collect mathematical information What you need to do to improve…
5 Check that results are reasonable
6 Justify the solution using symbols, words & diagrams
7 Clearly explain solutions in writing and in spoken
language
8 Explore the effects of varying values and look for
invariance
2 Use some symbols and diagrams
3 Identify and overcome difficulties
4 Try out own ideas
5 Draw own conclusions and explain reasoning
6 Make connections to different problems with similar
Level for this piece of homework…
structures
7 Refine or extend mathematics used giving reasons
8 Reflect on your own line of enquiry examine
generalisations or solutions

15. Jumping
Ben is hoping to enter the long jump at his school sports day.
One day I saw him manage quite a good jump.
However, after practicing several days a week he finds that he can jump half as far again as he did
before.
This last jump was 3 75 meters long.
So how long was the first jump that I saw?
Now Mia has been practicing for the high jump.
I saw that she managed a fairly good jump, but after training hard, she managed to jump half as
high again as she did before.
This last jump was 1 20 meters.
So how high was the first jump that I saw?
You should try a trial and improvement method and record you results in a table. Use a number
line to help you.
Please tell us how you worked these out.
Can you find any other ways of finding a solution?
Which way do you prefer? Why?

16. Jumping Mark Scheme
Level Assessment – what evidence is there? Tick What you have done well….
3 Describe the mathematics used
4 Explain ideas and thinking
5 Identify problem solving strategies used
6 Give a solution to the question
7 Explain how the problem was chunked into smaller tasks
8 Relate solution to the original context
2 Create their own problem and follow it through
3 Discuss the problem using mathematical language
4 Organise work and collect mathematical information What you need to do to improve…
5 Check that results are reasonable
6 Justify the solution using symbols, words & diagrams
7 Clearly explain solutions in writing and in spoken
language
8 Explore the effects of varying values and look for
invariance
2 Use some symbols and diagrams
3 Identify and overcome difficulties
4 Try out own ideas
5 Draw own conclusions and explain reasoning
6 Make connections to different problems with similar
Level for this piece of homework…
structures
7 Refine or extend mathematics used giving reasons
8 Reflect on your own line of enquiry examine
generalisations or solutions

17. How many triangles?
Look at the shape below, how many triangles can you see?
I can see 5. Am I correct or can you see more or less? Highlight all the triangles
you can see.
How many triangles can you see in the shape below?
Can you draw a triangle like the ones above that have over 20 but less than 150
triangles?
Try and draw it to show if it or is not possible.

18. How many triangles? Mark Scheme
Level Assessment – what evidence is there? Tick What you have done well….
3 Describe the mathematics used
4 Explain ideas and thinking
5 Identify problem solving strategies used
6 Give a solution to the question
7 Explain how the problem was chunked into smaller tasks
8 Relate solution to the original context
2 Create their own problem and follow it through
3 Discuss the problem using mathematical language
4 Organise work and collect mathematical information What you need to do to improve…
5 Check that results are reasonable
6 Justify the solution using symbols, words & diagrams
7 Clearly explain solutions in writing and in spoken
language
8 Explore the effects of varying values and look for
invariance
2 Use some symbols and diagrams
3 Identify and overcome difficulties
4 Try out own ideas
5 Draw own conclusions and explain reasoning
6 Make connections to different problems with similar
Level for this piece of homework…
structures
7 Refine or extend mathematics used giving reasons
8 Reflect on your own line of enquiry examine
generalisations or solutions

19. Polo Patterns
When the black tiles surround white tiles this is known as a polo
pattern.
You are a tile designer and you have been asked to design different polo
patterns (this is be made by surrounding white tiles with black tiles).
The drawing shows one white tile surrounded by 8 black tiles.
What different polo patterns can you make with 12 black tiles (you can
surround as many white tiles as you like)?
Investigate how the number of tiles in a polo pattern depends on the number of
white tiles.

20. Polo Patterns Mark Scheme
Level Assessment – what evidence is there? Tick What you have done well….
3 Describe the mathematics used
4 Explain ideas and thinking
5 Identify problem solving strategies used
6 Give a solution to the question
7 Explain how the problem was chunked into smaller tasks
8 Relate solution to the original context
2 Create their own problem and follow it through
3 Discuss the problem using mathematical language
4 Organise work and collect mathematical information What you need to do to improve…
5 Check that results are reasonable
6 Justify the solution using symbols, words & diagrams
7 Clearly explain solutions in writing and in spoken
language
8 Explore the effects of varying values and look for
invariance
2 Use some symbols and diagrams
3 Identify and overcome difficulties
4 Try out own ideas
5 Draw own conclusions and explain reasoning
6 Make connections to different problems with similar
Level for this piece of homework…
structures
7 Refine or extend mathematics used giving reasons
8 Reflect on your own line of enquiry examine
generalisations or solutions

21. Opposite Corners.
1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100
The diagram shows a 100 square.
A rectangle has been shaded on the 100 square.
The numbers in the opposite corners of the shaded rectangle are
54 and 66 and 64 and 56
The products of the numbers in these opposite corners are
54 x 66 = 3564 and
64 x 56 = 3584
The difference between these products is 3584 – 3564 = 20
Task: Investigate the difference between the products of the numbers in the opposite corners
of any rectangles that can be drawn on a 100 square.

22. 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20 11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30 21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40 31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50 41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60 51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70 61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80 71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90 81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100 91 92 93 94 95 96 97 98 99 100
1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10
11 12 13 14 15 16 17 18 19 20 11 12 13 14 15 16 17 18 19 20
21 22 23 24 25 26 27 28 29 30 21 22 23 24 25 26 27 28 29 30
31 32 33 34 35 36 37 38 39 40 31 32 33 34 35 36 37 38 39 40
41 42 43 44 45 46 47 48 49 50 41 42 43 44 45 46 47 48 49 50
51 52 53 54 55 56 57 58 59 60 51 52 53 54 55 56 57 58 59 60
61 62 63 64 65 66 67 68 69 70 61 62 63 64 65 66 67 68 69 70
71 72 73 74 75 76 77 78 79 80 71 72 73 74 75 76 77 78 79 80
81 82 83 84 85 86 87 88 89 90 81 82 83 84 85 86 87 88 89 90
91 92 93 94 95 96 97 98 99 100 91 92 93 94 95 96 97 98 99 100

23. Opposite Corners Mark Scheme
Level Assessment – what evidence is there? Tick What you have done well….
3 Describe the mathematics used
4 Explain ideas and thinking
5 Identify problem solving strategies used
6 Give a solution to the question
7 Explain how the problem was chunked into smaller tasks
8 Relate solution to the original context
2 Create their own problem and follow it through
3 Discuss the problem using mathematical language
4 Organise work and collect mathematical information What you need to do to improve…
5 Check that results are reasonable
6 Justify the solution using symbols, words & diagrams
7 Clearly explain solutions in writing and in spoken
language
8 Explore the effects of varying values and look for
invariance
2 Use some symbols and diagrams
3 Identify and overcome difficulties
4 Try out own ideas
5 Draw own conclusions and explain reasoning
6 Make connections to different problems with similar
Level for this piece of homework…
structures
7 Refine or extend mathematics used giving reasons
8 Reflect on your own line of enquiry examine
generalisations or solutions

24. Numbers in order like 7, 8, 9 are called CONSECUTIVE numbers.
4+5=9
12 = 3 + 4 +
6=1+
5
17 = 8 + 9 2+3
17, 9, 6 and 12 have all been made by adding CONSECUTIVE numbers.
What other numbers can you make in this way? Why?
Are there any numbers that you cannot make? Why?

25. Adds in Order Mark Scheme
Level Assessment – what evidence is there? Tick What you have done well….
3 Describe the mathematics used
4 Explain ideas and thinking
5 Identify problem solving strategies used
6 Give a solution to the question
7 Explain how the problem was chunked into smaller tasks
8 Relate solution to the original context
2 Create their own problem and follow it through
3 Discuss the problem using mathematical language
4 Organise work and collect mathematical information What you need to do to improve…
5 Check that results are reasonable
6 Justify the solution using symbols, words & diagrams
7 Clearly explain solutions in writing and in spoken
language
8 Explore the effects of varying values and look for
invariance
2 Use some symbols and diagrams
3 Identify and overcome difficulties
4 Try out own ideas
5 Draw own conclusions and explain reasoning
6 Make connections to different problems with similar
Level for this piece of homework…
structures
7 Refine or extend mathematics used giving reasons
8 Reflect on your own line of enquiry examine
generalisations or solutions

26. Match Sticks
Look at the match stick shape below.
How many match sticks do you expect to be in pattern 2?
Pattern 2 Pattern 3
2 triangles 3 triangles
Draw the next 5 patterns.
What do you notice about the number of matchsticks used, is there a pattern?
Extension - Can you write it in algebra?
How many matchsticks do you need to make the 50th pattern?
What’s the biggest number pattern can you make with 100 matchsticks? Are there
any left over?
Think about different shapes you can make using matchsticks, investigate (as
above).

27. Match Sticks Mark Scheme
Level Assessment – what evidence is there? Tick What you have done well….
3 Describe the mathematics used
4 Explain ideas and thinking
5 Identify problem solving strategies used
6 Give a solution to the question
7 Explain how the problem was chunked into smaller tasks
8 Relate solution to the original context
2 Create their own problem and follow it through
3 Discuss the problem using mathematical language
4 Organise work and collect mathematical information What you need to do to improve…
5 Check that results are reasonable
6 Justify the solution using symbols, words & diagrams
7 Clearly explain solutions in writing and in spoken
language
8 Explore the effects of varying values and look for
invariance
2 Use some symbols and diagrams
3 Identify and overcome difficulties
4 Try out own ideas
5 Draw own conclusions and explain reasoning
6 Make connections to different problems with similar
Level for this piece of homework…
structures
7 Refine or extend mathematics used giving reasons
8 Reflect on your own line of enquiry examine
generalisations or solutions
Fruit Machine
In this task you are going to design your own fruit machine.

28. Start with a simple one so you can see how it works.
Use two strips for the reels – each reel has three fruits.
Lemon
Banana
Apple
The only way to win on this machine is to get two apples. If you win you get 50 pence back. It costs 10
pence to play.
Is it worth playing?
You need to know how many different combinations of fruits you can get.
Use the worksheet. Carefully cut out two strips and the slotted fruit machine. Fit the strips into the
first two reels of the machine. Start with lemons in both windows. Move reel 2 one space up – now you
have a lemon and an apple. Try to work logically, and record all the possible combinations in a table,
starting like this:
Reel 1 Reel 2
How many different ways can the machine stop? Are you likely to win?
Lemon Lemon Is it worth playing?
Lemon Apple
Lemon

29. .
Maths Fruit Machine
Cut out this window Cut out this window
Only 10 pence per play.
Match two apples to win 50 pence.

30. Fruit Machine Mark Scheme
Level Assessment – what evidence is there? Tick What you have done well….
3 Describe the mathematics used
4 Explain ideas and thinking
5 Identify problem solving strategies used
6 Give a solution to the question
7 Explain how the problem was chunked into smaller tasks
8 Relate solution to the original context
2 Create their own problem and follow it through
3 Discuss the problem using mathematical language
4 Organise work and collect mathematical information What you need to do to improve…
5 Check that results are reasonable
6 Justify the solution using symbols, words & diagrams
7 Clearly explain solutions in writing and in spoken
language
8 Explore the effects of varying values and look for
invariance
2 Use some symbols and diagrams
3 Identify and overcome difficulties
4 Try out own ideas
5 Draw own conclusions and explain reasoning
6 Make connections to different problems with similar
Level for this piece of homework…
structures
7 Refine or extend mathematics used giving reasons
8 Reflect on your own line of enquiry examine
generalisations or solutions