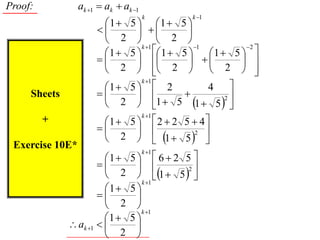
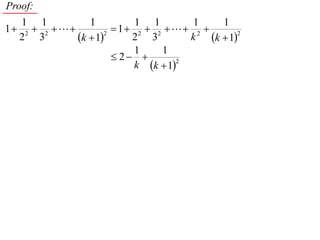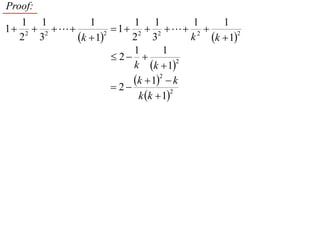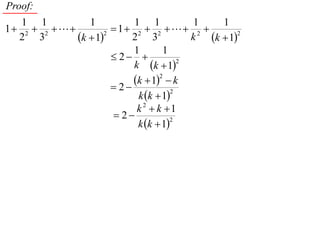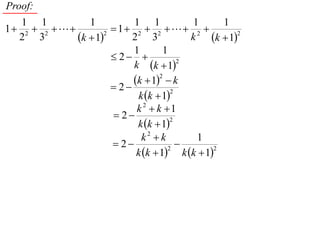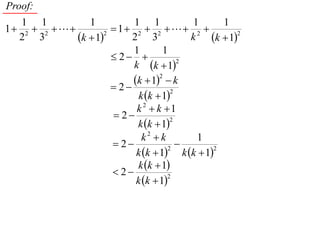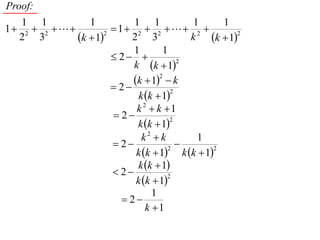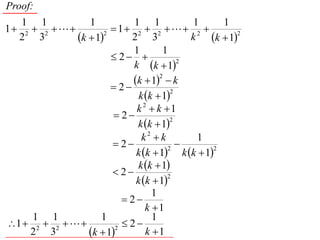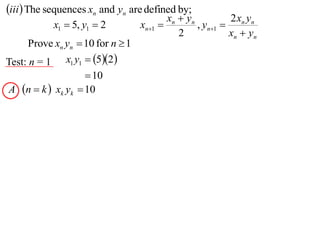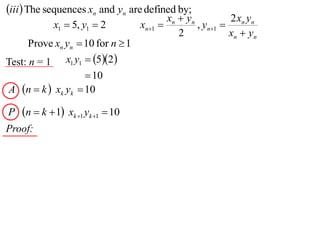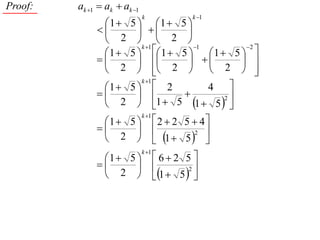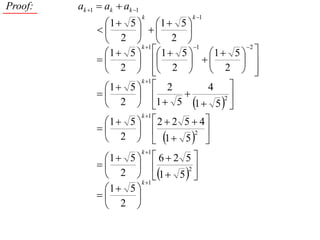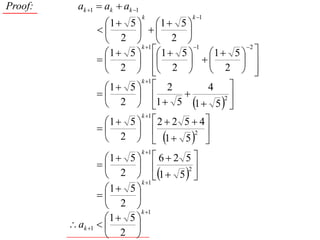The document discusses mathematical induction. It first proves that the sum of the series from 1/2 to 1/n is less than or equal to 2 - 1/n. It then proves by induction that for a sequence defined by a1 = 2 and an+1 = 2 + an, an is always less than 2 for n ≥ 1.

1. Mathematical Induction

2. Mathematical Induction
1 1 1 1
e.g. i  Prove 1  2  2    2  2 
2 3 n n

3. Mathematical Induction
1 1 1 1
e.g. i  Prove 1  2  2    2  2 
2 3 n n
Test: n = 1

4. Mathematical Induction
1 1 1 1
e.g. i  Prove 1  2  2    2  2 
2 3 n n
1
Test: n = 1 L.H .S  2
1
1

5. Mathematical Induction
1 1 1 1
e.g. i  Prove 1  2  2    2  2 
2 3 n n
1 1
Test: n = 1 L.H .S  2 R.H .S  2 
1 1
1 1

6. Mathematical Induction
1 1 1 1
e.g. i  Prove 1  2  2    2  2 
2 3 n n
1 1
Test: n = 1 L.H .S  2 R.H .S  2 
1 1
1 1
 L.H .S  R.H .S

7. Mathematical Induction
1 1 1 1
e.g. i  Prove 1  2  2    2  2 
2 3 n n
1 1
Test: n = 1 L.H .S  2 R.H .S  2 
1 1
1 1
 L.H .S  R.H .S
1 1 1 1
A n  k  1  2  2    2  2 
2 3 k k

8. Mathematical Induction
1 1 1 1
e.g. i  Prove 1  2  2    2  2 
2 3 n n
1 1
Test: n = 1 L.H .S  2 R.H .S  2 
1 1
1 1
 L.H .S  R.H .S
1 1 1 1
A n  k  1  2  2    2  2 
2 3 k k
1 1 1 1
P n  k  1 1  2  2     2
2 3 k  12
k 1

9. Proof:
1 1 1 1 1 1 1
1 2  2   1 2  2  2 
2 3 k  12
2 3 k k  12

10. Proof:
1 1 1 1 1 1 1
1 2  2   1 2  2  2 
2 3 k  12
2 3 k k  12
1 1
 2 
k k  12

11. Proof:
1 1 1 1 1 1 1
1 2  2   1 2  2  2 
2 3 k  12
2 3 k k  12
1 1
 2 
k k  12
k  1  k
2
 2
k k  1
2

12. Proof:
1 1 1 1 1 1 1
1 2  2   1 2  2  2 
2 3 k  12
2 3 k k  12
1 1
 2 
k k  12
k  1  k
2
 2
k k  1
2
k 2  k 1
 2
k k  1
2

13. Proof:
1 1 1 1 1 1 1
1 2  2   1 2  2  2 
2 3 k  12
2 3 k k  12
1 1
 2 
k k  12
k  1  k
2
 2
k k  1
2
k 2  k 1
 2
k k  1
2
k2  k 1
 2 
k k  1 k k  1
2 2

14. Proof:
1 1 1 1 1 1 1
1 2  2   1 2  2  2 
2 3 k  12
2 3 k k  12
1 1
 2 
k k  12
k  1  k
2
 2
k k  1
2
k 2  k 1
 2
k k  1
2
k2  k 1
 2 
k k  1 k k  1
2 2
k k  1
 2
k k  1
2

15. Proof:
1 1 1 1 1 1 1
1 2  2   1 2  2  2 
2 3 k  12
2 3 k k  12
1 1
 2 
k k  12
k  1  k
2
 2
k k  1
2
k 2  k 1
 2
k k  1
2
k2  k 1
 2 
k k  1 k k  1
2 2
k k  1
 2
k k  1
2
1
 2
k 1

16. Proof:
1 1 1 1 1 1 1
1 2  2   1 2  2  2 
2 3 k  12
2 3 k k  12
1 1
 2 
k k  12
k  1  k
2
 2
k k  1
2
k 2  k 1
 2
k k  1
2
k2  k 1
 2 
k k  1 k k  1
2 2
k k  1
 2
k k  1
2
1
 2
k 1
1 1 1 1
1  2  2     2
2 3 k  12
k 1

17. (ii) A sequence is defined by;
a1  2 an1  2  an for n  1
Show that an  2 for n  1

18. (ii) A sequence is defined by;
a1  2 an1  2  an for n  1
Show that an  2 for n  1
Test: n = 1

19. (ii) A sequence is defined by;
a1  2 an1  2  an for n  1
Show that an  2 for n  1
Test: n = 1 a1  2  2

20. (ii) A sequence is defined by;
a1  2 an1  2  an for n  1
Show that an  2 for n  1
Test: n = 1 a1  2  2
A n  k  ak  2

21. (ii) A sequence is defined by;
a1  2 an1  2  an for n  1
Show that an  2 for n  1
Test: n = 1 a1  2  2
A n  k  ak  2
P n  k  1 ak 1  2

22. (ii) A sequence is defined by;
a1  2 an1  2  an for n  1
Show that an  2 for n  1
Test: n = 1 a1  2  2
A n  k  ak  2
P n  k  1 ak 1  2
Proof:

23. (ii) A sequence is defined by;
a1  2 an1  2  an for n  1
Show that an  2 for n  1
Test: n = 1 a1  2  2
A n  k  ak  2
P n  k  1 ak 1  2
Proof:
ak 1  2  ak

24. (ii) A sequence is defined by;
a1  2 an1  2  an for n  1
Show that an  2 for n  1
Test: n = 1 a1  2  2
A n  k  ak  2
P n  k  1 ak 1  2
Proof:
ak 1  2  ak
 22

25. (ii) A sequence is defined by;
a1  2 an1  2  an for n  1
Show that an  2 for n  1
Test: n = 1 a1  2  2
A n  k  ak  2
P n  k  1 ak 1  2
Proof:
ak 1  2  ak
 22
 4
2

26. (ii) A sequence is defined by;
a1  2 an1  2  an for n  1
Show that an  2 for n  1
Test: n = 1 a1  2  2
A n  k  ak  2
P n  k  1 ak 1  2
Proof:
ak 1  2  ak
 22
 4
2
 ak 1  2

27. iii The sequences xn and yn are defined by;
xn  yn 2x y
x1  5, y1  2 xn1  , yn1  n n
2 xn  yn
Prove xn yn  10 for n  1

28. iii The sequences xn and yn are defined by;
xn  yn 2x y
x1  5, y1  2 xn1  , yn1  n n
2 xn  yn
Prove xn yn  10 for n  1
Test: n = 1

29. iii The sequences xn and yn are defined by;
xn  yn 2x y
x1  5, y1  2 xn1  , yn1  n n
2 xn  yn
Prove xn yn  10 for n  1
Test: n = 1 x1 y1  52
 10

30. iii The sequences xn and yn are defined by;
xn  yn 2x y
x1  5, y1  2 xn1  , yn1  n n
2 xn  yn
Prove xn yn  10 for n  1
Test: n = 1 x1 y1  52
 10
A n  k  xk yk  10

31. iii The sequences xn and yn are defined by;
xn  yn 2x y
x1  5, y1  2 xn1  , yn1  n n
2 xn  yn
Prove xn yn  10 for n  1
Test: n = 1 x1 y1  52
 10
A n  k  xk yk  10
P n  k  1 xk 1 yk 1  10

32. iii The sequences xn and yn are defined by;
xn  yn 2x y
x1  5, y1  2 xn1  , yn1  n n
2 xn  yn
Prove xn yn  10 for n  1
Test: n = 1 x1 y1  52
 10
A n  k  xk yk  10
P n  k  1 xk 1 yk 1  10
Proof:

33. iii The sequences xn and yn are defined by;
xn  yn 2x y
x1  5, y1  2 xn1  , yn1  n n
2 xn  yn
Prove xn yn  10 for n  1
Test: n = 1 x1 y1  52
 10
A n  k  xk yk  10
P n  k  1 xk 1 yk 1  10
Proof:
 xk  yk  2 xk yk 
xk 1 yk 1   
x  y  
 2  k k 

34. iii The sequences xn and yn are defined by;
xn  yn 2x y
x1  5, y1  2 xn1  , yn1  n n
2 xn  yn
Prove xn yn  10 for n  1
Test: n = 1 x1 y1  52
 10
A n  k  xk yk  10
P n  k  1 xk 1 yk 1  10
Proof:
 xk  yk  2 xk yk 
xk 1 yk 1   
x  y  
 2  k k 
 xk y k
 10

35. iii The sequences xn and yn are defined by;
xn  yn 2x y
x1  5, y1  2 xn1  , yn1  n n
2 xn  yn
Prove xn yn  10 for n  1
Test: n = 1 x1 y1  52
 10
A n  k  xk yk  10
P n  k  1 xk 1 yk 1  10
Proof:
 xk  yk  2 xk yk 
xk 1 yk 1   
x  y  
 2  k k 
 xk y k
 10
 xk 1 yk 1  10

36. (iv) The Fibonacci sequence is defined by;
a1  a2  1 an1  an  an1 for n  1
n
1  5 
Prove that an    for n  1
 2 

37. (iv) The Fibonacci sequence is defined by;
a1  a2  1 an1  an  an1 for n  1
n
1  5 
Prove that an    for n  1
 2 
Test: n = 1 and n =2

38. (iv) The Fibonacci sequence is defined by;
a1  a2  1 an1  an  an1 for n  1
n
1  5 
Prove that an    for n  1
 2 
Test: n = 1 and n =2
L.H .S  a1
1

39. (iv) The Fibonacci sequence is defined by;
a1  a2  1 an1  an  an1 for n  1
n
1  5 
Prove that an    for n  1
 2 
Test: n = 1 and n =2 1
1  5 
L.H .S  a1 R.H .S   
 2 
1
 1.62

40. (iv) The Fibonacci sequence is defined by;
a1  a2  1 an1  an  an1 for n  1
n
1  5 
Prove that an    for n  1
 2 
Test: n = 1 and n =2 1
1  5 
L.H .S  a1 R.H .S   
 2 
1
 1.62
 L.H .S  R.H .S

41. (iv) The Fibonacci sequence is defined by;
a1  a2  1 an1  an  an1 for n  1
n
1  5 
Prove that an    for n  1
 2 
Test: n = 1 and n =2 1
1  5 
L.H .S  a1 R.H .S   
 2 
1
 1.62
 L.H .S  R.H .S
L.H .S  a2
1

42. (iv) The Fibonacci sequence is defined by;
a1  a2  1 an1  an  an1 for n  1
n
1  5 
Prove that an    for n  1
 2 
Test: n = 1 and n =2 1
1  5 
L.H .S  a1 R.H .S   
 2 
1
 1.62
 L.H .S  R.H .S 2
1  5 
L.H .S  a2 R.H .S   
 2 
1
 2.62

43. (iv) The Fibonacci sequence is defined by;
a1  a2  1 an1  an  an1 for n  1
n
1  5 
Prove that an    for n  1
 2 
Test: n = 1 and n =2 1
1  5 
L.H .S  a1 R.H .S   
 2 
1
 1.62
 L.H .S  R.H .S 2
1  5 
L.H .S  a2 R.H .S   
 2 
1
 2.62
 L.H .S  R.H .S

44. (iv) The Fibonacci sequence is defined by;
a1  a2  1 an1  an  an1 for n  1
n
1  5 
Prove that an    for n  1
 2 
Test: n = 1 and n =2 1
1  5 
L.H .S  a1 R.H .S   
 2 
1
 1.62
 L.H .S  R.H .S 2
1  5 
L.H .S  a2 R.H .S   
 2 
1
 2.62
 L.H .S  R.H .S
k 1 k
1  5  1  5 
A n  k  1 & n  k  ak 1    & ak   
 2   2 

45. (iv) The Fibonacci sequence is defined by;
a1  a2  1 an1  an  an1 for n  1
n
1  5 
Prove that an    for n  1
 2 
Test: n = 1 and n =2 1
1  5 
L.H .S  a1 R.H .S   
 2 
1
 1.62
 L.H .S  R.H .S 2
1  5 
L.H .S  a2 R.H .S   
 2 
1
 2.62
 L.H .S  R.H .S
k 1 k
1  5  1  5 
A n  k  1 & n  k  ak 1    & ak   
 2   2 
k 1
1  5 
P n  k  1 ak 1   
 2 

46. Proof: ak 1  ak  ak 1

47. Proof: ak 1  ak  ak 1
k k 1
1  5  1  5 
   
 2   2 

48. Proof: ak 1  ak  ak 1
k k 1
1  5  1  5
   
 2   2 
k 1 1 2
 1  5   1  5 1  5  
      
 2   2    2   

49. Proof: ak 1  ak  ak 1
k k 1
1  5  1 5
   
 2   2 
k 1 1 2
 1  5   1 
5 1  5  
      
 2   2 
  2   
k 1
1  5   2 4 
    2
 2  1  5 1  5  

50. Proof: ak 1  ak  ak 1
k k 1
1  5  1  5
   
 2   2 
k 1 1 2
 1  5   1  5 1  5  
      
 2   2    2   
k 1
1  5  2 4 
    2
 2  1  5 1  5  
k 1
1  5  2  2 5  4
   2 
 2   1  5  
k 1
1  5  62 5 
   2
 2   1  5  

51. Proof: ak 1  ak  ak 1
k k 1
1  5  1  5
   
 2   2 
k 1 1 2
 1  5   1  5 1  5  
      
 2   2    2   
k 1
1  5  2 4 
    2
 2  1  5 1  5  
k 1
1  5  2  2 5  4
   2 
 2   1  5  
k 1
1  5   6  2 5 
   
 2   1  5 2 
k 1
1  5 
 
 2 

52. Proof: ak 1  ak  ak 1
k k 1
1  5  1  5
   
 2   2 
k 1 1 2
 1  5   1  5 1  5  
      
 2   2    2   
k 1
1  5  2 4 
    2
 2  1  5 1  5  
k 1
1  5  2  2 5  4
   2 
 2   1  5  
k 1
1  5   6  2 5 
   
 2   1  5 2 
k 1
1  5 
 
 2 
k 1
1  5 
 ak 1   
 2 

53. Proof: ak 1  ak  ak 1
k k 1
1  5  1  5
   
 2   2 
k 1 1 2
 1  5   1  5 1  5  
      
 2   2    2   
k 1
1  5  2 4 
Sheets     2
 2  1  5 1  5  
k 1
+ 1  5  2  2 5  4
   2 
 2   1  5  
Exercise 10E*
k 1
1  5   6  2 5 
   
 2   1  5 2 
k 1
1  5 
 
 2 
k 1
1  5 
 ak 1   
 2 