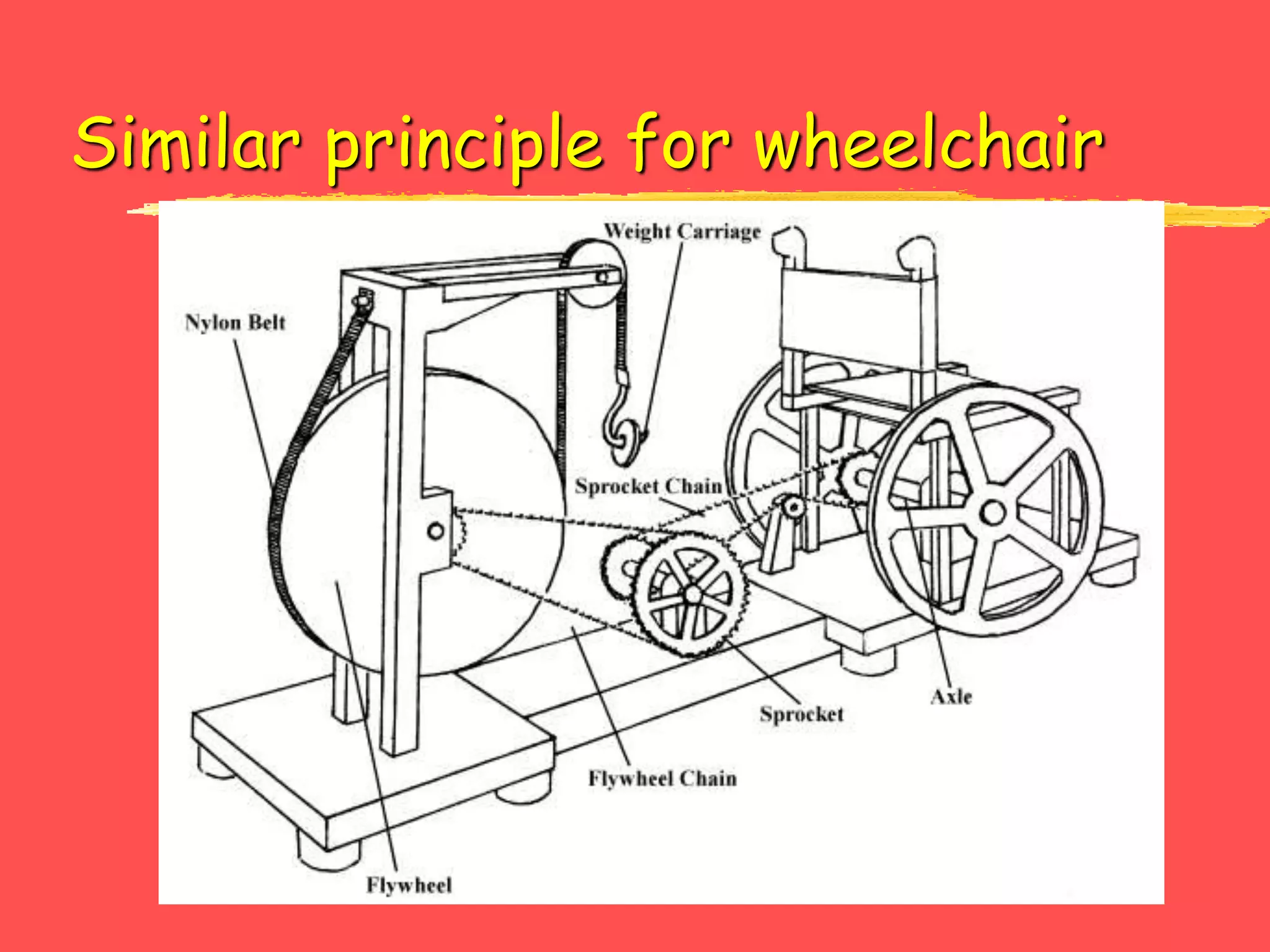
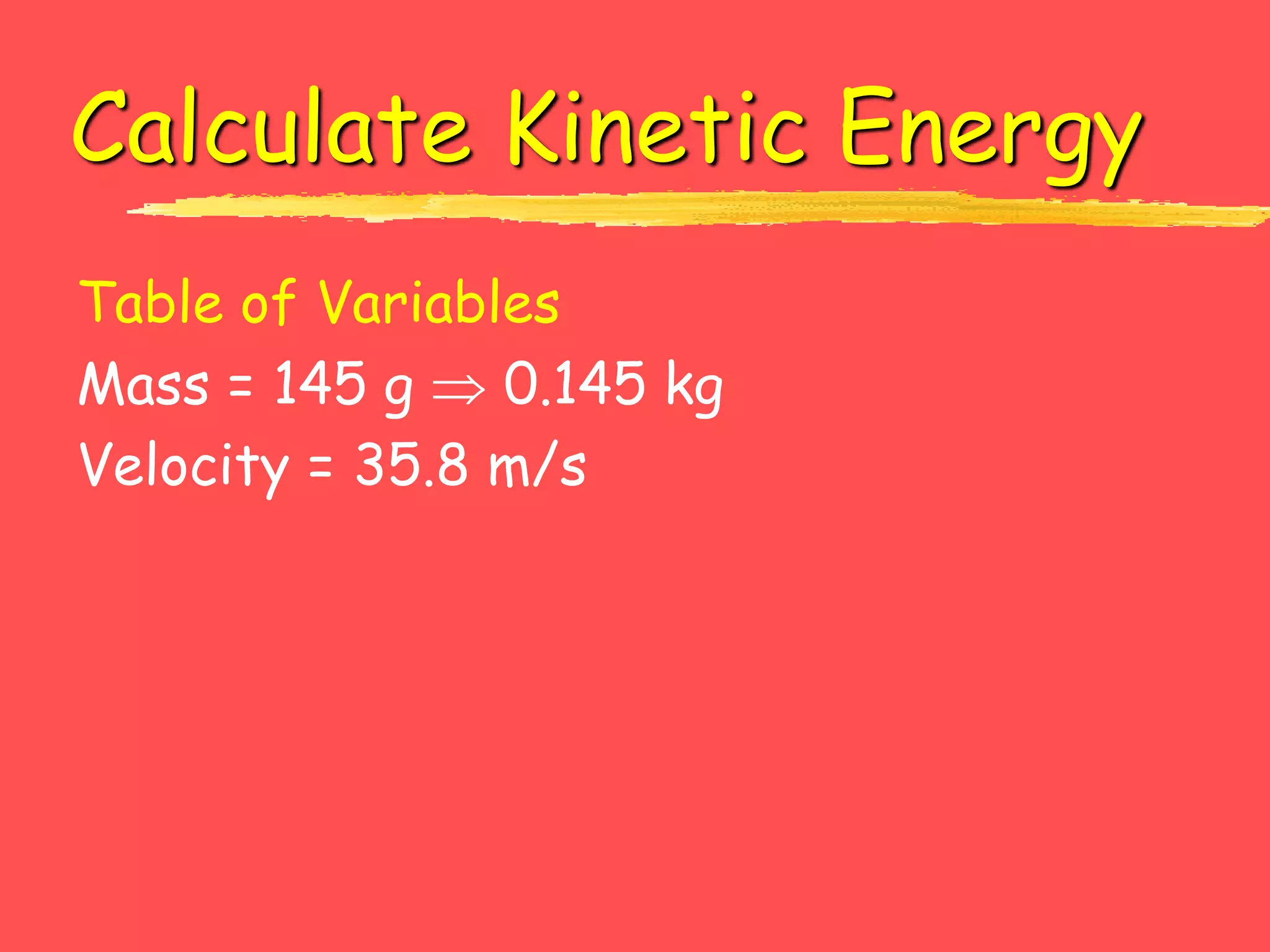
1. Work is the product of the applied force and the displacement along the line of action of the force. Positive work is done when force and displacement are in the same direction, while negative work is done when they are in opposite directions. 2. Kinetic energy is the energy of motion and is calculated as one-half mass times velocity squared. Potential energy is the energy due to an object's position or deformation and includes gravitational potential energy calculated as mass times gravitational field strength times height, and strain potential energy stored in deformed objects. 3. The work-energy principle states that the work done on an object causes a change in its kinetic and potential energies. Work can convert an object's potential energy to

1. Work, Power & Energy
Explaining the Causes of
Motion in a Different Way

2. Work
The product of force and the amount of
displacement along the line of action of
that force.
Units: Newton•meter (Joule)
ft . lbs (horsepower)
nt
displaceme
Force
Work 


3. Work = F x d
To calculate work done on an object, we
need:
The Force
The average magnitude of the force
The direction of the force
The Displacement
The magnitude of the change of position
The direction of the change of position

4. Calculate Work
During the ascent phase of a rep of the
bench press, the lifter exerts an
average vertical force of 1000 N
against a barbell while the barbell
moves 0.8 m upward
How much work did the lifter do to the
barbell?

5. Calculate Work
Table of Variables:
Force = +1000 N
Displacement = +0.8 m
Force is positive due to pushing upward
Displacement is positive due to moving
upward

6. Calculate Work
Table of Variables:
Force = +1000 N
Displacement = +0.8 m
Select the equation and solve:
   
J
Joule
Nm
Work
m
N
Work
nt
displaceme
Force
Work
800
800
800
8
.
0
1000










7. - & + Work
Positive work is performed when
the direction of the force and
the direction of motion are the
same
ascent phase of the bench press
Throwing a ball
push off (upward) phase of a jump

8. Calculate Work
During the descent phase of a rep of
the bench press, the lifter exerts an
average vertical force of 1000 N
against a barbell while the barbell
moves 0.8 m downward

9. Calculate Work
Table of Variables
Force = +1000 N
Displacement = -0.8 m
Force is positive due to pushing upward
Displacement is negative due to movement
downward

10. Calculate Work
Table of Variables
Force = +1000 N
Displacement = -0.8 m
Select the equation and solve:
   
J
Joule
Nm
Work
m
N
Work
nt
displaceme
Force
Work
800
800
800
8
.
0
1000













11. - & + Work
Positive work
Negative work is performed
when the direction of the force
and the direction of motion are
the opposite
descent phase of the bench press
catching
landing phase of a jump

12. Work performed climbing
stairs
 Work = Fd
 Force
 Subject weight
 From mass, ie 65 kg
 Displacement
 Height of each step
 Typical 8 inches (20cm)
 Work per step
 650N x 0.2 m = 130.0 Nm
 Multiply by the number of steps

13. Work on a stair stepper
Work = Fd
Force
Push on the step
????
Displacement
Step Height
8 inches
“Work” per step
???N x .203 m = ???Nm

14. Work on a cycle ergometer
Work = Fd
Force
belt friction on the flywheel
mass (eg 3 kg)
Displacement
revolution of the pedals
Monark: 6 m
“Work” per revolution

15. Work on a cycle ergometer
 Work = Fd
 Force
 belt friction on the flywheel
 mass (eg 3 kg)
 Displacement
 revolution of the pedals
 Monark: 6 m
 “Work” per revolution
 3kg x 6 m = 18 kgm

16. Similar principle for wheelchair

17. …and for handcycling
ergometer

18. Power
The rate of doing work
Work = Fd
Units: Fd/s = J/s = watt
velocity
Force
Power
t
Fd
Power
time
Work
Power




/
/

19. Calculate & compare power
During the ascent phase of a rep of the
bench press, two lifters each exert an
average vertical force of 1000 N
against a barbell while the barbell
moves 0.8 m upward
Lifter A: 0.50 seconds
Lifter B: 0.75 seconds

20. Calculate & compare power
Lifter A
Table of Variables
F = 1000 N
d = 0.8 m
t = 0.50 s
Lifter B’s time would
be .75 sec instead
of .5 sec
w
s
J
Power
s
m
N
Power
t
Fd
Power
1600
50
.
0
800
50
.
0
8
.
0
1000






22. Energy
 Energy (E) is defined as the capacity to do
work (scalar)
 Many forms
No more created, only converted
 chemical, sound, heat, nuclear, mechanical
 Kinetic Energy (KE):
 energy due to motion
 Potential Energy (PE):
 energy due to position or deformation

23. Kinetic Energy
Energy due to motion reflects
the mass
the velocity of the object
KE = 1/2 mv2

24. Calculate Kinetic Energy
How much KE in a 5
ounce baseball (145 g)
thrown at 80 miles/hr
(35.8 m/s)?

25. Calculate Kinetic Energy
Table of Variables
Mass = 145 g  0.145 kg
Velocity = 35.8 m/s

26. Calculate Kinetic Energy
Table of Variables
Mass = 145 g  0.145 kg
Velocity = 35.8 m/s
Select the equation and solve:
KE = ½ m v2
KE = ½ (0.145 kg)(35.8 m/s)2
KE = ½ (0.145 kg)(1281.54 m/s/s)
KE = ½ (185.8 kg m/s/s)
KE = 92.9 kg m/s/s, or 92.9 Nm, or 92.9J

27. Calculate Kinetic Energy
How much KE possessed by
a 68.1 kg female volleyball
player moving downward at
3.2 m/s after a block?

28. Calculate Kinetic Energy
Table of Variables
 68.18 kg of mass
 -3.2 m/s
Select the equation and solve:
KE = ½ m v2
 KE = ½ (68.18 kg)(-3.2 m/s)2
 KE = ½ (68.18 kg)(10.24 m/s/s)
 KE = ½ (698.16 kg m/s/s)
 KE = 349.08 Nm or J

29. Calculate Kinetic Energy
Compare KE possessed by:
 a 220 pound (100 kg) running back
moving forward at 4.0 m/s
 a 385 pound (175 kg) lineman moving
forward at 3.75 m/s

30. Calculate Kinetic Energy
Table of Variables
m = 100 Kg
v = 4.0 m/s
Select the equation
and solve:
KE = ½ m v2
KE = ½ (100 kg)(4.0
m/s)2
KE = 800 Nm or J
Table of Variables
m = 175 kg
v = 3.75 m/s
Select the equation
and solve:
KE = ½ m v2
KE = ½ (175)(3.75)2
KE = 1230 Nm or J

31. Potential Energy
Two forms of PE:
Gravitational PE:
energy due to an object’s position
relative to the earth
Strain PE:
due to the deformation of an
object

32. Gravitational PE
Affected by the object’s
 weight
mg
elevation (height) above reference point
 ground or some other surface
h
GPE = mgh

33. Calculate GPE
How much gravitational potential energy
in a 45 kg gymnast when she is 4m
above the mat of the trampoline?
Trampoline mat is 1.25 m
above the ground

34. Calculate GPE
GPE relative to mat
Table of Variables
m = 45 kg
g = 10 m/s/s
h = 4 m
PE = mgh
PE = 45kg * -9.81
m/s/s * 4 m
PE = 1765.8 J
GPE relative to ground
Table of Variables
m = 45 kg
g = 10m/s/s
h = 5.25 m
PE = mgh
PE = 45kg * -9.81
m/s/s * 5.25 m
PE = 2317.6 J

35. Conversion of KE to GPE and
GPE to KE and KE to GPE and …

36. Strain Energy
When a fiberglass vaulting pole
bends, strain energy is stored in
the bent pole
Bungee jumping
When a tendon/ligament/muscle is
stretched, strain energy is stored
in the elongated elastin fibers
.

37. Work - Energy Relationship
The work done by an external force
acting on an object causes a change in
the mechanical energy of the object
  )
(
2
1 2
i
f
i
f r
r
mg
v
v
m
Fd
PE
KE
Fd
Energy
Fd









