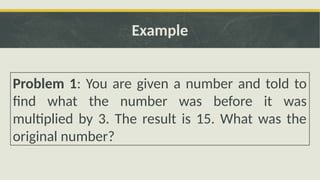
The document outlines the 'work backward' strategy, a problem-solving approach that begins with the desired outcome and reverses the steps to simplify the process. It details the steps involved in this strategy, provides examples of its application in solving mathematical problems and troubleshooting, and concludes by emphasizing the benefits of enhancing problem-solving skills through this method.

1. Work Backward Strategy
Presented by: Allysa Wong BSEd-Math III

2. What is the Work Backward Strategy?
Definition:
A problem-solving approach in which you start from the
desired outcome and reverse the steps to determine how
to reach that result.
This strategy can help simplify problems by thinking in
reverse order, often revealing paths or patterns that aren't
immediately obvious when thinking forward.

3. Steps in Work Backward Strategy
•Step 1: Identify the solution or final goal.
•Step 2: Work backward by figuring out what conditions
must have been true to reach the solution.
•Step 3: Eliminate possibilities that cannot logically lead to
the solution.
•Step 4: Simplify the problem by tracing the steps
backward and reducing complexity at each step.

4. Example
Problem 1: You are given a number and told to
find what the number was before it was
multiplied by 3. The result is 15. What was the
original number?

5. Solution
•Step 1: Start with the result (15).
•Step 2: Work backward by considering the operation
used (multiplication by 3).
•Step 3: Reverse the multiplication by dividing the result
(15) by 3.
•Step 4: 15÷3=5
•Conclusion: The original number is 5.

6. Example
Problem 2: You have a sequence of numbers (e.g., 2, 4,
8, 16, ?), and you need to figure out the next number in
the sequence.

7. Solution
•Step 1: Start with the last number (16)
•Step 2: Identify the pattern by working backward.
From 16 to 8,you can see that 16 ÷ 2 = 8.
From 8 to 4, you can see that 8 ÷ 2 = 4.
From 4 to 2, you can see that 4 ÷ 2 = 2.
•Step 3: Recognize the pattern.
•Step 4: Work forward to predict the next number. 16 × 2 = 32.
•Conclusion: Thus, the next number in the sequence is 32..

8. Real-World Application of Work
Backward
•Example 1: Solving Math Equations
In algebra, when you are given the solution, you can use
backward reasoning to find the values that lead to the
equation's result.
•Example 2: Troubleshooting
If you know the final outcome of a system (e.g., a machine
working correctly), you can reverse the steps to find the
cause of failure at earlier stages.

9. Conclusion
Understanding how and when to apply this
method enhances your problem-solving skills
and can lead to more efficient and effective
solutions.

10. Thank
You!

11. Add a Slide Title - 4

12. Add a Slide Title - 5
Click icon to add picture