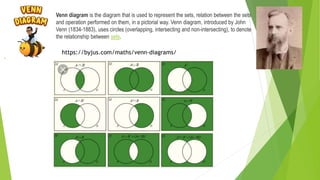
This document provides an introduction and overview of sets. It defines what a set is and introduces some key concepts related to sets, including subsets, universal sets, the empty set, cardinality, union, intersection, difference, equivalent sets, and Venn diagrams. It also provides examples to illustrate subsets, union, intersection, complement, and how to use Venn diagrams to represent sets and relationships between sets. Finally, it includes some practice problems involving sets to solve.

1. INTRODUCTION TO SETS
Content Standards:
The learner demonstrates understanding of key concepts of sets and
the real number system.
Performance Standards:
The learner is able to formulate challenging situations involving sets and
real numbers and solve these in a variety of strategies.

2. Most Essential Learning competencies
Week 1
The learner illustrates well-defined sets, subsets, universal sets, null
set, cardinality of sets, union and intersection of sets and the
difference of two sets.
Week 2
The learner solves problems involving sets with the use of Venn
Diagram.

3. HISTORY OF SETS

4. SETS- is a well-defined group of objects, called elements
that share a common characteristic.

5. H = {ladies hat, baseball cap, hard hat}
A = {a, b, c, d, e, f, g, h, i, j}
U = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9},
R = {x| x is a factor of 24}
S = { }

14. EQUIVALENT SETS- SETS HAVE THE
SAME NUMBER OF ELEMETS.

18. Cardinality of a set is a measure of the number of
elements in the set.
A= { a, b , c , d } A(n)= 4
B= { 1,2,3,4,5,6 } B(n) = 6
C= { } C(n) = 0
Empty set

19. Notations and Symbols

20. Subsets
A= { 1, 2 } S(A) = { (1,2), (1), (2), ()}
A(n) = 2 n² = 2² = 4
E= { m, a, t, h }
4² = 16

21. Union of Sets
1. A = { 1,2,3 } and B = { 1,2,4,5,6}
A U B = { 1,2,3,4,5,6}
2. M = { a, b, c } , N = { c, d, e, f } and P = { b, d, g }
M U N U P = { a, b, c, d, e, f, g }
Intersection of Sets
1. A = { 1,2,3} and B = { 1, 2, 4, 5, 6 }
A∩B = { 1, 2 }
2. C = { a, b, c, d }, D = { b, a, l , k } and E = { a, b, e, d, }
C∩D∩E = { a, b }

22. Complement of a Set
U = { 0,1,2,3,4,5,6,7,8,9 }
A= { 0,1,2,3 }
B= { 3,4,5,6,7}
C= {0,2,4,6,8 }
A’ = { 4,5,6,7,8,9 }
B’ = { 0,1,2,8,9 }
C’ = { 1,3,5,7,9 }
(A∩B)’
Find
Remember A∩B = { 3 }
Then, (A∩B)’ = { 0,1,2,4,5,6,7,8,9}

23. Venn diagram is the diagram that is used to represent the sets, relation between the sets
and operation performed on them, in a pictorial way. Venn diagram, introduced by John
Venn (1834-1883), uses circles (overlapping, intersecting and non-intersecting), to denote
the relationship between sets.
https://byjus.com/maths/venn-diagrams/

24. U = { 1,2,3,4,5,6,7,8} A { 1, 2, 3, 4} and B = { 3,4,5,6,7 }
Use Venn diagram to represent the elements
Use Venn diagram to represent the location of the sets
3, 4
1, 2 5,6,7
8

25. Use Venn diagram to represent the location of the elements
U = { a, b, c, d, e, f, g, h }
A = { a, b, c, d, e }, B = { c, d, e, f,} and C = { a, d, e , f, h}
d, e
c
b
f
a
h

26. 1. Let A and B be two finite sets such that n(A) = 20, n(B) = 28
and n(A ∪ B) = 36, find n(A ∩ B).
Solution:
Using the formula n(A ∪ B) = n(A) + n(B) - n(A ∩ B).
then n(A ∩ B) = n(A) + n(B) - n(A ∪ B)
= 20 + 28 - 36
= 48 - 36
= 12
Problems involving Sets

27. In a survey of university students, 64 had taken
mathematics course, 94 had taken chemistry course,
58 had taken physics course, 28 had taken
mathematics and physics, 26 had taken mathematics
and chemistry, 22 had taken chemistry and physics
course, and 14 had taken all the three courses. Find
how many had taken one course only
M(n) = 64
C(n) = 94
P(n)= 58
M∩P(n)=28
M∩C(n) = 26
C∩P(n) = 22
M ∩C ∩P (n) = 14
Solution:
14
8
12
14
24 60
22
Answers:
Mathematics = 24
Chemistry = 60
Physics = 22