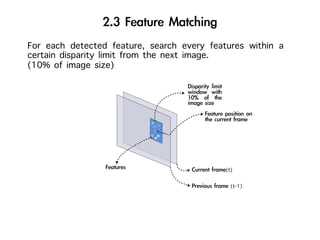
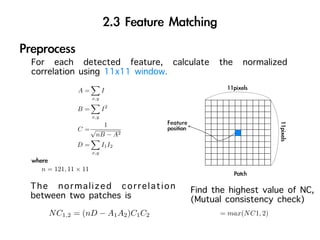
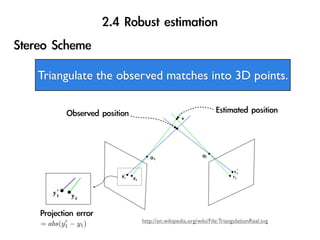
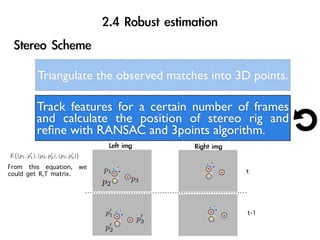
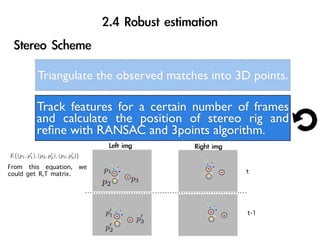
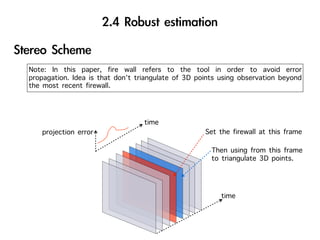
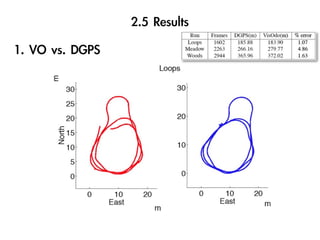
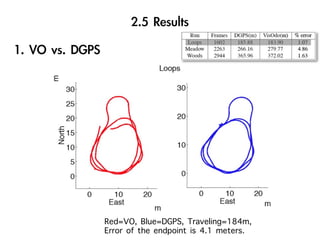
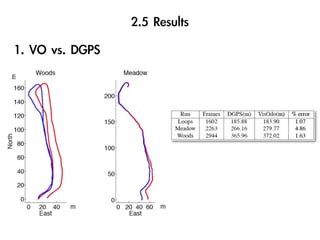
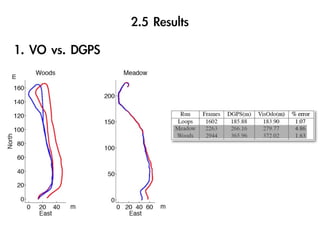
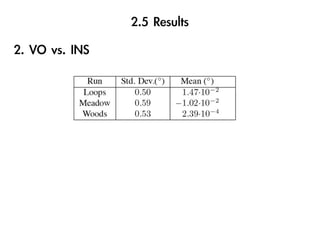
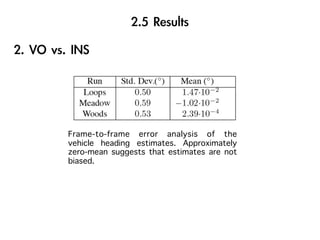
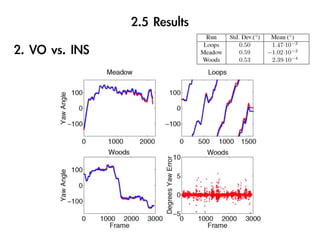
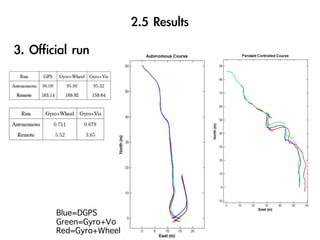
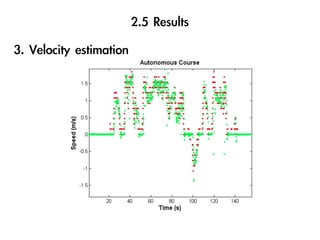
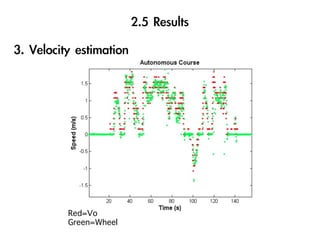
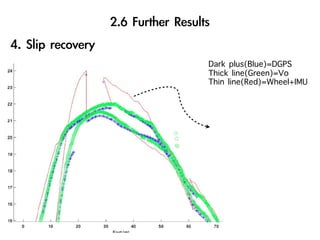
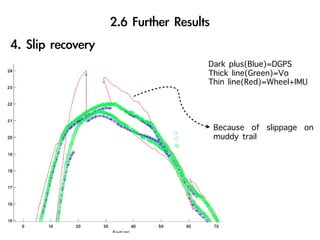
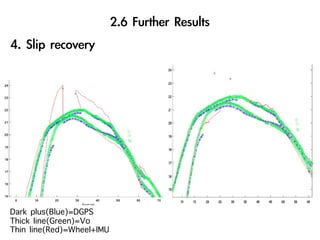
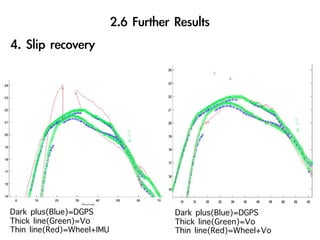
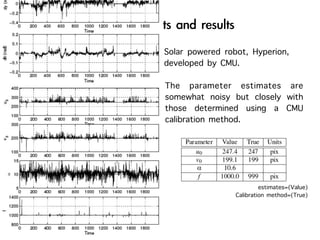
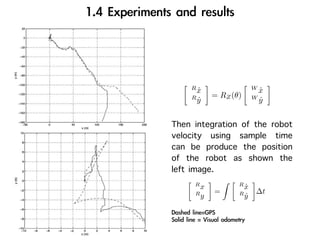
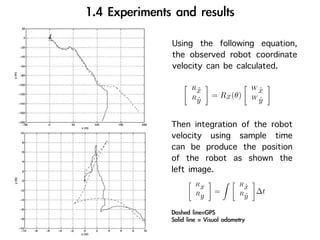
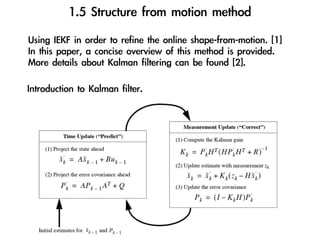
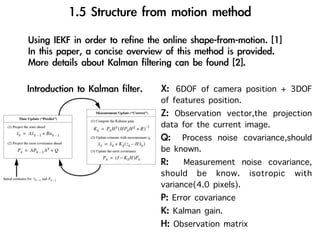
The document discusses visual odometry using laser and depth cameras, detailing their performance, accuracy, and applications. It highlights the Inect 3D depth camera's ability to capture 2D RGB and 3D depth images at 30Hz with reasonable pricing but notes its lower accuracy and high computational demands. It also covers techniques like RANSAC and triangulation for estimating positions and refining results in visual odometry.

1. Visual odometry
by Inkyu Sa

2. Motivation

3. Motivation
his laser scanner is good enough
to obtain the position (x, y, θ, z) of
the quadrotor at 10Hz. This data
provides from ROS canonical scan
matcher package.
0.5
0.4
0.3
0.2
0.1
y position(m)
0
−0.1
−0.2
−0.3
−0.4
−0.5
−0.5 −0.4 −0.3 −0.2 −0.1 0 0.1 0.2 0.3 0.4 0.5
x position(m)

4. Motivation
his laser scanner is good enough
to obtain the position (x, y, θ, z) of
the quadrotor at 10Hz. This data
provides from ROS canonical scan
matcher package.
0.5
0.4
0.3
0.2
- Relatively high accuracy. 0.1
y position(m)
- ROS device driver support. 0
−0.1
−0.2
−0.3
−0.4
−0.5
−0.5 −0.4 −0.3 −0.2 −0.1 0 0.1 0.2 0.3 0.4 0.5
x position(m)

5. Motivation
his laser scanner is good enough
to obtain the position (x, y, θ, z) of
the quadrotor at 10Hz. This data
provides from ROS canonical scan
matcher package.
0.5
0.4
0.3
0.2
- Relatively high accuracy. 0.1
y position(m)
- ROS device driver support. 0
−0.1
−0.2
- Expensive, USD 2375 −0.3
- Low frequency 10Hz −0.4
- Only for 2D. −0.5
−0.5 −0.4 −0.3 −0.2 −0.1 0 0.1 0.2 0.3 0.4 0.5
x position(m)

6. Motivation
http://www.ifixit.com

7. Motivation
inect 3D depth camera can
provide not only 2D RGB images but
3D depth images at 30Hz.
http://www.ifixit.com

8. Motivation
inect 3D depth camera can
provide not only 2D RGB images but
3D depth images at 30Hz.
http://www.ifixit.com
- Reasonable price. AUD 180.
- 3 Dimensional information.
- Openni Kinect ROS device driver and
point could library support.
- Available to use for visual odometry and
object recognition, 3D SLAM and so on.

9. Motivation
inect 3D depth camera can
provide not only 2D RGB images but
3D depth images at 30Hz.
http://www.ifixit.com
- Relatively low accuracy and many noise.
- Reasonable price. AUD 180.
- Heavy weight. original kinect over 500g.
- 3 Dimensional information.
- Openni Kinect ROS device driver and - Requires high computational power.
point could library support.
◦ ◦
- Narrow filed of view. H=57,V=43
- Available to use for visual odometry and
object recognition, 3D SLAM and so on.

10. Motivation
inect 3D depth camera can
provide not only 2D RGB images but
3D depth images at 30Hz.
http://www.ifixit.com
- Relatively low accuracy and many noise.
- Reasonable price. AUD 180.
- Heavy weight. original kinect over 500g.
- 3 Dimensional information.
- Openni Kinect ROS device driver and - Requires high computational power.
point could library support.
◦ ◦
- Narrow filed of view. H=57,V=43
- Available to use for visual odometry and
object recognition, 3D SLAM and so on.

11. Motivation
inect 3D depth camera can
provide not only 2D RGB images but
3D depth images at 30Hz.
http://www.ifixit.com
- Relatively low accuracy and many noise.
- Reasonable price. AUD 180.
- Heavy weight. original kinect over 500g.
- 3 Dimensional information.
- Openni Kinect ROS device driver and - Requires high computational power.
point could library support.
◦ ◦
- Narrow filed of view. H=57,V=43
- Available to use for visual odometry and
object recognition, 3D SLAM and so on.

12. Motivation
inect 3D depth camera can
provide not only 2D RGB images but
3D depth images at 30Hz.
http://www.ifixit.com
- Relatively low accuracy and many noise.
- Reasonable price. AUD 180.
- Heavy weight. original kinect over 500g.
- 3 Dimensional information.
- Openni Kinect ROS device driver and - Requires high computational power.
point could library support.
◦ ◦
- Narrow filed of view. H=57,V=43
- Available to use for visual odometry and
object recognition, 3D SLAM and so on.

13. Motivation
inect 3D depth camera can
provide not only 2D RGB images but
3D depth images at 30Hz.
http://www.ifixit.com
- Relatively low accuracy and many noise.
- Reasonable price. AUD 180.
- Heavy weight. original kinect over 500g.
- 3 Dimensional information.
- Openni Kinect ROS device driver and - Requires high computational power.
point could library support.
◦ ◦
- Narrow filed of view. H=57,V=43
- Available to use for visual odometry and
object recognition, 3D SLAM and so on.

14. Contents

15. Contents

18. ◦
◦ ◦

19. ◦
◦ ◦

20. ◦
◦ ◦

21.    
x a
 y =  b 
z 1
a = tan{α tan−1 u/f } cos β
b = tan{α tan−1 v/f } sin β
u =x point of image plane.
v =y point of image plane.

22. (∆x, ∆y, ∆θ)
(x , y )
(u, v) (u , v )
(x, y)
ˆ ˆ
(du, dv) = P (u, v, {u0 , v0 , f, α}, {∆x, ∆y, ∆θ})
P is optical flow function of
the feature coordinate.
t t+1

23. e1 = med ˆ ˆ
(dui − dui )2 ) + (dvi − dvi )2 )
e1

25. Solar powered robot, Hyperion,
developed by CMU.

26. Solar powered robot, Hyperion,
developed by CMU.
The parameter estimates are
somewhat noisy but closely with
those determined using a CMU
calibration method.
estimates=(Value)
Calibration method=(True)

27. R W
x
˙ x
˙
R = RZ (θ) W
y
˙ y
˙
Then integration of the robot
velocity using sample time
can be produce the position
of the robot as shown the
left image.
R R
x x
˙
R = R ∆t
y y
˙

28. Using the following equation,
the observed robot coordinate
velocity can be calculated.
R W
x
˙ x
˙
R = RZ (θ) W
y
˙ y
˙
Then integration of the robot
velocity using sample time
can be produce the position
of the robot as shown the
left image.
R R
x x
˙
R = R ∆t
y y
˙

31. 6DOF of camera position + 3DOF
of features position.
Observation vector,the projection
data for the current image.
Process noise covariance,should
be known.
Measurement noise covariance,
should be know. isotropic with
variance(4.0 pixels).
Error covariance
Kalman gain.
Observation matrix

32. − −
xk =
ˆ xk
ˆ + Kk (zk − H xk )
ˆ
The measurement is re-
projection of point.
T
zj = (R(ρ) Zj + t)
ρ, t are the camera-to-world rotation Euler angles and translation
of the camera.
Zj is the 3D world coordinate system position of point j.
This measurement is nonlinear in the estimated parameters and
this motivates use of the iterated extended Kalman filter.

33. − −
xk =
ˆ xk
ˆ + Kk (zk − H xk )
ˆ
The measurement is re-
projection of point.
T
zj = (R(ρ) Zj + t)
ρ, t are the camera-to-world rotation Euler angles and translation
of the camera.
Zj is the 3D world coordinate system position of point j.
This measurement is nonlinear in the estimated parameters and
this motivates use of the iterated extended Kalman filter.

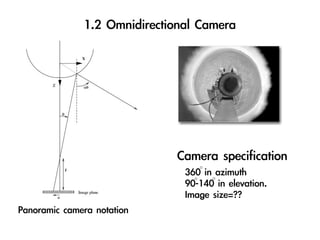
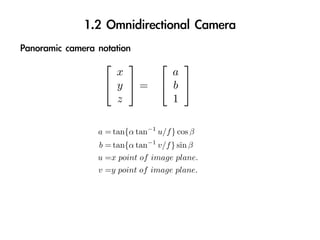
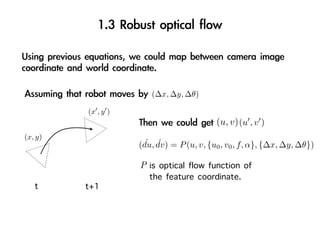
34. Initial state estimate distribution
is done using batch algorithm[1]
to get mean and covariance.
This estimates initial 6D camera
positions corresponding to
several images in the sequence.
29.2m traveled and average
error=22.9cm and maximum
error=72.7cm.

39. é

42. y
x

43. y Robert Collins CSE486, Penn State
x
λ1 = large , λ2 = small

44. y Robert Collins CSE486, Penn State
x
λ1 = small , λ2 = small

45. y Robert Collins CSE486, Penn State
x
λ1 = large , λ2 = large

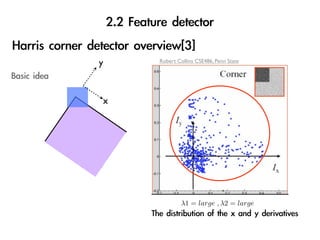
46. 2
E(u, v) = w(x, y)[I(x + u, y + v) − I(x, y)]
x,y
≈ [I(x, y) + uIx + vIy − I(x, y)]2
x,y
= u2 Ix + 2uvIx Iy + v 2 Iy
2 2
x,y
2
Ix Ix Iy u
= u v 2
Ix Iy Iy v
x,y
2
Ix Ix Iy u
= u v ( 2 )
Ix Iy Iy v
x,y
u 2
Ix Ix Iy
E(u, v) ∼
= u v M ,M = w(x, y) 2
v Ix Iy Iy
x,y

47. R = detM − k(traceM )2
2 2 2 2
= Ix Iy − k(Ix + Iy )
2
detM =λ1 λ2 α =Ix
2
traceM =λ1 + λ2 β =Iy
Ix =Gx ∗ I
k is an empirically determined σ
constant range from 0.04~0.06 Iy =Gy ∗ I
σ
2
Ix Ix Iy
M= w(x, y) 2
Ix Iy Iy
x,y

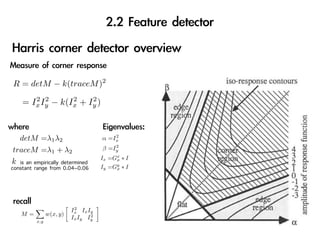
48. R = detM − k(traceM )2
2 2 2 2
= Ix Iy − k(Ix + Iy )
2
detM =λ1 λ2 α =Ix
2
traceM =λ1 + λ2 β =Iy
Ix =Gx ∗ I
k is an empirically determined σ
constant range from 0.04~0.06 Iy =Gy ∗ I
σ
2
Ix Ix Iy
M= w(x, y) 2
Ix Iy Iy
x,y
Source from [3]

50. For each detected feature, search every features within a
certain disparity limit from the next image.
(10% of image size)
(t)
(t-1)

51. For each detected feature, calculate the normalized
correlation using 11x11 window.
A= I
x,y
B= I2
x,y
1
C =√
nB − A2
D= I1 I2
x,y
n = 121, 11 × 11
The normalized correlation Find the highest value of NC,
between two patches is (Mutual consistency check)
N C1,2 = (nD − A1 A2 )C1 C2 = max(N C1, 2)

52. Circles shows the current feature locations
and lines are feature tracks over the images

53. Track matched features and estimate relative position
using 5-points algorithm. RANSAC refines position.

54. Track matched features and estimate relative position
using 5-points algorithm. RANSAC refines position.
Construct 3D points with first and last observation
and estimate the scale factor.

55. Track matched features and estimate relative position
using 5-points algorithm. RANSAC refines position.
Construct 3D points with first and last observation
and estimate the scale factor.
Track additional number of frames and compute the
position of camera with known 3D point using
3-point algorithm. RANSAC refines positions.

56. Track matched features and estimate relative position
using 5-points algorithm. RANSAC refines position.
Construct 3D points with first and last observation
and estimate the scale factor.
Track additional number of frames and compute the
position of camera with known 3D point using
3-point algorithm. RANSAC refines positions.

57. Triangulate the observed matches into 3D points.
http://en.wikipedia.org/wiki/File:TriangulationReal.svg
= abs(y1 − y1 )

58. Triangulate the observed matches into 3D points.
Track features for a certain number of frames
and calculate the position of stereo rig and
refine with RANSAC and 3points algorithm.
E{(p1 , p1 ), (p2 , p2 ), (p3 , p3 )}
From this equation, we p1
could get R,T matrix. t
p2 p3
p1 t-1
p3
p2

59. Triangulate the observed matches into 3D points.
Track features for a certain number of frames
and calculate the position of stereo rig and
refine with RANSAC and 3points algorithm.
E{(p1 , p1 ), (p2 , p2 ), (p3 , p3 )}
From this equation, we p1
could get R,T matrix. t
p2 p3
p1 t-1
p3
p2

60. Triangulate the observed matches into 3D points.
Track features for a certain number of frames
and calculate the position of stereo rig and
refine with RANSAC and 3points algorithm.
E{(p1 , p1 ), (p2 , p2 ), (p3 , p3 )}
From this equation, we p1
could get R,T matrix. t
p2 p3
p1 t-1
p3
p2

61. Triangulate the observed matches into 3D points.
Track features for a certain number of frames
and calculate the position of stereo rig and
refine with RANSAC and 3points algorithm.
Triangulate all new feature matches and repeat
previous step a certain number of time.

62. Triangulate the observed matches into 3D points.
Track features for a certain number of frames
and calculate the position of stereo rig and
refine with RANSAC and 3points algorithm.
Triangulate all new feature matches and repeat
previous step a certain number of time.

63. Note: In this paper, fire wall refers to the tool in order to avoid error
propagation. Idea is that don’t triangulate of 3D points using observation beyond
the most recent firewall.
time
projection error Set the firewall at this frame
Then using from this frame
to triangulate 3D points.
time

66. Image size: 720x240
Baseline: 28cm
HVOF: 50

67. Image size: 720x240
Baseline: 28cm
HVOF: 50

69. Visual Odometry’s frame processing rate
is around 13Hz.
No a priori knowledge of the motion.
3D trajectory is estimated.
DGPS accuray in RG-2 mode is 2cm

71. Red=VO, Blue=DGPS, Traveling=184m,
Error of the endpoint is 4.1 meters.

75. Frame-to-frame error analysis of the
vehicle heading estimates. Approximately
zero-mean suggests that estimates are not
biased.

78. Unit=metre
Autonomous run
GPS-(Gyro+Wheel)=0.29m
GPS-(Gyro+Vis)=0.77m
Remote control
GPS-(Gyro+Wheel)=-6.78m
Official runs to report results of visual GPS-(Gyro+Vis)=3.5m
odometry to DARPA. “Remote” means
manual control by a person who is not a
member of the vo team.
Distance from true DGPS position at the
end of eacho run. (in metres)

80. Blue=DGPS
Green=Gyro+Vo
Red=Gyro+Wheel

82. Red=Vo
Green=Wheel

83. Dark plus(Blue)=DGPS
Thick line(Green)=Vo
Thin line(Red)=Wheel+IMU

84. Dark plus(Blue)=DGPS
Thick line(Green)=Vo
Thin line(Red)=Wheel+IMU
Because of slippage on
muddy trail

85. Dark plus(Blue)=DGPS
Thick line(Green)=Vo
Thin line(Red)=Wheel+IMU

86. Dark plus(Blue)=DGPS Dark plus(Blue)=DGPS
Thick line(Green)=Vo Thick line(Green)=Vo
Thin line(Red)=Wheel+IMU Thin line(Red)=Wheel+Vo

94. Thank you