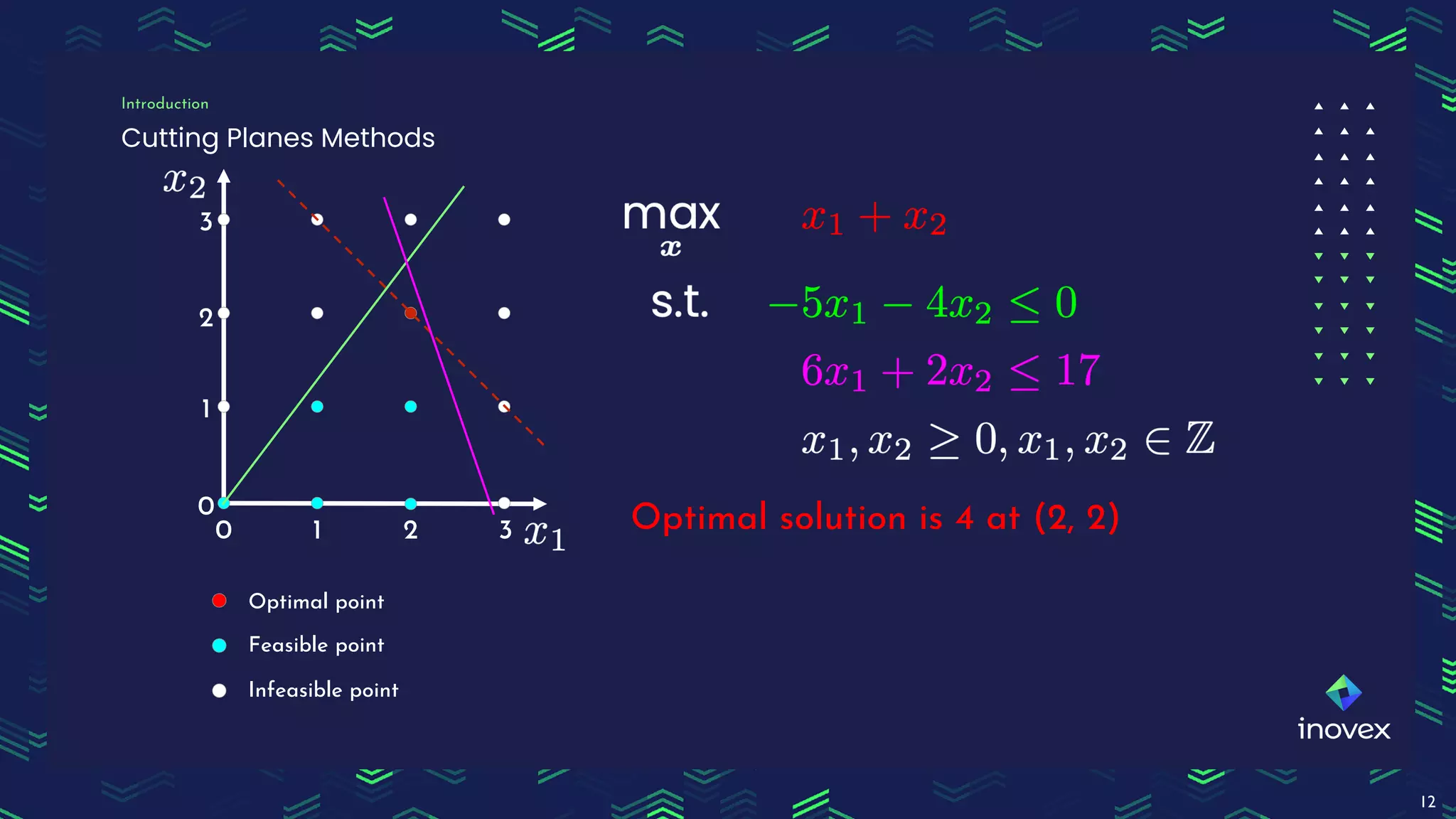
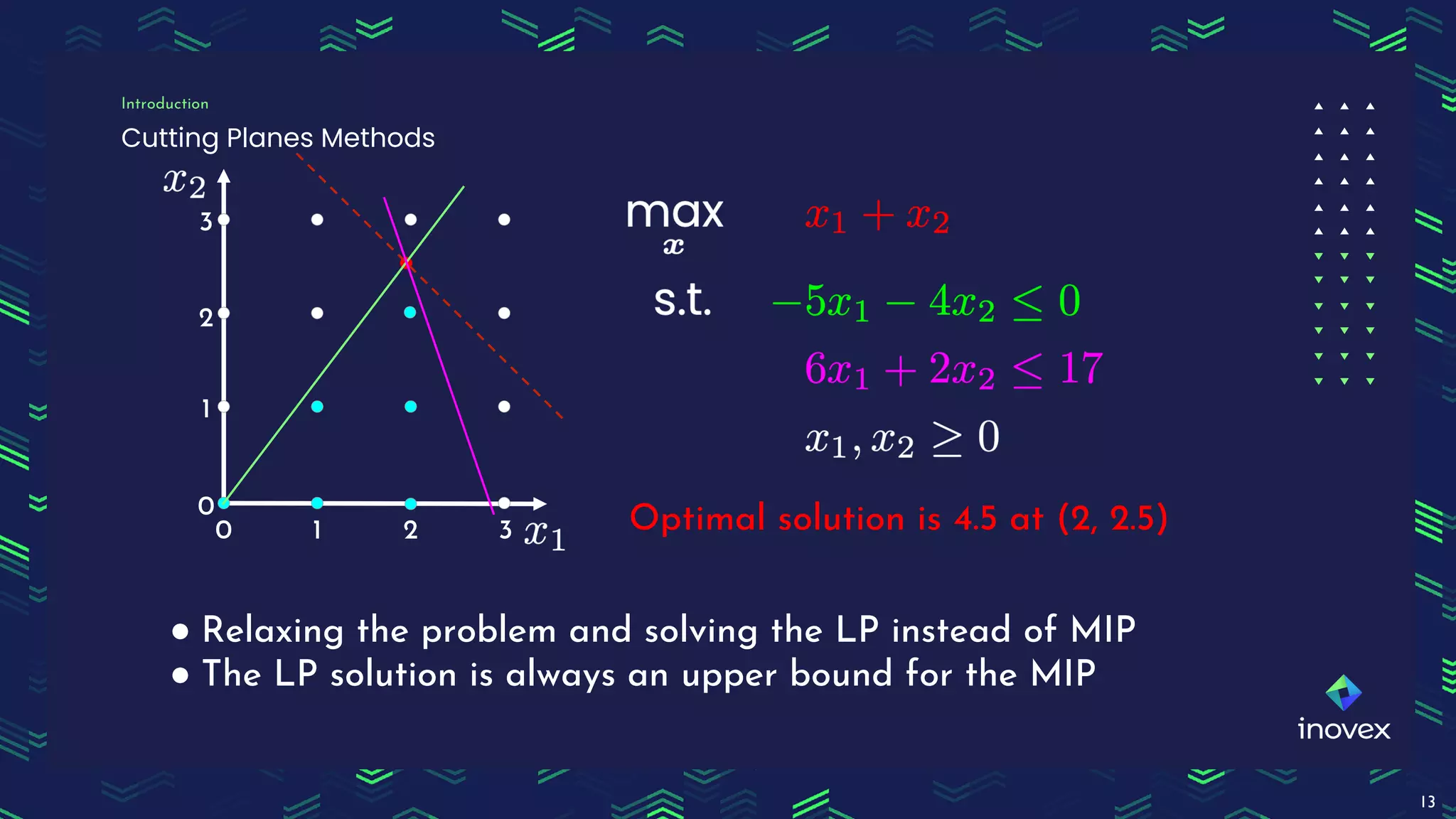
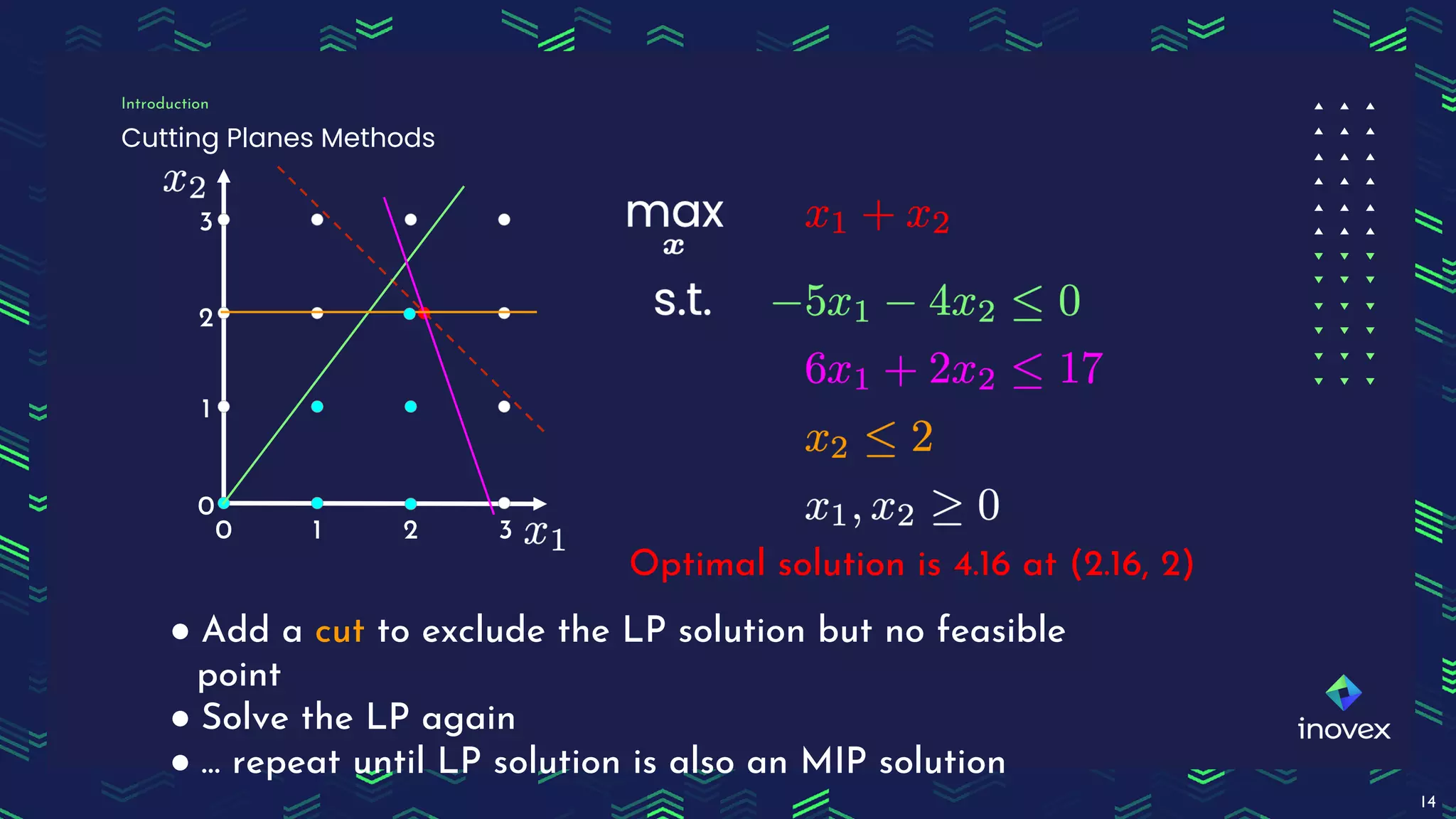
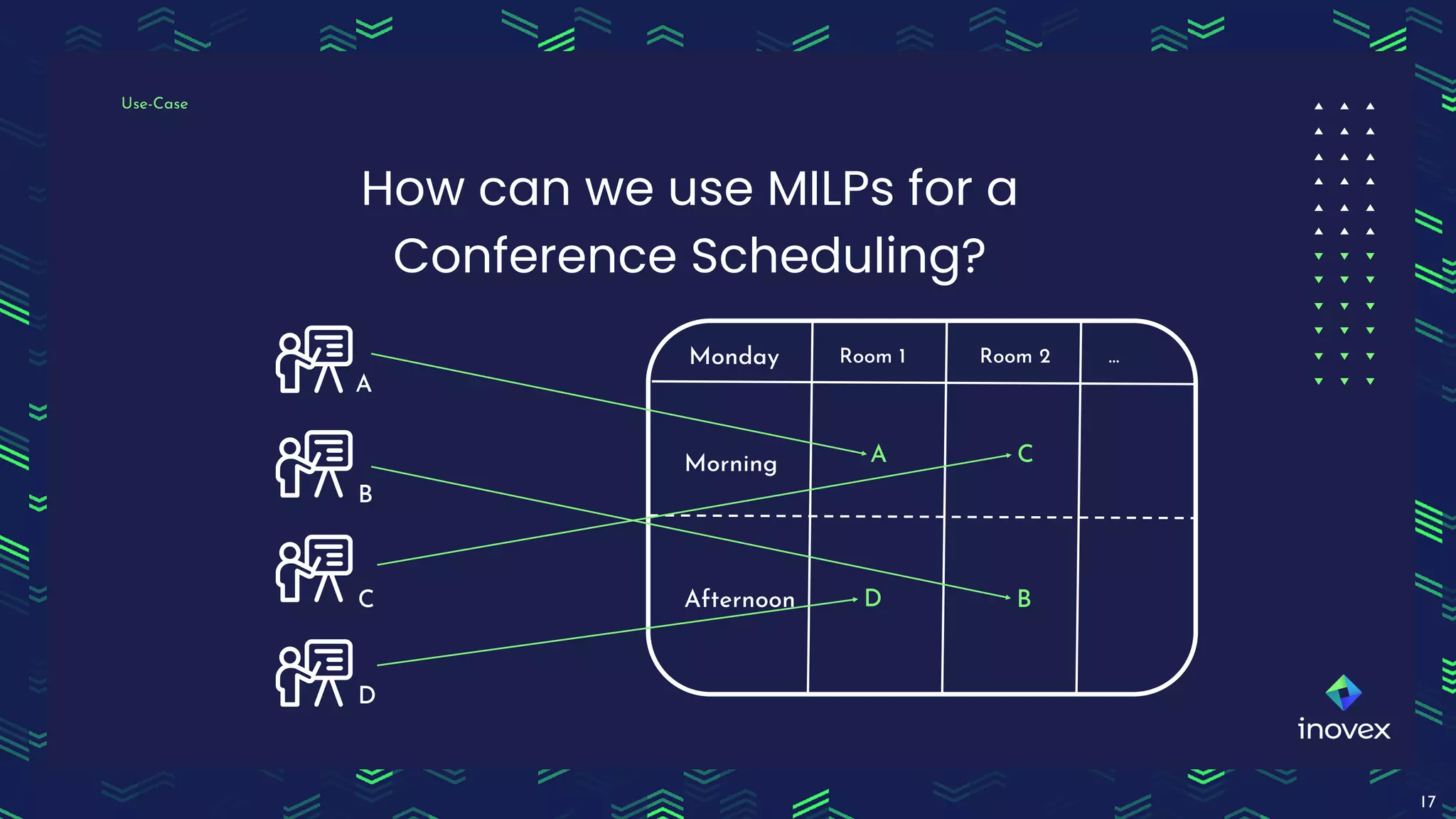
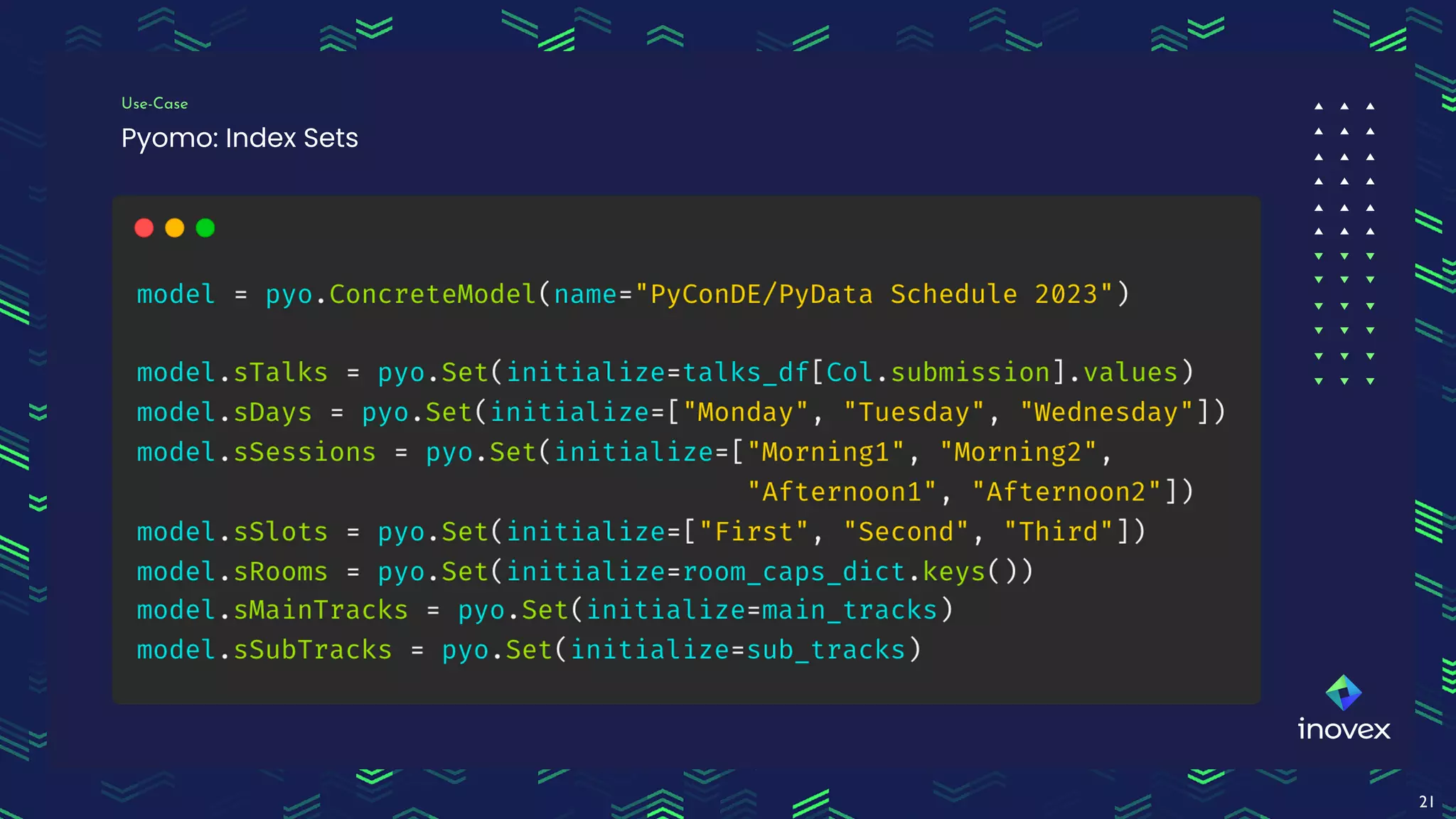
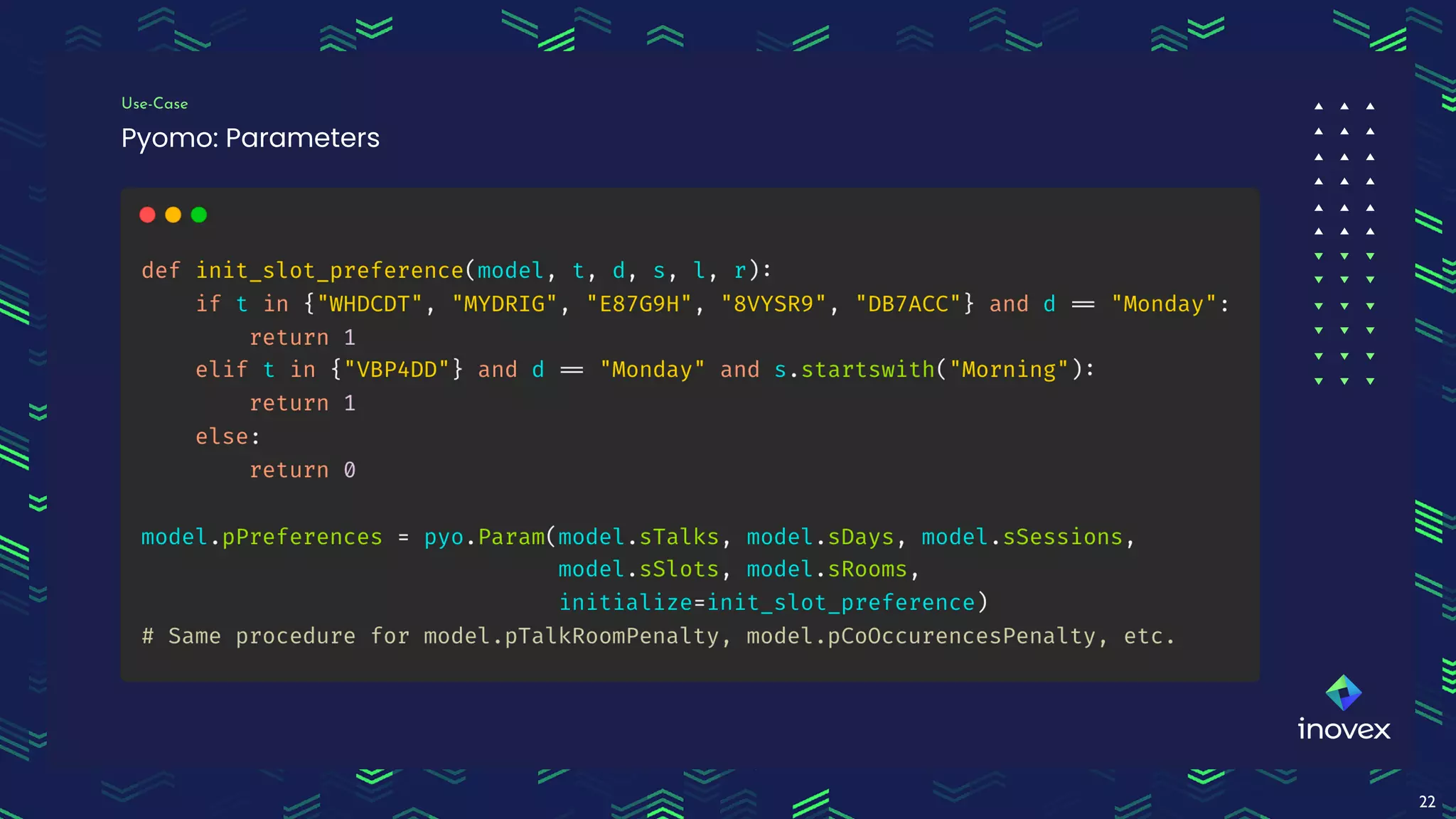
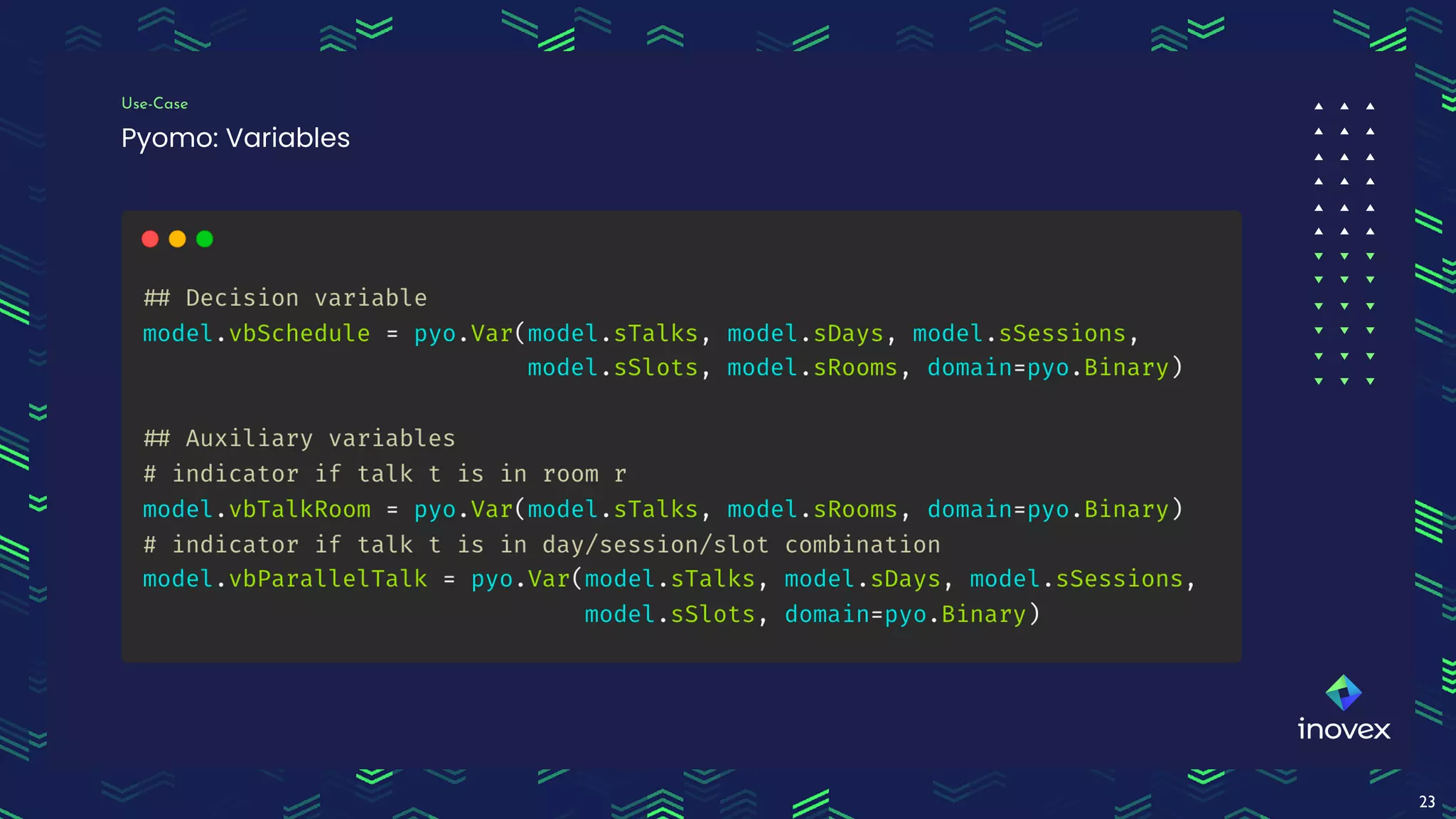
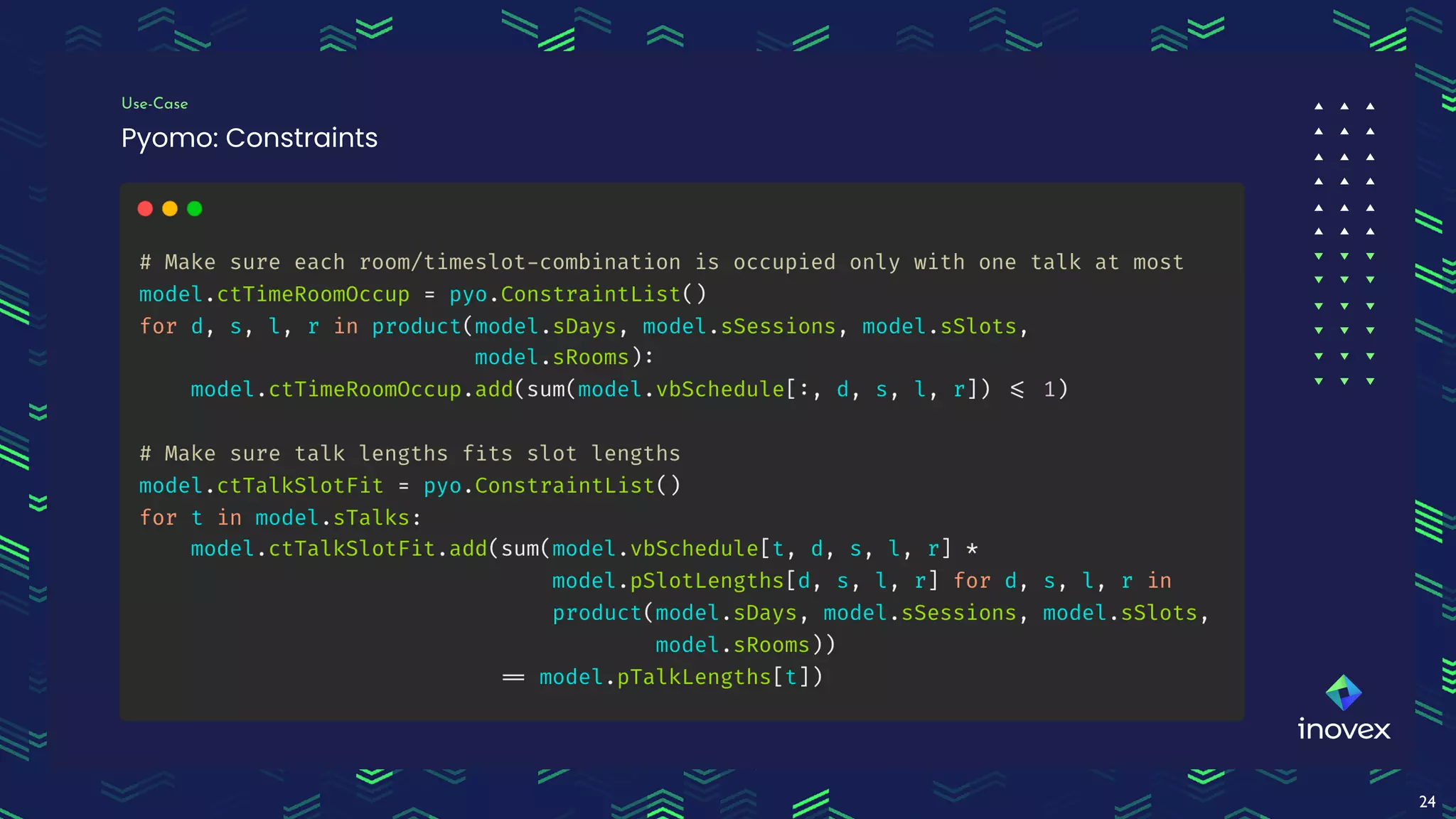
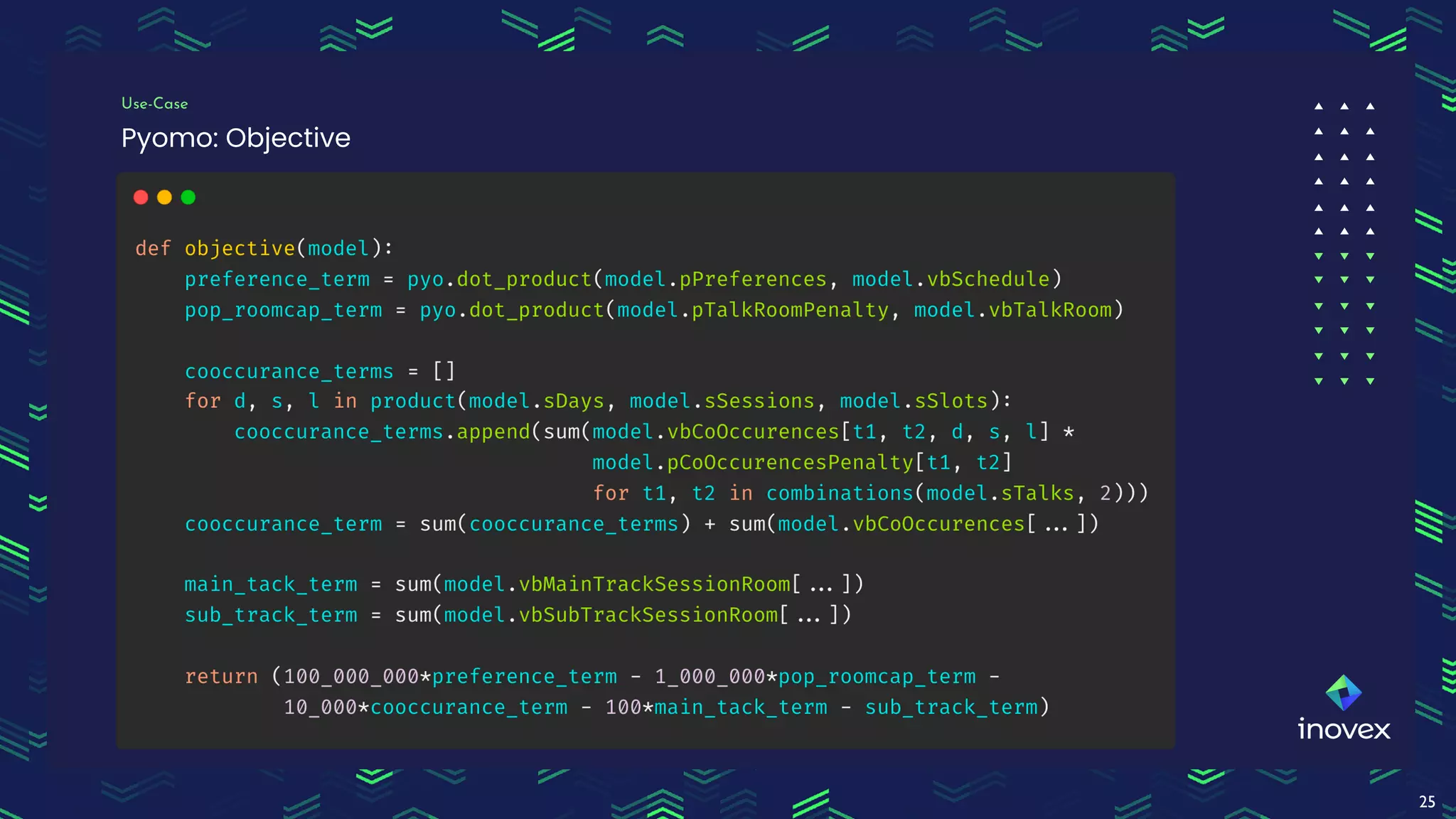
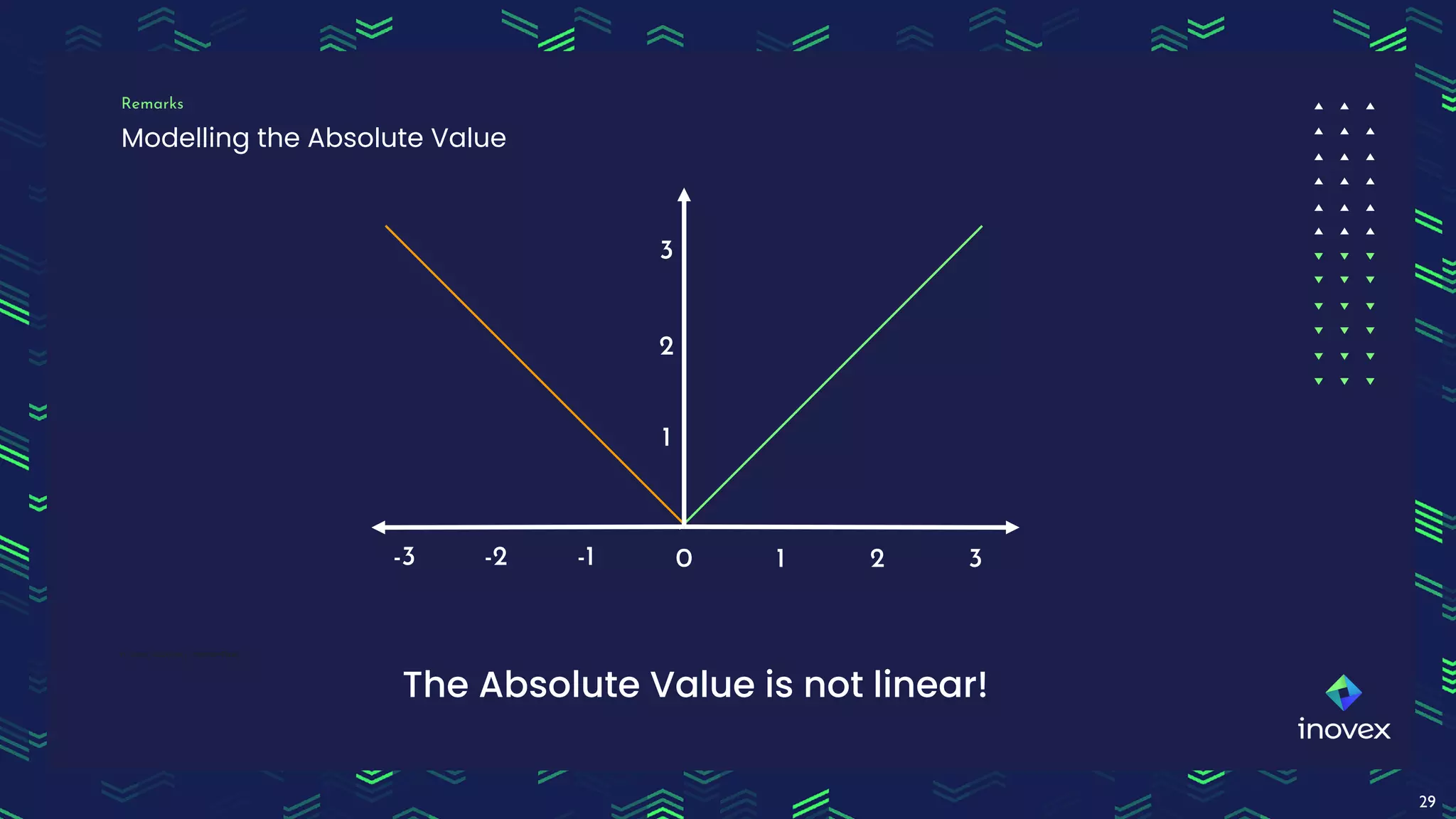
Dr. Florian Wilhelm discusses the application of integer programming in operations research, highlighting its importance in optimizing decision-making processes across various domains. The document covers common problem classes, definitions of linear and mixed integer programming, and methods for solving these problems, including cutting plane and branch & bound methods. Additionally, it emphasizes the practical use of mixed integer linear programming for scheduling events, showcasing the benefits of tools like Pyomo for modeling and solving optimization problems.

1. Florian Wilhelm
Unlocking the Power of
Integer Programming
Data Analytics & Science

2. Mathematical Modelling
Modern Data Warehousing & Analytics
Personalisation & RecSys
Uncertainty Quantification & Causality
Python Data Stack
OSS Contributor & Creator of PyScaffold
Dr. Florian Wilhelm
• HEAD OF DATA SCIENCE
FlorianWilhelm.info
florian.wilhelm@inovex.de
FlorianWilhelm
@FlorianWilhelm
2

3. ‣ Application Development (Web Platforms, Mobile
Apps, Smart Devices and Robotics, UI/UX design,
Backend Services)
‣ Data Management and Analytics (Business
Intelligence, Big Data, Searches, Data Science
and Deep Learning, Machine Perception and
Artificial Intelligence)
‣ Scalable IT-Infrastructures (IT Engineering, Cloud
Services, DevOps, Replatforming, Security)
‣ Training and Coaching (inovex Academy)
is an innovation and quality-driven
IT project house with a focus on
digital transformation.
Using technology to
inspire our clients.
And ourselves.
Berlin · Karlsruhe · Pforzheim · Stuttgart · München · Köln · Hamburg · Erlangen
www.inovex.de
3

4. Definition:
The objective of Operations Research (OR) is the
development and use of mathematical methods to support
decision-making processes in domains such as
manufacturing or finance.
Operations Research
Introduction
4

5. ● Assignment/Allocation Problem
How to schedule some talks in an agenda under some
constraints like room sizes to optimize the conference
experience?
● Transportation Problem
Which supplier should deliver to which factories given some
costs to satisfy each factory with minimal costs?
● Shortest Path Problem
Given some graph with a cost on each edge, what is the
shortest path from source to sink?
● Maximum Flow Problem
Given some pipe system with a source and sink, what is the
maximum flow through the system?
Common Problem Classes in Operations Research
Introduction
5

6. Definition of Linear Programming (LP)
Introduction
6
LPs can be solved with the Simplex algorithm in cubic on average
but exponential number of steps in worst case scenario or interior
point methods in about .

7. Definition of Mixed Integer Programming (MIP)
Introduction
7
MIPs are NP-hard, i.e. complexity grows exponentially with n
Dropping the integrality constraints, i.e. "linear relaxation", leads to
an LP problem.

8. If all variables need to be integer, it is a (pure)
integer linear program (ILP, IP).
If all variables need to be 0 or 1 (binary, boolean), it is a
0 - 1 linear program.
Special Cases of Mixed Integer Programming
Introduction
8

9. Given a set of items, each with a weight and a value,
determine which items to include in the collection so that the
total weight is less than or equal to a given limit and the
total value is as large as possible.
- Wikipedia
Knapsack problem
Introduction
9

10. 10
Solving a MILP
Introduction
Dropping the integrality constraints, i.e. “linear relaxation”, leads to an LP problem.
Two major method classes for solving MILPs:
● Cutting plane methods
● Branch and bound methods
Often combined as Branch and Cut methods
Source: Introduction to Optimization by Laurent Lessard, Spring 2017–18

11. Cutting Planes
Cutting Planes Methods
Introduction
11
Idea
● solve the LP relaxation problem
● while solution is not integral:
○ add constraint that excludes solution but no integer points
○ solve LP relaxation again

12. Cutting Planes Methods
Introduction
12
Optimal point
Feasible point
Infeasible point
0
1
2
3
1 2 3
0
Optimal solution is 4 at (2, 2)

13. Cutting Planes Methods
Introduction
13
0
1
2
3
1 2 3
0
Optimal solution is 4.5 at (2, 2.5)
● Relaxing the problem and solving the LP instead of MIP
● The LP solution is always an upper bound for the MIP

14. Cutting Planes Methods
Introduction
14
0
1
2
3
1 2 3
0
Optimal solution is 4.16 at (2.16, 2)
● Add a cut to exclude the LP solution but no feasible
point
● Solve the LP again
● … repeat until LP solution is also an MIP solution

15. Cutting Planes Methods
Introduction
15
0
1
2
3
1 2 3
0
Optimal solution is 4 at (2, 2)

16. Branch & Bound
Branch & Bound Methods
Introduction
16
Idea
1. solve the relaxed LP and for a fractional split into two
subproblems
○ with constraint
○ and with constraint
2. repeat step 1. and build a tree of subproblems
3. eliminate branches of the tree using

17. How can we use MILPs for a
Conference Scheduling?
Use-Case
17
Monday Room 1 Room 2 …
Morning
Afternoon
A
B
C
D
A
B
C
D

18. ● each talk must be assigned exactly once,
● each room/timeslot combination can only be occupied by
one talk at most,
● the length of the timeslot must match the length of the talk
● some tutorials have part 1 & 2, thus need to be consecutive
What Constraints do we have?
Use-Case
18

19. 1. the preferences for day and time of some speakers, e.g.
keynotes, need to be considered
2.popularity of a talk should be reflected in the room
capacity,
3.avoid parallel talks that attract the same audience,
4.have in the same session, i.e. consecutive block of talks, the
same main track, e.g. PyData vs. PyCon,
5.or even the same sub track, e.g. PyData: Data Handling,
What is our objective?
Use-Case
19
Precedence: 1 > 2 > 3 > 4 > 5

20. 1. Framework to formulate the problem, e.g.
a.Pyomo (OSS)
b.PuLP (OSS)
c.AMPL (Commercial)
d.…
2.Solver to solve the canonical problem, e.g.
a.HiGHS (OSS)
b.CBC (OSS)
c.Gurobi (Commercial)
d.IBM CPlex (Commercial)
e.…
Solving MILPs in Python
Use-Case
20

21. Pyomo: Index Sets
Use-Case
21

22. Pyomo: Parameters
Use-Case
22

23. Pyomo: Variables
Use-Case
23

24. Pyomo: Constraints
Use-Case
24

25. Pyomo: Objective
Use-Case
25

26. Solving the MILP Problem and Displaying model.vBScheduleSchedule
Use-Case
26

27. Pyomo / HiGHS notebook:
https://github.com/FlorianWilhelm/pytanis/blob/main/notebooks/pyconde-pydata-berlin-2023/50_scheduling_v1.ipynb
Check out the Full Source Code
Use-Case
27
Pytanis includes a Pretalx client and all
the tooling you need for conferences
using Pretalx, from handling the initial
call for papers to creating the final
program.

28. Looks easy enough! But is it really?
Remarks
28

29. m_caps_dict.keys(), ordered=True)
The Absolute Value is not linear!
Modelling the Absolute Value
Remarks
29
0
1
2
3
1 2 3
-1
-2
-3

30. m_caps_dict.keys(), ordered=True)
To model in the objective, we introduce auxiliary variables:
Modelling the Absolute Value
Remarks
30
1
2
3
1 2 3

31. 1. MILPs are an important tool in the domain of
Operations Research
2.Many optimal decision use-cases can be formulated
mathematically as a MILP, e.g. Knapsack problem
3.Solving a (M)ILP is NP-hard but good heuristics methods
exists like Branch & Cut
4.Tools like Pyomo translate your problem in a standardized
form and solver like HiGHS solve it
5.Modelling a problem as MILP, especially the Linearity
requirement, is the hardest part
Main Take-Aways
Summary
31

32. ● Introduction to Optimization by
Laurent Lessard
● Mixed Integer Programming for
time table scheduling by Francisco
Espiga
● Schedule Optimisation using Linear
Programming in Python by Lewis
Woolfson
● Some icons taken from
Flaticon.com
References
Summary
32

33. © 2023
Thank you!
Dr. Florian Wilhelm
Head of Data Science
EuroPython 2023
inovex.de
florian.wilhelm@inovex.de
@inovexlife
@inovexgmbh
waldstack.org
33