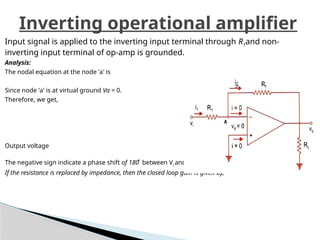
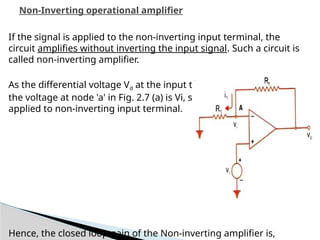
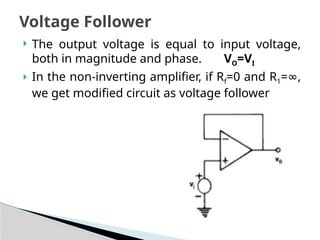
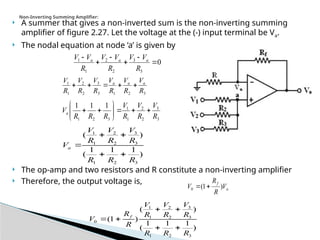
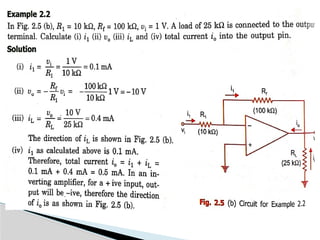
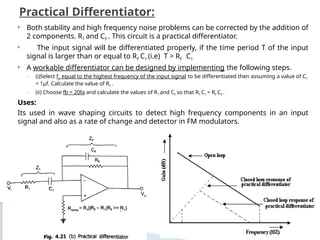
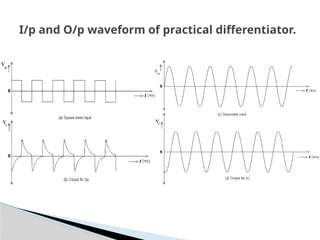
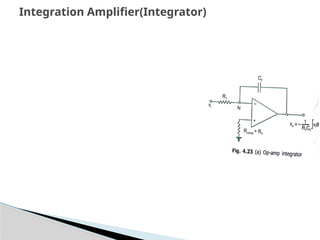
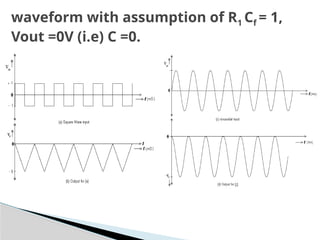
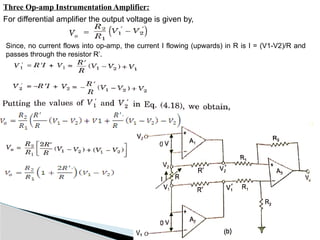
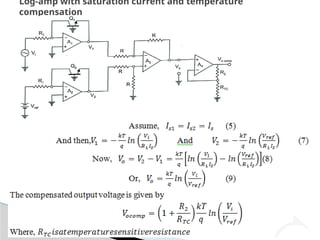
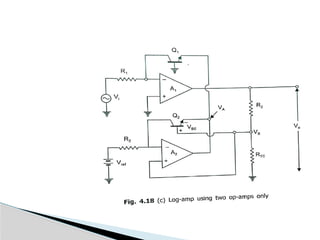
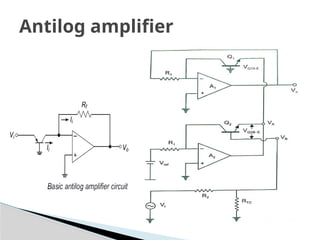
The document discusses various operational amplifier (op-amp) configurations and their applications, including inverting and non-inverting amplifiers, summing and differential amplifiers, as well as integrators and differentiators. It highlights the importance of closed-loop gain, common-mode rejection ratio (CMRR), and the unique functionalities of instrumentation amplifiers and log-antilog circuits. The applications outlined include temperature control, light intensity measurement, and analog weight scales, demonstrating the versatility of op-amps in electronic circuits.

1. Closed Loop Op Amp Configuration - Inverting
and Non-inverting Amplifiers- Inverter- Voltage
Follower Summing Amplifier, Averaging Circuits –
Subtractor -Differential Amplifier- Multiplier-
Differentiator- Integrator Instrumentation
amplifier, Precision rectifier-log and antilog
amplifiers- 1 st Order LPF, HPF and all pass
filters.
UNIT II
OPERATIONAL - AMPLIFIER APPLICATIONS

2. Input signal is applied to the inverting input terminal through R1and non-
inverting input terminal of op-amp is grounded.
Analysis:
The nodal equation at the node 'a' is
Since node 'a' is at virtual ground Va = 0.
Therefore, we get,
Output voltage
The negative sign indicate a phase shift of 180̊ between Vi and V0.
If the resistance is replaced by impedance, then the closed loop gain is given by,
Inverting operational amplifier

3. If the signal is applied to the non-inverting input terminal, the
circuit amplifies without inverting the input signal. Such a circuit is
called non-inverting amplifier.
As the differential voltage Vd at the input terminal of op-amp is zero,
the voltage at node 'a' in Fig. 2.7 (a) is Vi, same as the input voltage
applied to non-inverting input terminal.
Hence, the closed loop gain of the Non-inverting amplifier is,
Non-Inverting operational amplifier

4.  The output voltage is equal to input voltage,
both in magnitude and phase. VO=VI
 In the non-inverting amplifier, if Rf=0 and R1= ,
∞
we get modified circuit as voltage follower
Voltage Follower

5.  A typical summing amplifier with three input
voltages V1, V2 and V3 ,three input resistors R1,
R2, R3 and a feedback resistor Rf.
 The following analysis is carried out assuming
that the op-amp is an ideal one, that is, AOL = .
∞
Since the input bias current is assumed to be
zero, there is no voltage drop across the
resistor Rcomp and hence the non-inverting input
terminal is at ground potential.
Summing Amplifier:

6. )
2
(
3
)
(
,
3
,
)
1
(
)
(
)
(
,
,
)
(
)
(
0
,
0
,
0
3
2
1
0
3
2
1
3
2
1
0
3
2
1
0
3
2
1
3
3
2
2
1
1
0
3
3
2
2
1
1
0
0
3
3
2
2
1
1
0
3
3
2
2
1
1































































V
V
V
V
Then
R
R
R
R
If
V
V
V
V
R
R
V
V
V
V
Then
R
R
R
R
Sub
R
R
V
R
R
V
R
R
V
V
R
V
R
V
R
V
R
V
R
V
R
V
R
V
R
V
Then
V
Sub
R
V
V
R
V
V
R
V
V
R
V
V
f
f
f
f
f
f
f
f
f
a
f
a
a
a
a
The voltage at nod ‘a’ is zero as the non-inverting terminal is grounded. The
nodal equation be KCL at node ‘a’ is
Thus eqn (1) output Vo is the inverted sum of the input signals. Eqn (2) is output is the
average of the input signals (inverted).To find Rcomp, make all inputs V1 = V2 = V3 = 0. So
the effective input resistance Ri = R1 || R2 || R3.
Therefore, Rcomp = Ri || Rf = R1 || R2 || R3 || R,f.
Inverting Summing Amplifier:

7.  A summer that gives a non-inverted sum is the non-inverting summing
amplifier of figure 2.27. Let the voltage at the (-) input terminal be Va.
 The nodal equation at node ‘a’ is given by
 The op-amp and two resistors and R constitute a non-inverting amplifier
 Therefore, the output voltage is,
Non-Inverting Summing Amplifier:
0
3
3
2
2
1
1






R
V
V
R
V
V
R
V
V a
a
a
3
2
1
3
3
2
2
1
1
R
V
R
V
R
V
R
V
R
V
R
V a
a
a





3
3
2
2
1
1
3
2
1
1
1
1
R
V
R
V
R
V
R
R
R
Va 












)
1
1
1
(
)
(
3
2
1
3
3
2
2
1
1
R
R
R
R
V
R
V
R
V
Va





)
1
1
1
(
)
(
)
1
(
3
2
1
3
3
2
2
1
1
0
R
R
R
R
V
R
V
R
V
R
R
V f






a
f
V
R
R
V )
1
(
0 


9. 𝐴𝐶𝐿=
𝑉 0
𝑉 𝑖
=−
𝑅𝑓
𝑅1

11. A circuit that amplifies the difference between two signals is called
a difference or differential amplifier.
Since, the differential voltage at the input terminals of the op-amp
is zero, nodes 'a' and 'b' are at the name potential, designated as
v3.
The nodal equation at 'a' is.
and at 'b' is
Rearranging, we get
Subtract(1)-(2 ),
Differential amplifier

12. Difference-mode and Common-mode Gains:
The output voltage depends not only upon Vd, but is also affected by the average
voltage, called the common-mode signal Vcm defined as,
 (4)
even with the same voltage applied to both inputs, the output is not zero. The output,
therefore, must be ex­
pressed as,
where, A1 (A2)is the voltage amplification from input 1(2)
(6)
(4)+(6)
(4)-6)
Sub the value of v1 and v2 in eqn (5),we get
Where
And
ADM = voltage gain for the difference signal
and ACM = voltage gain for the common-mode signal

14. The relative sensitivity of an op-amp to a difference
signal as compared to a common-mode signal is called
common-mode rejection ratio (CMRR) and gives the
figure of merit p for the differential amplifier.
So,
CMRR is given by
CMRR is usually expressed in decibels (dB). Higher the
value of CMRR better is the op-amp.
Common-Mode Rejection Ratio

15. circuit performs the mathematical operation of differentiation
The differentiator may be constructed from a basic inverting
amplifier if an input resistor R1 is replaced by a capacitor C1.
The expression for the output voltage can be obtained KCL eqn
written at node V2 as follows,
At node VN is at virtual ground potential i.e.,VN=0, From eqn (1)
Differentiator
)
2
(
)
(
)
(
0
)
(
)
(
)
(
1
1
1
1


















dt
v
d
C
R
V
dt
v
d
C
R
V
R
V
dt
v
d
C
o
R
V
v
dt
v
v
d
C
in
F
o
in
F
o
F
o
in
F
N
o
N
in

16. Apply laplace transform,
=
Where,
 Disadvantages:
 At f=fa, i.e., 0 dB, and the gain increases at a rate
of 20dB/decade. This makes the circuit unstable
and break into oscillation.
 Sensitive to high frequency noise.
1
2
1
C
R
f
F
a



17.  Both stability and high frequency noise problems can be corrected by the addition of
2 components. R1 and CF . This circuit is a practical differentiator.
 The input signal will be differentiated properly, if the time period T of the input
signal is larger than or equal to RF C1 (i.e) T > RF C1
 A workable differentiator can be designed by implementing the following steps.
◦ (i)Select fa equal to the highest frequency of the input signal to be differentiated then assuming a value of C1
< 1μf. Calculate the value of RF .
◦ (ii) Choose fb = 20fa and calculate the values of R1 and CF so that R1 C1 = RF CF .
Uses:
Its used in wave shaping circuits to detect high frequency components in an input
signal and also as a rate of change and detector in FM modulators.
Practical Differentiator:

18. I/p and O/p waveform of practical differentiator.

19. Integration Amplifier(Integrator)

20. waveform with assumption of R1 Cf = 1,
Vout =0V (i.e) C =0.

21.  Practical Integrator to reduce the error voltage at the output,
a resistor RF is connected across the feedback capacitor CF .
 Both the stability and low frequency roll-off problems can be
corrected by the addition of a resistor RF in the practical
integrator.
 The gain limiting frequency fa is given by
Uses:
 Most commonly used in analog computers.
 ADC
 Signal wave shaping circuits
Practical Integrator (lossy integrator)
F
F
a
C
R
f

2
1


22.  The special amplifier which is used for such a low
level amplification with high CMRR, high input
impedance to avoid loading, low power
consumption and some other features is called as
instrumentation amplifier.
 The instrumentation amplifier is also called data
amplifier and is basically a difference amplifier.
 The expression for its voltage gain is generally of
the form,
 Where output of the amplifier,
 differential input which is to be
amplified
Instrumentation amplifier

23. For differential amplifier the output voltage is given by,
Since, no current flows into op-amp, the current I flowing (upwards) in R is I = (V1-V2)/R and
passes through the resistor R’.
Three Op-amp Instrumentation Amplifier:

24. Applications of instrumentation amplifier with practical circuits
(i)Temperature controller
(ii) Temperature Indicator:
The circuit shown above can be used as a Temperature Indicator.
As explained earlier, bridge is kept balanced at some reference temperature when Vo=0V.
The meter connected at the output is calibrated to reference temperature, corresponding to this reference
condition.
As temperature changes, amplifier output also changes. The meter can be calibrated to indicate the desired
temperature range by selecting the appropriate gain of the amplifier.
(iii). Light intensity meter:
The same circuit replacing thermistor with a photocell can be used as a simple Light intensity meter. The
bridge is kept balanced for the darkness condition.
When light falls on the photocell its resistance changes and produces unbalanced bridge condition. This
produces the output which in turn produces meter deflection.
The meter can be calibrated in terms of lux to measure the light intensity. Such a Light intensity meter is very
accurate and stable.
(iv). Analog weight scale:
The similar circuit but using strain gauges in all the four arms of the bridge can be used as a simple Analog
weight scale.
The elements are mounted on the base of the
weight platform.
When the weight is placed on the platform the
strain gauges in the opposite arm elongates while the
strain gauge in other two opposite arms get compressed.

25. The fundamental log-amp circuit is shown in above Fig., where a grounded base transistor
is placed in the feedback path. Since the collector is held at virtual ground and the base is
also grounded, the transistor's voltage-current relationship becomes that of a diode and is
given by,
(1)
Since, for a grounded base transistor,
(2)
k=Boltzmann’s constant, T=absolute temperature (in ˚K)
Therefore,
(3)
Or,
Taking natural log on both sides , we get
Also, from the above fig, 
So, (4)
Where
The output voltage is thus proportional to the logarithm of input voltage.
Scaling Log10 X=0.4343 ln X
Log and Antilog Amplifiers

26. Log-amp with saturation current and temperature
compensation

28. Antilog amplifier

31. Analog multiplier
 There are a number of applications of
analog multiplier such as
 frequency doubling,
 frequency shifting,
 phase angle detection.
 real power computation,
 multiplying two signals
 dividing and squaring of signals.

32.  A basic multiplier schematic symbol is shown in Fig. 4.20 (a). Two signal
inputs (vx and vy) are provided. The output is the product of the two
inputs divided by a reference voltage Vref.

33. the output of the multiplier will not saturate.
 If both inputs are positive. the IC is said to be a one quadrant
multiplier.
 A two quadrant multiplier will function properly if one input is held
positive and the other is allowed to swing both positive and negative.
 If both inputs may be either positive or negative, the IC is called a four
quadrant multiplier.

34. There can be several ways to make a circuit which will multiply according to Eq.
(4.55).
One commonly used technique is log-antilog method. The log-antilog method
relies on the mathematical relationship that the sum of the logarithm of two
numbers equals the logarithm of the product of those numbers.
 ln vx + ln vy = ln (vx vy) (4.56)
Figure 4.20 (b) is a block diagram of a log-antilog multiplier IC. Log -amps
require the input and reference voltages to be of the same polarity. This restricts
log-antilog multipliers to one quadrant opera­
tion.
Some of the multiplier IC chips avail­
able are AD533 and AD534.

35. Dividor:Division, the complement of multiplication, can be accomplished by
placing the multiolier ciucut element in the op amp’s feedback loop. The output
voltage from the divider with input signals vz and vx as dividend and divisor
respectively, is given by,
The result can be derived as follows. The op-amp’s inverting terminal is at virtual
ground. Therefore,