Download to read offline
Unidad 2
- 1. UNIDAD II PROGRAMACIÓN CUADRÁTICA Tienevariables cuadráticas o el producto de dos variables. La pendiente de una recta.- esta representa el grado de inclinación de una recta. 𝑚 = 𝑌2−𝑌1 𝑋2−𝑋1 𝑚 = tan ∝= 𝑦1 La distancia entre dos puntos.- 𝑑2 = (𝑥2− 𝑥1)2 + (𝑦2− 𝑦1)2 La distancia de un punto a la recta 𝑑 = | 𝑎𝑥 + 𝑏𝑦 + 𝑐 √𝑎2 + 𝑏2 EJEMPLOS 1) Minimizar la función:
- 2. UNIDAD II Minimizar lafunción Z= -1,197 No hay solución
- 3.
- 4. UNIDAD II EJERCICIO 1 𝑴𝒊𝒏𝒊𝒎𝒊𝒛𝒂𝒓𝒛 = ( 𝒙 𝟏 − 𝟐) 𝟐 + ( 𝒙 𝟐 − 𝟐) 𝟐 s.a 𝑥1 + 2𝑥2 ≤ 3 8𝑥1 + 5𝑥2 ≥ 10 𝑥 𝑖 ≥ 0 𝑪 = (𝟐; 𝟐) 𝒙 𝟏 + 𝟐𝒙 𝟐 = 𝟑 X1 X2 0 3/2 3 0 (3;1.5) 0≤3 Verdadero 𝟖𝒙 𝟏 + 𝟓𝒙 𝟐 = 𝟏𝟎 X1 X2 0 2 5/4 0 (1.25;2) 0≥10 𝑥1 + 2𝑥2 = 3 𝑥2 = −𝑥1 + 3 2 𝑥2 = − 1 2 𝑥1 + 3 2 𝑚1 = − 1 2 𝒎 𝟏 ∗ 𝒎 𝟐 = −𝟏 − 1 2 ∗ 𝑚2 = −1 𝑚2 = 2 𝒚 − 𝒚 𝟏 = 𝒎(𝒙 − 𝒙 𝟏) 𝑦 − 2 = 2(𝑥 − 2) 𝑥2 − 2 = 2( 𝑥1 − 2) 𝑥2 − 2 = 2𝑥1 − 4 −2𝑥1 + 𝑥2 = −2 2𝑥1 − 𝑥2 = 2
- 5. UNIDAD II 2𝑥1 −𝑥2 = 2 (-2) 𝑥1 + 2𝑥2 = 3 2𝑥1 − 𝑥2 = 2 −2𝑥1 − 4𝑥2 = −6 −5𝑥2 = −4 𝒙 𝟐 = 𝟒/𝟓 2𝑥1 − 4 5 = 2 𝑥1 = 2 + 4 5 2 𝒙 𝟏 = 𝟕 𝟓 𝑑 = | 𝑎𝑥+𝑏𝑦+𝑐 √𝑎2+𝑏2 𝑑 = | 2(2)+(−1)(2)+2 √22 +22 𝑑 = | 4 √8 𝑑 = |1.41 𝑅𝑒𝑒𝑚𝑝𝑙𝑎𝑧𝑎𝑟 𝑒𝑛 𝑍 𝑧 = ( 7 5 − 2) 2 + ( 4 5 − 2) 2 𝑧 = 1.8 𝑴𝒊𝒏𝒊𝒎𝒊𝒛𝒂𝒓 𝒁 = −𝟔𝒙 𝟏 − 𝟏𝟑𝒙 𝟐 − 𝒙 𝟏 𝒙 𝟐 − 𝟒𝒙 𝟏 𝟐 − 𝟒𝒙 𝟐 𝟐 s.a 𝑥2 + 𝑥3 = 20 𝑥1 + 𝑥2 + 𝑥4 = 23 𝑥1 ≥ 0 𝑅𝑒𝑠𝑜𝑙𝑢𝑐𝑖ó𝑛: 𝒙 𝟑 = 0 𝒙 𝟒 = 0 𝒙 𝟐 = 20 𝒙 𝟏 + 𝒙 𝟐 + 𝒙 𝟒 = 𝟐𝟑 𝒙 𝟏 + 20 + 0 = 23 𝒙 𝟏 = 3
- 6. UNIDAD II 𝑍 =−6(3)− 13(20)− 3(20) − 4(3)2 − 4(202) 𝑍 = 1974 𝑴𝒊𝒏𝒊𝒎𝒊𝒛𝒂𝒓 𝒁 = ( 𝒙 𝟏 − 𝟔) 𝟐 + ( 𝒙 𝟐 − 𝟖) 𝟐 S.a. 𝑥1 ≤ 7 𝑥2 ≤ 5 𝑥1 + 2𝑥2 ≤ 12 𝑥1 + 𝑥2 ≤ 9 𝑥 𝑖 ≥ 0 𝒙 𝟏 = 7 𝒙 𝟐 = 5 𝒙 𝟏 + 𝟐𝒙 𝟐 = 𝟏𝟐 X1 X2 0 6 12 0 (12; 6) 0≤12 Verdadero 𝒙 𝟏 + 𝒙 𝟐 = 𝟗 X1 X2 0 9 9 0 (9;9) 0≤9 Verdadero
- 7. UNIDAD II 𝑑 =| 𝑎𝑥+𝑏𝑦+𝑐 √𝑎2+𝑏2 𝑑 = | 1(6)++2(8)(2)−12 √12 +22 𝑑 = | 10 √5 𝑑 = |4.47 (𝑋1 − ℎ)2 + ( 𝑋2 − 𝑘)2 = 𝑅 (𝑋1 − 6)2 + ( 𝑋2 − 8)2 = ( 10 √5 ) 2 Despejo 𝑋1 de 𝑥1 + 2𝑥2 = 12 𝑥1 = −2𝑥2 + 12 .- Reemplazo en la ecuación de la circunferencia: (−2𝑥2 + 12 − 6)2 + ( 𝑋2 − 8)2 = 20 (6 − 2𝑥2)2 + ( 𝑋2 − 8)2 = 20 36 − 4𝑥2 + 4𝑥2 + 𝑥2 − 16𝑥2 + 64 − 20 = 0 5𝑥2 2 − 20𝑥2 + 80 = 0 5𝑥2 2 − 20𝑥2 + 80 = 0 5 𝑥2 2 − 4𝑥2 + 16 = 0 (𝑥2 − 4)^2 = 0 𝑥2 = 4 𝑥1 = 12 − 8 𝑥1 = 4 𝑬𝑱𝑬𝑹𝑪𝑰𝑪𝑰𝑶 𝟓 𝑀𝐴𝑋𝐼𝑀𝐼𝑍𝐴𝑅 𝑍 = ( 𝑋 − 3)2 + ( 𝑌 − 1)2 S.a. 2𝑋 + 𝑌 ≤ 2 𝑋 + 3𝑌 ≤ 3 𝑌 ≤ 4 C= (3,1) 2𝑋 + 𝑌 ≤ 2 X Y
- 8. UNIDAD II 0 2 10 (1,2) 𝑉𝑒𝑟𝑑𝑎𝑑𝑒𝑟𝑜 𝑋 + 3𝑌 ≤ 3 X Y 0 1 3 0 (3,1) 𝑉𝑒𝑟𝑑𝑎𝑑𝑒𝑟𝑜 Y=4 𝑉𝑒𝑟𝑑𝑎𝑑𝑒𝑟𝑜 𝑑 = | 𝑎𝑥+𝑏𝑦+𝑐 √𝑎2+𝑏2 𝑑 = | 2(3)+1(1)−2 √4+1 𝑑 = | 5 √5 𝑑 = |2.24 ( 𝑋 − 3)2 + ( 𝑌 − 1)2 = ( 5 √5 ) 2 2𝑋 + 𝑌 = 2 𝑌 = 2 − 2𝑋 ( 𝑋 − 3)2 + (2 − 2𝑋 − 1)2 = 5 𝑋2 − 6𝑋 + 9 + (1 − 2𝑋)2 = 5 𝑋2 − 6𝑋 + 9 + 1 − 4𝑋 + 4𝑋2 − 5 = 0 5𝑋2 − 10𝑋 + 5 = 0 5 𝑋2 − 2𝑋 + 1 = 0 ( 𝑋 − 1)^2 =0 𝑿 = 𝟏 𝑌 = 2 − 2(1) 𝒀 = 𝟎
- 9. UNIDAD II 𝑴𝑰𝑵𝑰𝑴𝑰𝒁𝑨𝑹 𝒇(𝒙) = 𝒙 𝟐 + 𝟐𝒙 − 𝟑 𝑅𝑒𝑝𝑟𝑒𝑠𝑒𝑛𝑡𝑎 𝑙𝑎 𝑒𝑐𝑢𝑎𝑐𝑖ó𝑛 𝑑𝑒 𝑢𝑛𝑎 𝑝𝑎𝑟á𝑏𝑜𝑙𝑎 𝑃𝑎𝑟𝑎 ℎ𝑎𝑙𝑙𝑎𝑟 𝑒𝑙 𝑣é𝑟𝑡𝑖𝑐𝑒 𝑒𝑛 𝑋 𝑉𝑋 = −𝑏 2𝑎 𝑉𝑋 = −2 2(1) 𝑉𝑋 = −1 𝑃𝑎𝑟𝑎 ℎ𝑎𝑙𝑙𝑎𝑟 𝑒𝑙 𝑣é𝑟𝑡𝑖𝑐𝑒 𝑒𝑛 𝑌 𝑉𝑌 = (−1)2 + (2)(−1)− 3 𝑉𝑌 = −4 𝑉é𝑟𝑡𝑖𝑐𝑒 𝑑𝑒 𝑙𝑎 𝑝𝑎𝑟á𝑏𝑜𝑙𝑎 (-1,-4) 𝑃𝑢𝑛𝑡𝑜𝑠 𝑑𝑒 𝑐𝑜𝑟𝑡𝑒 𝑝𝑎𝑟𝑎f(x) o y; x=0 𝑓( 𝑥) = 𝑥2 + 2𝑥 − 3 𝑓( 𝑥) = 02 + 2(0) − 3 𝑓( 𝑥) = −3 𝑃𝑢𝑛𝑡𝑜 𝑑𝑒 𝑐𝑜𝑟𝑡𝑒 (0,-3) Punto de corte para x; f(x)=0 𝑜 = 𝑥2 + 2𝑥 − 3 𝑥2 + 2𝑥 − 3 = 0 ( 𝑥 + 3)( 𝑥 − 1) = 0 𝑥1 = −3 𝑥2 = 1
- 10. UNIDAD II ALGORITMO DERAMIFICACIÓN Y ACOTAMIENTO 𝑥 ≤ ⟦ 𝑎⟧ 𝑥 ≥ ⟦ 𝑎⟧ + 1 ⟦−3,5⟧ = −4 ⟦−3,8⟧ = −4 ⟦−3,2⟧ = −4 ⟦2,5⟧ = 2 ⟦2,8⟧ = 2 ⟦2,1⟧ = 2 𝐸𝑛 𝑒𝑠𝑡𝑎 𝑡é𝑐𝑛𝑖𝑐𝑎 𝑎𝑙 𝑚𝑎𝑥𝑖𝑚𝑖𝑧𝑎𝑟 𝑒𝑛𝑐𝑜𝑛𝑡𝑟𝑎𝑚𝑜𝑠 𝑒𝑙 𝑚𝑒𝑛𝑜𝑟 𝑣𝑎𝑙𝑜𝑟, 𝑦 𝐴𝑙 𝑚𝑖𝑛𝑖𝑚𝑖𝑧𝑎𝑟 𝑒𝑛𝑐𝑜𝑛𝑡𝑟𝑎𝑚𝑜𝑠 𝑒𝑙 𝑚𝑎𝑦𝑜𝑟 𝑣𝑎𝑙𝑜𝑟. 𝑨𝑳𝑮𝑶𝑹𝑰𝑻𝑴𝑶 𝑫𝑬 𝑩𝑹𝑨𝑵𝑪𝑯 𝑨𝑵𝑫 𝑩𝑶𝑼𝑵𝑫 (𝑹𝑨𝑴𝑰𝑭𝑰𝑪𝑨𝑪𝑰Ó𝑵 𝒀 𝑨𝑪𝑶𝑻𝑨𝑴𝑰𝑬𝑵𝑻𝑶) 𝐸𝑠 𝑢𝑛 𝑎𝑙𝑔𝑜𝑟𝑖𝑡𝑚𝑜 𝑑𝑖𝑠𝑒ñ𝑎𝑑𝑜 𝑝𝑎𝑟𝑎 𝑙𝑎 𝑟𝑒𝑠𝑜𝑙𝑢𝑐𝑖ó𝑛 𝑑𝑒 𝑚𝑜𝑑𝑒𝑙𝑜𝑠 𝑑𝑒 𝑝𝑟𝑜𝑔𝑟𝑎𝑚𝑎𝑐𝑖ó𝑛 𝑒𝑛𝑡𝑒𝑟𝑎, 𝑠𝑖𝑛 𝑒𝑚𝑏𝑎𝑟𝑔𝑜, 𝑒𝑠 𝑚𝑢𝑦 𝑓𝑟𝑒𝑐𝑢𝑒𝑛𝑡𝑒 𝑞𝑢𝑒 𝑙𝑎 𝑛𝑎𝑡𝑢𝑟𝑎𝑙𝑒𝑧𝑎 𝑑𝑒𝑙 𝑝𝑟𝑜𝑏𝑙𝑒𝑚𝑎 𝑛𝑜𝑠 𝑖𝑛𝑑𝑖𝑞𝑢𝑒 𝑞𝑢𝑒 𝑙𝑎𝑠 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠 𝑠𝑜𝑛 𝑒𝑛𝑡𝑒𝑟𝑎𝑠 𝑜 𝑏𝑖𝑛𝑎𝑟𝑖𝑎𝑠. 𝑆𝑢 𝑜𝑝𝑒𝑟𝑎𝑡𝑜𝑟𝑖𝑎 𝑐𝑜𝑛𝑠𝑖𝑠𝑡𝑒 𝑒𝑛 𝑟𝑒𝑠𝑜𝑙𝑣𝑒𝑟 𝑒𝑠𝑡𝑒 𝑐𝑜𝑚𝑜 𝑠𝑖 𝑓𝑢𝑒𝑠𝑒 𝑢𝑛 𝑚𝑜𝑑𝑒𝑙𝑜 𝑑𝑒 𝑝𝑟𝑜𝑔𝑟𝑎𝑚𝑎𝑐𝑖ó𝑛 𝑙𝑖𝑛𝑒𝑎𝑙 𝑦 𝑙𝑢𝑒𝑔𝑜 𝑔𝑒𝑛𝑒𝑟𝑎𝑟 𝑐𝑜𝑡𝑎𝑠 𝑒𝑛 𝑐𝑎𝑠𝑜 𝑞𝑢𝑒 𝑎𝑙 𝑚𝑒𝑛𝑜𝑠 𝑢𝑛𝑎 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒 𝑑𝑒 𝑑𝑒𝑐𝑖𝑠𝑖ó𝑛 𝑎𝑑𝑜𝑝𝑡𝑒 𝑢𝑛 𝑣𝑎𝑙𝑜𝑟 𝑓𝑟𝑎𝑐𝑐𝑖𝑜𝑛𝑎𝑟𝑖𝑜 𝐸𝑙 𝑎𝑙𝑔𝑜𝑟𝑖𝑡𝑚𝑜 𝑔𝑒𝑛𝑒𝑟𝑎 𝑒𝑛 𝑓𝑜𝑟𝑚𝑎 𝑟𝑒𝑐𝑢𝑟𝑠𝑖𝑣𝑎 𝑐𝑜𝑡𝑎𝑠 ( 𝑜 𝑟𝑒𝑠𝑡𝑟𝑖𝑐𝑐𝑖𝑜𝑛𝑒𝑠 𝑎𝑑𝑖𝑐𝑖𝑜𝑛𝑎𝑙𝑒𝑠) 𝑞𝑢𝑒 𝑓𝑎𝑣𝑜𝑟𝑒𝑐𝑒𝑛 𝑙𝑎 𝑜𝑏𝑡𝑒𝑛𝑐𝑖ó𝑛 𝑑𝑒 𝑣𝑎𝑙𝑜𝑟𝑒𝑠 𝑒𝑛𝑡𝑒𝑟𝑜𝑠 𝑝𝑎𝑟𝑎 𝑙𝑎𝑠 𝑣𝑎𝑟𝑖𝑎𝑏𝑙𝑒𝑠 𝑑𝑒 𝑑𝑒𝑐𝑖𝑠𝑖ó𝑛.
- 11. UNIDAD II En estecontexto resolver el modelo lineal asociado a un modelo de programación entera se conoce frecuentemente como resolver la relajación continua del modelo entero. 𝑬𝑱𝑬𝑹𝑪𝑰𝑪𝑰𝑶 𝟏: 𝑴𝑨𝑰𝑴𝑰𝒁𝑨𝑹 𝒁 = 𝟑𝑿 𝟏 + 𝟒𝑿 𝟐 2𝑋1 + 𝑋2 ≤ 6 2𝑋1 + 3𝑋2 ≤ 9 𝑋𝑖 ≥ 0; 𝑒𝑛𝑡𝑒𝑟𝑜𝑠 𝑫𝑬𝑺𝑨𝑹𝑹𝑶𝑳𝑳𝑶 2𝑋1 + 𝑋2 ≤ 6 X y 0 6 3 0 2𝑋1 + 3𝑋2 ≤ 9 x y 0 3 9/2 0 C= (3, 3/2) 𝑅𝑒𝑠𝑜𝑙𝑣𝑒𝑟 𝑙𝑎𝑠 𝑒𝑐𝑢𝑎𝑐𝑖𝑜𝑛𝑒𝑠 𝑝𝑜𝑟 𝑒𝑙𝑖𝑚𝑖𝑛𝑎𝑐𝑖ó𝑛: (-1) 2𝑋1 + 𝑋2 = 6 2𝑋1 + 3𝑋2 = 9 - 2𝑋1 − 𝑋2 = −6 2𝑋1 + 3𝑋2 = 9 2𝑋2 = 3 𝑋2 = 3 2 𝑋2 = 1,5 𝑍 = 3𝑋1 + 4𝑋2 𝑍 = 12,75
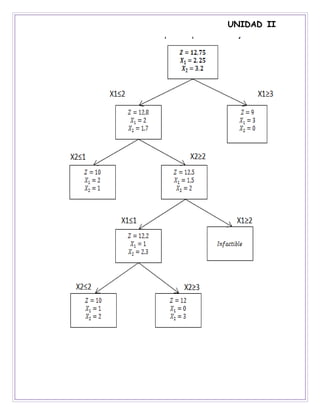
- 12.
- 13. UNIDAD II 𝑆𝑂𝐿𝑈𝐶𝐼Ó𝑁 𝐸𝑁𝑇𝐸𝑅𝐴Z=12; X1=0 X2=3 Cotas: 2𝑋1 + 𝑋2 ≤ 6 𝑋1 ≤ 2,5 2𝑋1 + 3𝑋2 ≤ 9 𝑋1 ≤ 3 𝑋1 ≤ 2 𝑋2 ≤ 1 𝑋2 = 1 𝑋1 = 2 2𝑋1 + 𝑋2 ≤ 6 𝑋1 ≤ 2 2𝑋1 + 3𝑋2 ≤ 9 𝑋1 ≤ 1,5 𝑋1 ≤ 2 𝑋2 ≥ 2 𝑋2 = 2 𝑋1 = 1,52𝑋1 + 𝑋2 ≤ 6 𝑋2 ≤ 4 2𝑋1 + 3𝑋2 ≤ 9 𝑋2 ≤ 2,3 𝑋1 ≤ 2 𝑋2 ≥ 2 𝑋1 ≤ 1 𝑋1 = 1 𝑋2 = 2,3 2𝑋1 + 𝑋2 ≤ 6 𝑋2 ≤ 2 2𝑋1 + 3𝑋2 ≤ 9 𝑋2 ≤ 1,7 𝑋1 ≤ 2 𝑋1 = 2 𝑋2 = 1,7 2𝑋1 + 𝑋2 ≤ 6 𝑋2 ≤ 0 𝑋2 = 0 2𝑋1 + 3𝑋2 ≤ 9 𝑋2 ≤ 1 𝑋1 ≥ 3 𝑋1 = 3 𝑋2 = 0 2𝑋1 + 𝑋2 ≤ 6 𝑋2 ≤ 2 2𝑋1 + 3𝑋2 ≤ 9 𝑋2 ≤ 1,7 𝑋1 ≤ 2 𝑋2 ≥ 2 𝑋1 ≥ 2 𝑋1 = 2 𝑋 = 1 INFACT 2𝑋1 + 𝑋2 ≤ 6 𝑋1 ≤ 2 2𝑋1 + 3𝑋2 ≤ 9 𝑋1 ≤ 1,5 𝑋1 ≤ 2 𝑋2 ≥ 2 𝑋1 ≤ 1 𝑋2 ≤ 2 𝑋2 = 2 2𝑋1 + 𝑋2 ≤ 6 𝑋1 ≤ 1,5 2𝑋1 + 3𝑋2 ≤ 9 𝑋1 ≤ 0 𝑋1 ≤ 2 𝑋2 ≥ 2 𝑋1 ≤ 1 𝑋2 ≤ 3 𝑋2 = 3
- 14. UNIDAD II MINIMIZAR 𝒁= −𝟓𝑿 𝟏 − 𝟖𝑿 𝟐 𝑋1 + 𝑋2 ≤ 6 5𝑋1 + 9𝑋2 ≤ 45 𝑋𝑖 ≥ 0; 𝑒𝑛𝑡𝑒𝑟𝑜𝑠 𝑋1 + 𝑋2 ≤ 6 𝑋1 = 6 𝑋2 = 6 5𝑋1 + 9𝑋2 ≤ 45 X Y 0 5 9 0 −5𝑋1 − 5𝑋2 ≤ −30 5𝑋1 + 9𝑋2 ≤ 45 4𝑋2 ≤ 15 𝑋2 ≤ 3,75 𝑋1 + 3,75 ≤ 6 𝑋1 ≤ 2,25 𝑍 = −41,25
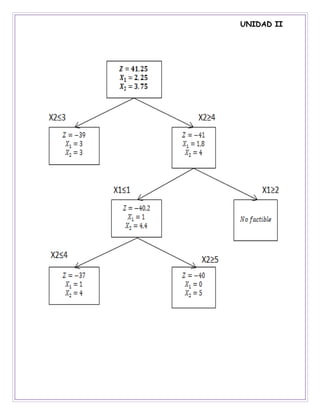
- 15.
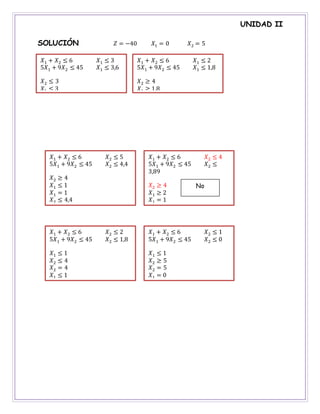
- 16. UNIDAD II SOLUCIÓN 𝑍= −40 𝑋1 = 0 𝑋2 = 5 𝑋1 + 𝑋2 ≤ 6 𝑋1 ≤ 3 5𝑋1 + 9𝑋2 ≤ 45 𝑋1 ≤ 3,6 𝑋2 ≤ 3 𝑋1 ≤ 3 𝑋1 + 𝑋2 ≤ 6 𝑋1 ≤ 2 5𝑋1 + 9𝑋2 ≤ 45 𝑋1 ≤ 1,8 𝑋2 ≥ 4 𝑋1 ≥ 1,8 𝑋1 + 𝑋2 ≤ 6 𝑋2 ≤ 5 5𝑋1 + 9𝑋2 ≤ 45 𝑋2 ≤ 4,4 𝑋2 ≥ 4 𝑋1 ≤ 1 𝑋1 = 1 𝑋2 ≤ 4,4 𝑋1 + 𝑋2 ≤ 6 𝑋2 ≤ 4 5𝑋1 + 9𝑋2 ≤ 45 𝑋2 ≤ 3,89 𝑋2 ≥ 4 𝑋1 ≥ 2 𝑋1 = 1 𝑋2 = 4 No Factible 𝑋1 + 𝑋2 ≤ 6 𝑋2 ≤ 2 5𝑋1 + 9𝑋2 ≤ 45 𝑋2 ≤ 1,8 𝑋1 ≤ 1 𝑋2 ≤ 4 𝑋2 = 4 𝑋1 ≤ 1 𝑋1 + 𝑋2 ≤ 6 𝑋2 ≤ 1 5𝑋1 + 9𝑋2 ≤ 45 𝑋2 ≤ 0 𝑋1 ≤ 1 𝑋2 ≥ 5 𝑋2 = 5 𝑋1 = 0