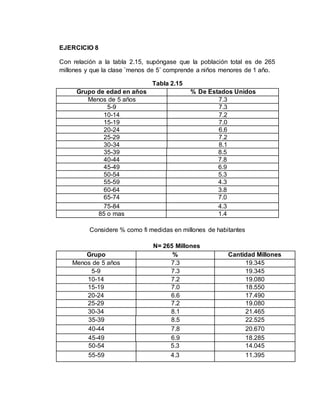
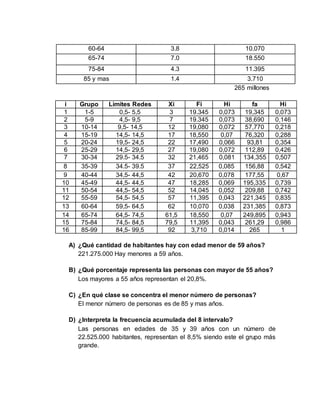
- The document presents data on the population distribution in the United States by age group, with the total population being 265 million people. It includes the percentage and number of people in each age group. - Some key figures extracted from the data include that people under 59 years old account for 221.275 million people, and those over 55 years make up 20.8% of the population. The smallest age group is 85 years and older, with 3.71 million people. 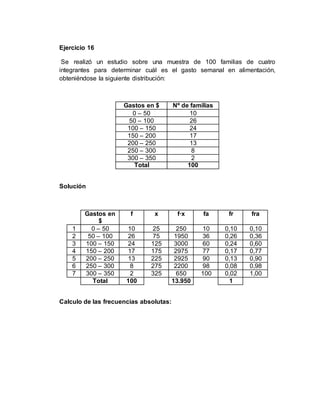- The second part of the document examines survey data from 100 families on their weekly food spending, categorizing the results into spending ranges and calculating statistics like the mean, median and mode.

1. Programa Nacional De Formación En distribución Y Logística
Tablas de frecuencias
UNIDAD 2
Alumna:
Francelismar Valles
Cedula: 29.654.897
Docente:
Efren Escalona
U.C: Estadística
Sección: 2300
Barquisimeto, Agosto 2021

2. EJERCICIO 8
Con relación a la tabla 2.15, supóngase que la población total es de 265
millones y que la clase ¨menos de 5¨ comprende a niños menores de 1 año.
Tabla 2.15
Grupo de edad en años % De Estados Unidos
Menos de 5 años 7.3
5-9 7.3
10-14 7.2
15-19 7.0
20-24 6.6
25-29 7.2
30-34 8.1
35-39 8.5
40-44 7.8
45-49 6.9
50-54 5.3
55-59 4.3
60-64 3.8
65-74 7.0
75-84 4.3
85 o mas 1.4
Considere % como fi medidas en millones de habitantes
N= 265 Millones
Grupo % Cantidad Millones
Menos de 5 años 7.3 19.345
5-9 7.3 19.345
10-14 7.2 19.080
15-19 7.0 18.550
20-24 6.6 17.490
25-29 7.2 19.080
30-34 8.1 21.465
35-39 8.5 22.525
40-44 7.8 20.670
45-49 6.9 18.285
50-54 5.3 14.045
55-59 4.3 11.395

3. 60-64 3.8 10.070
65-74 7.0 18.550
75-84 4.3 11.395
85 y mas 1.4 3.710
265 millones
i Grupo Limites Redes Xi Fi Hi fa Hi
1 1-5 0,5- 5,5 3 19.345 0,073 19,345 0,073
2 5-9 4,5- 9,5 7 19.345 0,073 38,690 0,146
3 10-14 9,5- 14,5 12 19,080 0,072 57,770 0,218
4 15-19 14,5- 14,5 17 18,550 0,07 76,320 0,288
5 20-24 19,5- 24,5 22 17,490 0,066 93,81 0,354
6 25-29 14,5- 29,5 27 19,080 0,072 112,89 0,426
7 30-34 29.5- 34.5 32 21,465 0,081 134,355 0,507
8 35-39 34.5- 39.5 37 22,525 0,085 156,88 0,542
9 40-44 34,5- 44,5 42 20,670 0,078 177,55 0,67
10 45-49 44,5- 44,5 47 18,285 0,069 195,335 0,739
11 50-54 44,5- 54,5 52 14,045 0,052 209,88 0,742
12 55-59 54,5- 54,5 57 11,395 0,043 221,345 0,835
13 60-64 59,5- 64,5 62 10,070 0,038 231,385 0,873
14 65-74 64,5- 74,5 61,5 18,550 0,07 249,895 0,943
15 75-84 74,5- 84,5 79,5 11,395 0,043 261,29 0,986
16 85-99 84,5- 99,5 92 3,710 0,014 265 1
A) ¿Qué cantidad de habitantes hay con edad menor de 59 años?
221.275.000 Hay menores a 59 años.
B) ¿Qué porcentaje representa las personas con mayor de 55 años?
Los mayores a 55 años representan el 20,8%.
C) ¿En qué clase se concentra el menor número de personas?
El menor número de personas es de 85 y mas años.
D) ¿Interpreta la frecuencia acumulada del 8 intervalo?
Las personas en edades de 35 y 39 años con un número de
22.525.000 habitantes, representan el 8,5% siendo este el grupo más
grande.

4. Ejercicio 16
Se realizó un estudio sobre una muestra de 100 familias de cuatro
integrantes para determinar cuál es el gasto semanal en alimentación,
obteniéndose la siguiente distribución:
Gastos en $ Nº de familias
0 – 50 10
50 – 100 26
100 – 150 24
150 – 200 17
200 – 250 13
250 – 300 8
300 – 350 2
Total 100
Solución
Gastos en
$
f x f·x fa fr fra
1 0 – 50 10 25 250 10 0,10 0,10
2 50 – 100 26 75 1950 36 0,26 0,36
3 100 – 150 24 125 3000 60 0,24 0,60
4 150 – 200 17 175 2975 77 0,17 0,77
5 200 – 250 13 225 2925 90 0,13 0,90
6 250 – 300 8 275 2200 98 0,08 0,98
7 300 – 350 2 325 650 100 0,02 1,00
Total 100 13.950 1
Calculo de las frecuencias absolutas:

5. 𝑓𝑎1
= 𝑓1 = 10
𝑓𝑎2
= 𝑓2 + 𝑓𝑎1
= 26 + 36
𝑓𝑎3
= 𝑓3 + 𝑓𝑎2
= 24 + 36 = 60
𝑓𝑎4
= 𝑓4 + 𝑓𝑎3
= 17 + 60 = 77
𝑓𝑎5
= 𝑓5 + 𝑓𝑎4
= 13 + 77 = 90
𝑓𝑎6
= 𝑓6 + 𝑓𝑎5
= 8 + 90 = 98
𝑓𝑎7
= 𝑓7 + 𝑓𝑎7
= 2 + 98 = 100
Calculo de las frecuencias relativas:
𝑓𝑟1
=
𝑓1
𝑛
=
10
100
= 0,10
𝑓𝑟2
=
𝑓2
𝑛
=
26
100
= 0,26
𝑓𝑟3
=
𝑓3
𝑛
=
24
100
= 0,24
𝑓𝑟4
=
𝑓4
𝑛
=
17
100
= 0,17
𝑓
𝑟5
=
𝑓5
𝑛
=
13
100
= 0,13
𝑓
𝑟6
=
𝑓6
𝑛
=
8
100
= 0,08
𝑓
𝑟7
=
𝑓7
𝑛
=
2
100
= 0,02
Calculo de las frecuencias relativas acumuladas:
𝑓𝑟𝑎1
= 𝑓𝑟1
= 0,10
𝑓𝑟𝑎2
= 𝑓𝑟2
+ 𝑓𝑟𝑎1
= 0,26 + 0,10 = 0,36
𝑓𝑟𝑎3
= 𝑓𝑟3
+ 𝑓𝑟𝑎2
= 0,24 + 0,36 = 0,60
𝑓𝑟𝑎4
= 𝑓𝑟4
+ 𝑓𝑟𝑎3
= 0,17 + 0,60 = 0,77

6. 𝑓𝑟𝑎5
= 𝑓𝑟5
+ 𝑓𝑟𝑎4
= 0,13 + 0,77 = 0,90
𝑓𝑟𝑎6
= 𝑓𝑟6
+ 𝑓𝑟𝑎5
= 0,08 + 0,90 = 0,98
𝑓𝑟𝑎7
= 𝑓𝑟7
+ 𝑓𝑟𝑎6
= 0,02 + 0,98 = 1,00
Calculo de la marca clase:
𝑥3 =
𝐿3𝑆
− 𝐿3
2
=
150 − 100
2
= 125
𝑥4 =
𝐿4𝑆
− 𝐿4𝑖
2
=
200 − 150
2
= 175
𝑥5 =
𝐿5𝑆
− 𝐿5𝑖
2
=
250 − 200
2
= 225
𝑥6 =
𝐿6𝑆
− 𝐿6𝑖
2
=
300 − 250
2
= 275
𝑥7 =
𝐿7𝑆
− 𝐿7𝑖
2
=
350 − 300
2
= 325
𝑓
𝑟5
=
𝑓5
𝑛
=
13
100
= 0,13
𝑓
𝑟6
=
𝑓6
𝑛
=
8
100
= 0,08
𝑓
𝑟7
=
𝑓7
𝑛
=
2
100
= 0,02

7. 𝑥3 =
𝐿3𝑆
− 𝐿3
2
=
150 − 100
2
= 125
𝑥4 =
𝐿4𝑆
− 𝐿4𝑖
2
=
200 − 150
2
= 175
𝑥5 =
𝐿5𝑆
− 𝐿5𝑖
2
=
250 − 200
2
= 225
𝑥6 =
𝐿6𝑆
− 𝐿6𝑖
2
=
300 − 250
2
= 275
𝑥7 =
𝐿7𝑆
− 𝐿7𝑖
2
=
350 − 300
2
= 325
Calculo de la media aritmética:
𝑥̅ =
∑ 𝑥𝑖𝑓𝑖
𝑛
=
13950
100
= 139,50
La media es $ 139,50
Calculo de la mediana:
𝑛
2
=
100
2
= 50 → 𝑖 = 3
Gastos en
$
f x f·x fa fr fra
2 50 – 100 26 75 1950 36 0,26 0,36
3 100 – 150 24 125 3000 60 0,24 0,60
𝑀𝑒 = 𝐿𝑖−1 + 𝐴 ∙
𝑛
2
− 𝑓𝑎𝑖−1
𝑓𝑖
𝐿𝑖−1 = 100
𝐴 = 50
𝑓𝑎𝑖−1
= 36
𝑓𝑖 = 24

8. 𝑀𝑒 = 100 + 50 ∙
50 − 36
25
= 128
La mediana es $ 128
Calculo de la moda:
Gastos en
$
f x f·x fa fr fra
1 0 – 50 10 25 250 10 0,10 0,10
2 50 – 100 26 75 1950 36 0,26 0,36
3 100 – 150 24 125 3000 60 0,24 0,60
𝑓 = 26 → 𝑖 = 2
𝑀𝑜 = 𝐿𝑖−1 + 𝐴 ∙
∆𝑓𝑖
∆𝑓𝑖 + ∆𝑓
𝑠
𝐿𝑖−1 = 50
𝐴 = 50
∆𝑓𝑖 = 𝑓𝑖 − 𝑓𝑖−1 = 26 − 10 = 16
∆𝑓
𝑠 = 𝑓𝑖 − 𝑓𝑖+1 = 26 − 24 = 2
𝑀𝑜 = 50 + 50 ∙
16
16 + 2
= 50 + 44 = 90
La moda es $ 90.