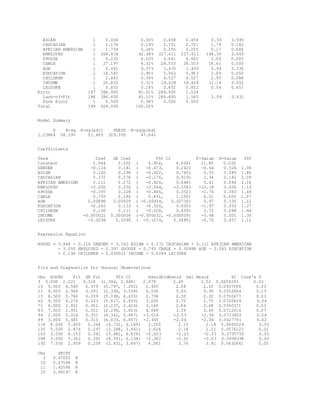
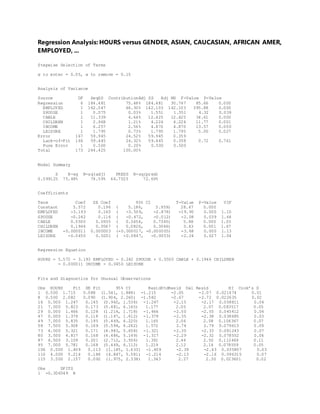
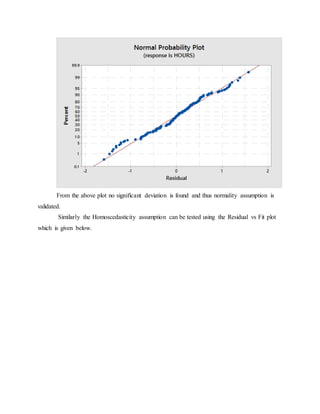
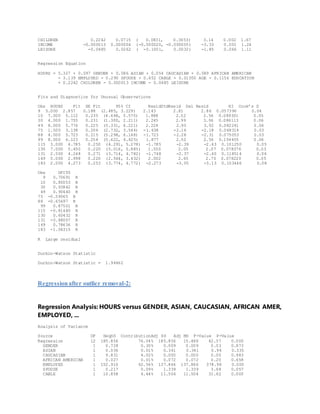
This document describes a regression analysis conducted to predict hours spent watching TV based on various personal factors. Data on gender, race, employment status, marital status, cable access, education, age, number of children, income, and leisure time was collected from random individuals. A correlation matrix and scatter plots showed income had the strongest correlation to TV watching hours. Regression analysis found income was the only statistically significant predictor of viewing time. The analysis aimed to help advertising companies target demographic groups most likely to watch TV.
![HEWLETT-PACKARD
[Type the document title]
[Type the document subtitle]
Surajit Basak
4/16/2015](https://image.slidesharecdn.com/tvwatchingtimeproject-150415164347-conversion-gate01/85/Tv-watching-time-project-1-320.jpg)