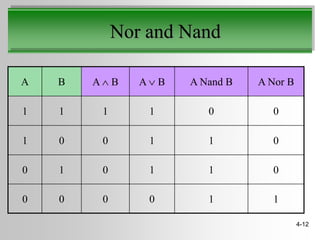
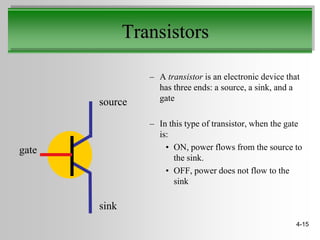
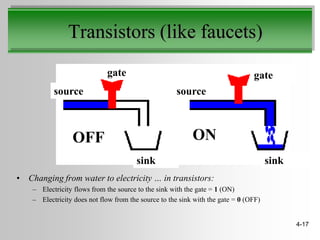
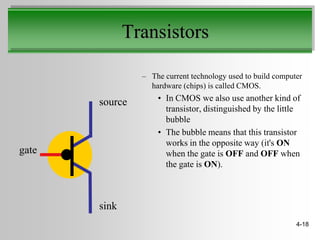
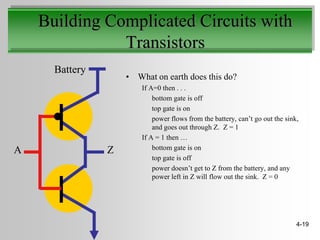
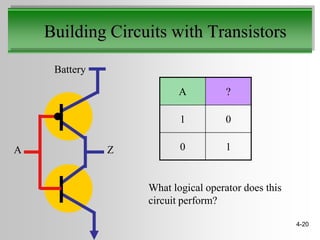
This document discusses truth tables and Boolean logic. It begins by explaining truth tables and how they represent all possible combinations of variable values in Boolean logic sentences. It then provides examples of truth tables for basic logical operators like AND, OR, and NOT. Finally, it discusses how logic circuits are built from transistors to physically represent Boolean logic operations, and provides an example circuit that implements a specific logical operator.

1. TRUTH TABLE
• Remember:
– Decimal to Binary
– Binary to Decimal
– Binary math
– Finish representation of data
• Numbers
• Symbols
• Images
• Audio
• Today:
– Boolean Logic
– Truth Tables
– Circuits
4-1

2. 4-2

3. What we will cover…
• The connection between Boolean logic and circuits
• Boolean (Propositional) Logic
• The design of simple logic circuits
• Representing simple logical sentences in hardware
4-3

4. Logic and Logic Circuits
• What is a circuit?
– the complete path of an electric current, or a collection of electronic
elements
– We are interested in logic circuits, those whose output varies
depending on their input.
• Logic circuits emulate the Boolean logic operators
from propositional logic
4-4

5. Binary for Logic?
• In Propositional Logic we examine the “truth” of
sentences.
– Sentences consist of:
• Variables:
– sub-sentences (A, B, C …) which are either true or false
– In computer science, we use
» true = 1
» false = 0
• Logical Operators:
– e.g., NOT, OR, AND, XOR, NAND, NOR
• Example sentence:
– X = (A AND B) OR C
• We examine the logic of a sentence through “truth table
analysis” 4-5

6. Simplest Truth Table
a Single Variable
• A single variable has only two possible values in
Boolean logic:
– true = 1
– false = 0 A
• A “truth table” represents all of the possible
values of a sentence given the possible values of 1
its inputs (variables).
– We determine the output by considering all possible truth
values for each variable
– we want to see the results of all possible combinations of
0
each variable
• How many rows should appear in a given truth
table? • Example: A = “It is raining” 4-6

7. Logical AND
• Logical AND:
– Takes two variables
– Evaluates to True only if both variables are true
– Written as: (A B)
• Example:
– A = It is raining
– B = I am in London
– (A B) = It is raining and I am in London
– What is the truth table for (A B) ?
• How many combinations of values exist for A AND B?
4-7

8. Logical AND on two variables
It is raining and I
It is raining I am in London
am in London
A B A B
1 1 1
1 0 0
0 1 0
0 0 0
A AND B is true if both A is true and B is true
Otherwise, A AND B is false.
4-8

9. Logical Or
• A OR B
• A B
A B A B
• Has two values: true if either A
or B is true, or if both A and B
1 1 1 are true
• false if they are both false.
1 0 1 • Are either of these things true?
– Note: both can be true… this is not
“exclusive or”
0 1 1
0 0 0
4-9

10. Logical Not
• Used to invert a meaning
• NOT A as an alternative:
A A
• A = “It is raining”
1 0 • A = “It is not raining”
0 1
4-10

11. XOR- Exclusive Or
A B A XOR B • True when either A or B are
true, but not both
1 1 0 • So “A and NOT B” or “B and
NOT A”
1 0 1 • Built from simpler logic:
(A B) ( A B)
0 1 1
0 0 0
4-11

12. Nor and Nand
A B A B A B A Nand B A Nor B
1 1 1 1 0 0
1 0 0 1 1 0
0 1 0 1 1 0
0 0 0 0 1 1
4-12

13. Truth Table Analysis
• How do you build a truth table?
– Step 1: Create columns for all the variables in the sentence
– Step 2: Determine the number of rows you need given the variables in your
sentence
– Step 3: Define all possible sequences (cases) for your truth table, starting
with all variables false and ending with all variables true
– Step 4: Deconstruct the logic in the sentence and fill in your table
– What is the truth table for:
1. X = A AND (NOT B)
2. X = (NOT A) AND (NOT B)
3. X = (A OR B) AND C
4-13

14. Logic and Logic Circuits
• What is a circuit?
– the complete path of an electric current, or a collection of electronic
elements
– we will consider transistors to be the basic building blocks of logic
computer hardware.
– Logic circuits are built from a series of transistors
• What is a transistor?
4-14

15. Transistors
– A transistor is an electronic device that
has three ends: a source, a sink, and a
source gate
– In this type of transistor, when the gate
is:
gate • ON, power flows from the source to
the sink.
• OFF, power does not flow to the
sink
sink
4-15

16. Transistors (like faucets)
The operation of a transistor could be explained by making an analogy to faucets.
• A faucet has:
– An input
• the water company
• “source”
– An output
• a sink (where water is drained)
• “sink”
– Flow control
• If the tap knob (gate) is turned :
– ON water flows from the source to the sink
– OFF no water flows.
• The state of the tap determines the presence of water at the sink
4-16

17. Transistors (like faucets)
gate gate
source source
OFF ON
sink sink
• Changing from water to electricity … in transistors:
– Electricity flows from the source to the sink with the gate = 1 (ON)
– Electricity does not flow from the source to the sink with the gate = 0 (OFF)
4-17

18. Transistors
– The current technology used to build computer
hardware (chips) is called CMOS.
source • In CMOS we also use another kind of
transistor, distinguished by the little
bubble
• The bubble means that this transistor
works in the opposite way (it's ON
gate when the gate is OFF and OFF when
the gate is ON).
sink
4-18

19. Building Complicated Circuits with
Transistors
Battery
• What on earth does this do?
If A=0 then . . .
bottom gate is off
top gate is on
power flows from the battery, can’t go out the sink,
and goes out through Z. Z = 1
If A = 1 then …
A Z bottom gate is on
top gate is off
power doesn’t get to Z from the battery, and any
power left in Z will flow out the sink. Z = 0
4-19

20. Building Circuits with Transistors
Battery
A ?
1 0
A Z 0 1
What logical operator does this
circuit perform?
4-20