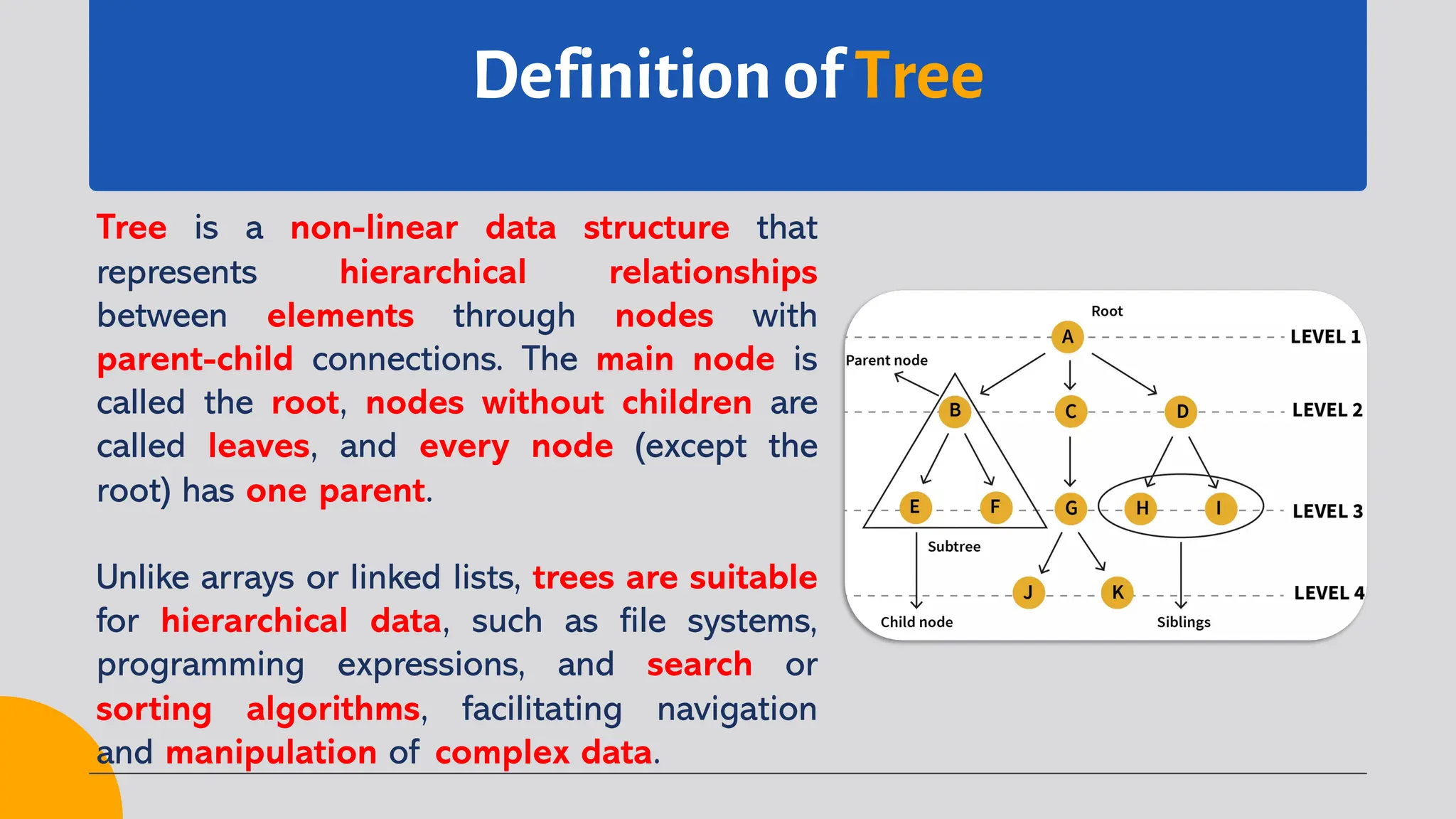
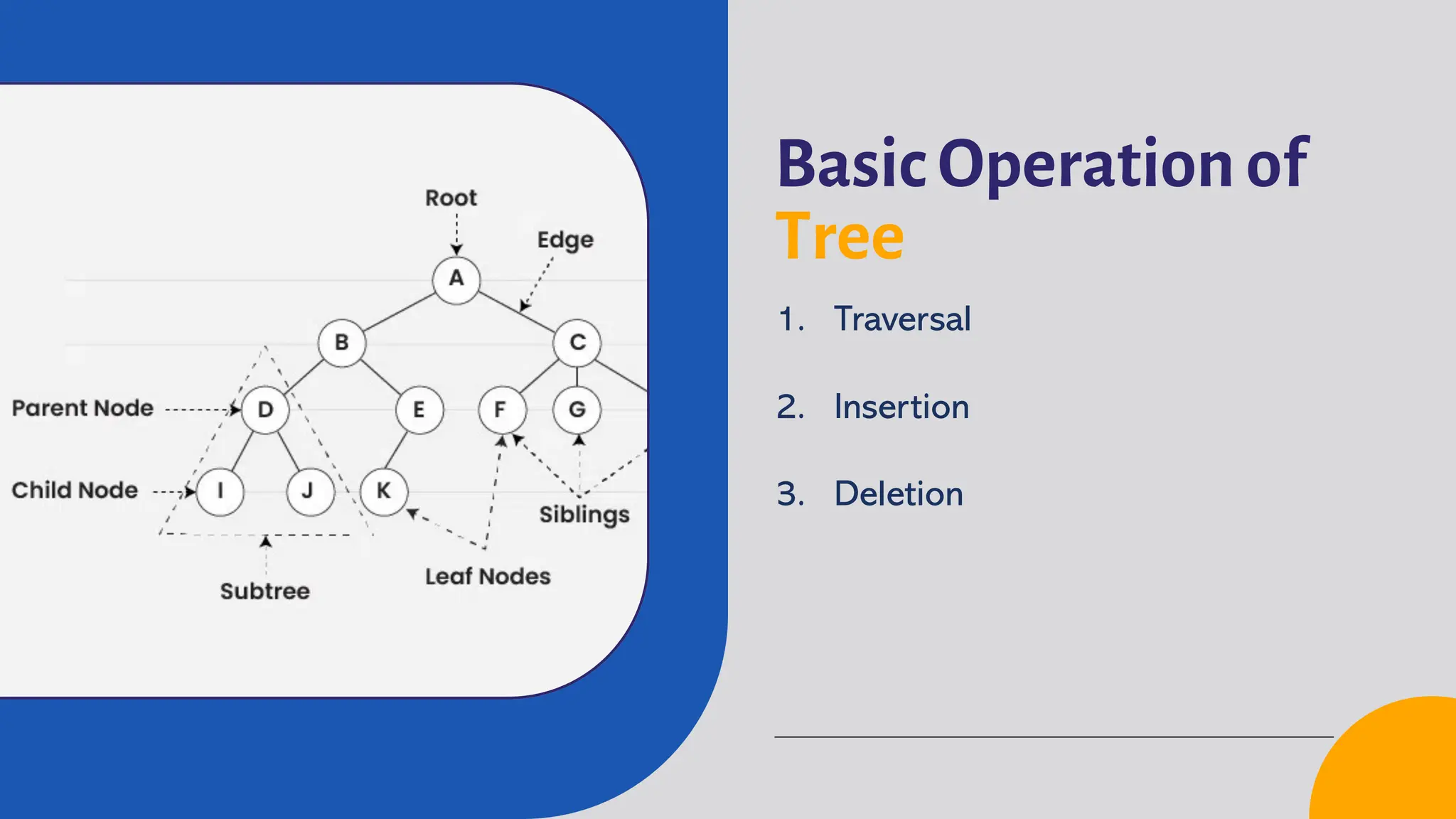
The Tree slide the Data Structures course include: 1. Definition of tree 2. Characteristics of tree 3. Key terms of tree 4. Basic structure of tree 5. Types of tree 6. Basic operation of tree 7. Insertion operation 8. Deletion operation 9. Application of tree 10. Advantages of tree 11. Disadvantages of tree

1. Department of Informatics
Faculty of Industrial Engineering
Universitas Pembangunan Nasional “Veteran” Yogyakarta
Data
Structure
Andi Nurkholis, S.Kom., M.Kom.
Tree: Concept
& Implementation
November 10, 2025

2. Definition of Tree
Tree is a non-linear data structure that
represents hierarchical relationships
between elements through nodes with
parent-child connections. The main node is
called the root, nodes without children are
called leaves, and every node (except the
root) has one parent.
Unlike arrays or linked lists, trees are suitable
for hierarchical data, such as file systems,
programming expressions, and search or
sorting algorithms, facilitating navigation
and manipulation of complex data.

3. Characteristics of Tree
Tree data structure has several characteristics:
ü Consists of nodes that store data.
ü Has a root node as the main node.
ü Every node (except the root) has a parent.
ü Nodes can have children.
ü Nodes without children are called leaves.
ü There are no cycles in a tree.

4. Key Terms of Tree
There are several important terms related to trees:
ü Node: The basic unit in a tree that stores data.
ü Root: The topmost node in a tree; each tree has only one root.
ü Child: A node directly connected below another node.
ü Parent: A node that serves as the parent for nodes below it.
ü Leaf Node: A node that has no children (terminal node).

5. Key Terms of Tree
ü Height of a Node: The longest distance from that node to a leaf node.
ü Depth of a Node: The number of edges between that node and the root.
ü Subtree: A tree structure consisting of a specific node and all of its
descendants.

6. Basic Structure of Tree
The following is a simple representation of a tree:
A (Root)
/
B C
/ /
D E F G
In the example above:
ü Node A is the root.
ü Nodes B and C are children of A, while D, E, F, and G are leaf nodes.

7. Types of
Tree
1. Binary Tree
2. Binary Search Tree (BST)
3. AVL Tree
4. Red-Black Tree
5. N-ary Tree

8. Types of Tree
1. Binary Tree: A tree where each node has a maximum of two children (left
and right). In a binary tree, one of the children may be absent.
2. Binary Search Tree (BST): A type of binary tree where the values of nodes
in the left subtree are always smaller than the node’s value, and the values in
the right subtree are always larger. This facilitates element search.
3. AVL Tree: A type of binary search tree that also maintains balance. Each
node in the tree has a balance factor that must be within the range -1, 0, or
1. This ensures that search, insertion, and deletion operations remain O(log
n).

9. Types of Tree
4. Red-Black Tree: Another type of binary search tree that maintains balance
using color rules for its nodes (red and black). This ensures the tree remains
balanced during various operations.
5. N-ary Tree: A tree where each node can have up to N children. This is more
general and is not limited to two children.

10. Basic Operation of
Tree
1. Traversal
2. Insertion
3. Deletion

11. Traversal Operation
Traversal is a method to visit each node in a tree. There are several ways to
traverse a tree:
ü Pre-order Traversal: Visit the node, then the left subtree, followed by the
right subtree.
ü In-order Traversal: Visit the left subtree, the node, then the right subtree.
(Useful for Binary Search Trees to obtain sorted elements)
ü Post-order Traversal: Visit the left subtree, the right subtree, then the node.
ü Level-order Traversal: Visit each level of the tree from top to bottom.

12. Insertion Operation
Inserting a new node into a tree depends on the type of tree. Below is a
description of the steps for insertion in a tree data structure (e.g., binary tree):
ü Start from the root.
ü Compare the value with the current node.
ü Move to the left subtree if smaller, or the right subtree if larger.
ü Find an empty position.
ü Insert the new node as a child and update the parent-child relationship.

13. Deletion Operation
Below is a description of the steps for deletion in a tree (e.g., Binary Search
Tree – BST):
ü Start from the root and locate the node to be deleted.
ü Determine the case: leaf, one child, or two children.
ü If it is a leaf, delete it directly.
ü If it has one child, link the child to the parent node.
ü If it has two children, replace it with its predecessor or successor, then
delete the replacement node, ensuring the tree structure remains valid.

14. Application of
Tree
1. Hierarchical Representation
2. Databases & Indexing Systems
3. Expression Processing in
Computing
4. Artificial Intelligence and Search
Algorithms
5. Data Compression

15. Application of Tree
1. Hierarchical Representation: Trees effectively represent hierarchical data,
such as file systems, corporate organizations, family trees, or XML/HTML
documents, facilitating navigation, grouping, and data management.
2. Databases and Indexing: Trees, such as B-Trees and B+ Trees, are used in
DBMS for indexing, speeding up data search, insertion, and deletion, and
optimizing disk access in large databases.
3. Expression Processing: Binary trees are used for parsing and evaluating
expressions, with internal nodes as operators and leaves as operands,
making infix-to-postfix conversion and compilation optimization easier.

16. Application of Tree
4. Artificial Intelligence and Search: Trees are used to model the state space
in search algorithms, such as search trees and decision trees, aiding problem
solving, game AI, as well as classification and prediction in machine learning.
5. Data Compression: Trees, such as Huffman Trees, are used in Huffman
Coding to assign variable-length binary codes based on symbol frequency,
enabling efficient data compression in files like JPEG, MP3, and ZIP.

17. Advantages of Tree
1. Efficient Data Organization: Trees help organize data hierarchically and
efficiently.
2. Fast Access: Search, insertion, and deletion operations can be performed
efficiently (O(log n) for a balanced BST).
3. Facilitates Data Traversal: Provides various ways to visit and manipulate
data.

18. Disadvantages of Tree
1. Memory: Requires more memory compared to linear data structures like
arrays.
2. Balanced Load: The performance of a tree depends on how balanced it is.
An unbalanced tree can degrade performance to O(n).

19. Department of Informatics
Faculty of Industrial Engineering
Universitas Pembangunan Nasional “Veteran” Yogyakarta
Andi Nurkholis, S.Kom., M.Kom.
November 10, 2025
Done
Thank
You