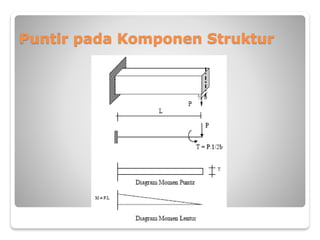
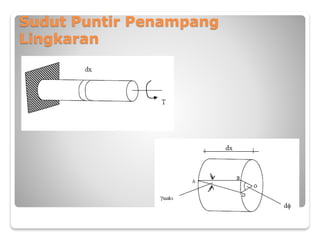
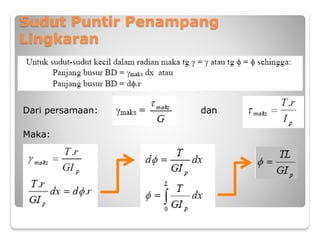
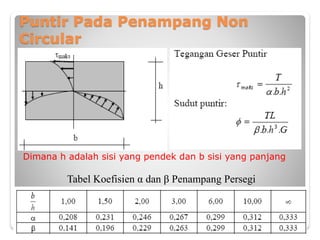
Dokumen tersebut membahas tentang torsi pada bahan dan komponen struktur. Secara umum, torsi terjadi ketika suatu balok atau kolom berputar terhadap sumbunya yang dapat disebabkan oleh beban yang tidak berada pada sumbu simetri. Dokumen tersebut menjelaskan tentang tegangan geser torsi, sudut torsi, dan analisis torsi pada berbagai penampang seperti lingkaran dan bukan lingkaran. Beberapa contoh perhit