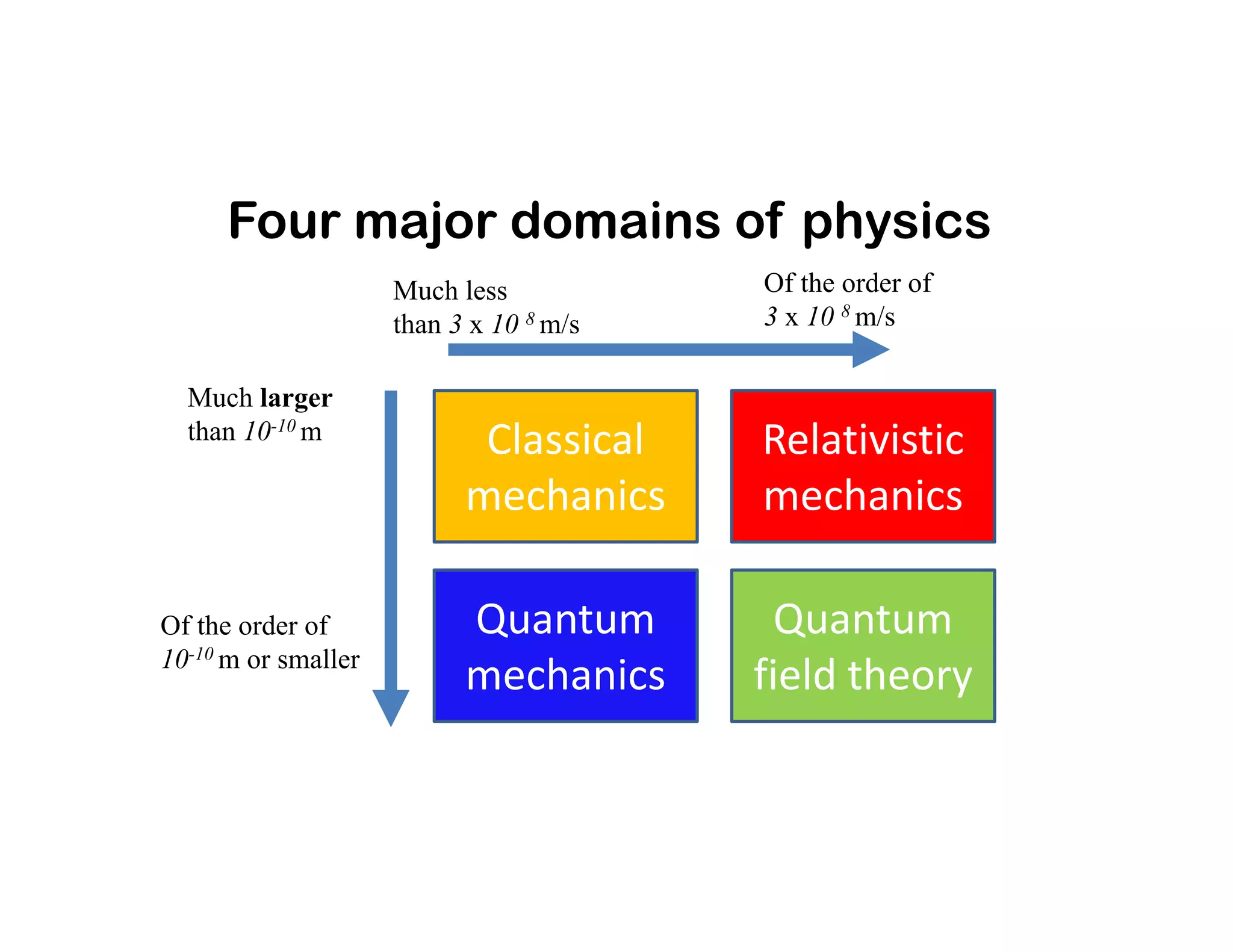
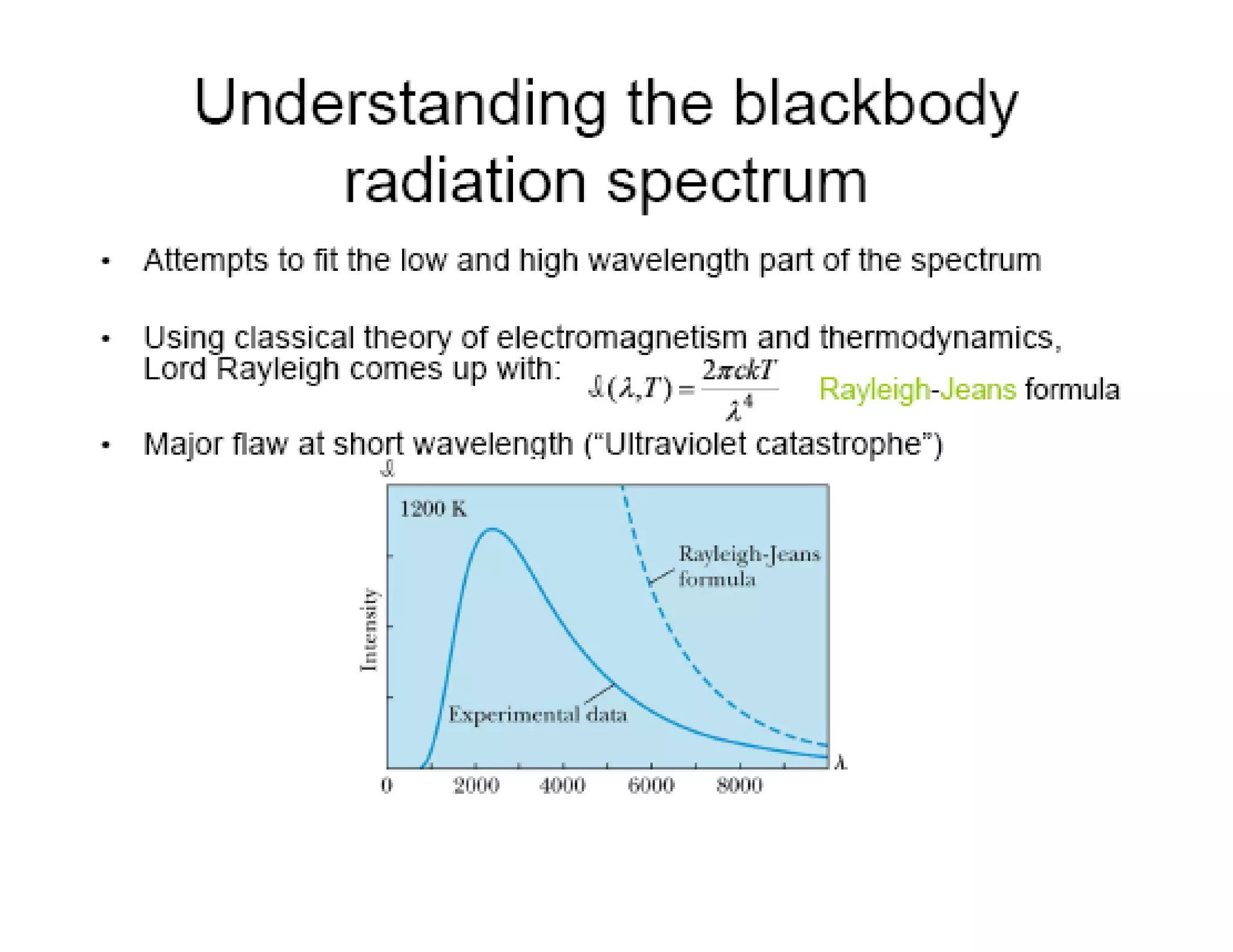
Planck introduced the concept of quanta to explain blackbody radiation. Classical physics predicted radiation energy would increase indefinitely with frequency, but observations showed it plateauing then dropping off sharply. Planck hypothesized radiation was emitted and absorbed in discrete "quanta" of energy proportional to frequency. This resolved the ultraviolet catastrophe and fit empirical data, establishing quantum theory. Later, Einstein extended quanta to explain the photoelectric effect, lending strong support to Planck's hypothesis and the particle-like nature of electromagnetic waves. These developments marked the birth of quantum physics replacing classical concepts.

1. Four major domains of physics
Classical
mechanics
Quantum
mechanics
Relativistic
mechanics
Quantum
field theory
Much larger
than 10-10 m
Of the order of
10-10 m or smaller
Much less
than 3 x 10 8 m/s
Of the order of
3 x 10 8 m/s

2. Quantum Mechanics
(The physics of the microscopic world)
1.Introduction to Quantum Mechanics, by D. J. Griffiths
2.Introduction to Quantum Mechanics, by C. W. Sherwin
3.Quantum Mechanics: An Introduction, by W. Greiner
4.The Feynman Lectures on Physics, Volume III
5.Lecture Notes and Problems Bank, by R. S. Saraswat
and G. P. Sastry,
6. Physics I: Oscillations and Waves, by S. Bharadwaj
and S. P. Khastgir,
References:

3. 3
Evolution in Mechanics
@Citizendium

4. Classical concept
Two distinct categories :
1. Material body (particle)
Newton’s laws of motion
2. Electromagnetic field (wave)
Maxwell’s equation
Additionally
Laws of thermodynamics
Fundamental constants :
1. velocity of light c
2. Avogadro Number N
3. Boltzman constant k
4. Unit of charge e
Position and velocity (momentum) are
precisely measurable
Spread over the space, amplitude gives
energy/intensity, frequency is nothing
but time periodicity of oscillator
E = kT
E = mc2
Velocity << c : non-relativistic
Velocity comparable to c : relativistic

5. Classical concepts never allow to think that
1. Wave may also behave like particle.
(Planck’s hypothesis)
2. Particle may behave like wave.
(de Broglie hypothesis)
3. Position and momentum of a particle cannot
be measured accurately simultaneously.
(Heisenberg uncertainty principle)
4. Energy of wave is related with frequency
and quantised.
These new concepts are basically quantum concepts

6. Wave‐particle duality
Dr. T. K. Nath
Is light consists of particles or waves?
Interference, Diffraction Phenomena
proves wave nature of light

7. EARLY 19TH CENTURY
Dr. T. K. Nath

8. Planck’s theory of Black body radiation (1900)
Photoelectric effect by Einstein (1904)
Compton effect by Compton (1920)
Dr. T. K. Nath

9. •Theory of Black body radiation (Planck 1900)
•Photoelectric effect (Einstein 1905)
•Atomic Structure and Spectroscopy (Bohr 1913)
•Compton effect (Compton 1920)
Failures of Classical Physics
The Experimental Basis of Quantum Mechanics
lies in the
Quantum Mechanics – A New Interpretation of Nature

10. Birthday
of
Quantum Physics
on
14th December, 1900
On this date German physicist Max
Planck first presented his new
quantum concepts.
Max Karl Ernst Ludwig Planck
1858-1947

h
E 
Planck introduces a new
fundamental constant h
to explain black-body radiation

11. Experiments
1. Photoelectric effect
(1921, Einstein) (eV)
2. Compton effect
(1927, Compton) (k eV)
3. Pair Production
(1948, Patrick Blackett)(M eV)
Waves behaving as particles Particles behaving as waves
Electron diffraction
Davisson –Germer (USA)
and Thompson (UK) (1927)
Electron microscope
Experiments
Quantum Physics
Dual Nature
Black Body radiation
Frank Hertz Expt
Discrete energy level Concept of Spin
Stern Gerlach Expt
https://mmpant.com/2020/04/09/quantum‐mechanics‐in‐everyday‐life/

12. Timeline for the evolution/understanding of quantum phenomenon
Experiments on blackbody radiation Photoelectric effect
Franck Hertz experiment Davission Germer experiment
Stern Gerlach experiment
……
Theoretical development : Schrodinger’s and Heisenberg’s picture
High energy physics
Quantum optics
Statistical physics
Biophysics
Condensed matter physics

13. An ideal black body is an empty cavity whose walls are maintained
at a given temperature T (at thermodynamic equilibrium)
BLACKBODY RADIATION
The mother of Quantum Physics

14. Any object with a temperature above absolute zero emits
electromagnetic radiation at all wavelengths. If the object is
perfectly black (so it doesn't reflect any light), then the radiation
that comes from it is called blackbody radiation.
1. Blackbody Radiation

15. Blackbody:
Which absorbs all the radiation .
Total energy = absorbed+ reflected+ transmitted;
Eg: Two body are very close to BB;
Lamp black; a=0.96; and
Platinum black, a=0.98
Radiation:
Irreversible flow of energy away from the source, the energy per unit time
is transported out to infinity and never comes back.
A charge at rest or a steady current does NOT generate EM wave
Accelerating charge (changing current ) produces EM wave
Thermal Radiation from the Human Body:
The radiation is in the infrared region of the spectrum close to 7-15 m.
So, the thermal imaging device for human are most sensitive in this
range. eq: scanner placed at the airport during checking.

16. 0 0.5 1 1.5 2 2.5 3 3.5 4
[Hz] 1014
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
10-17
1,peak
2,peak
3,peak
T
1
= 1000 K
T
2
= 1400 K
T
3
= 1800 K
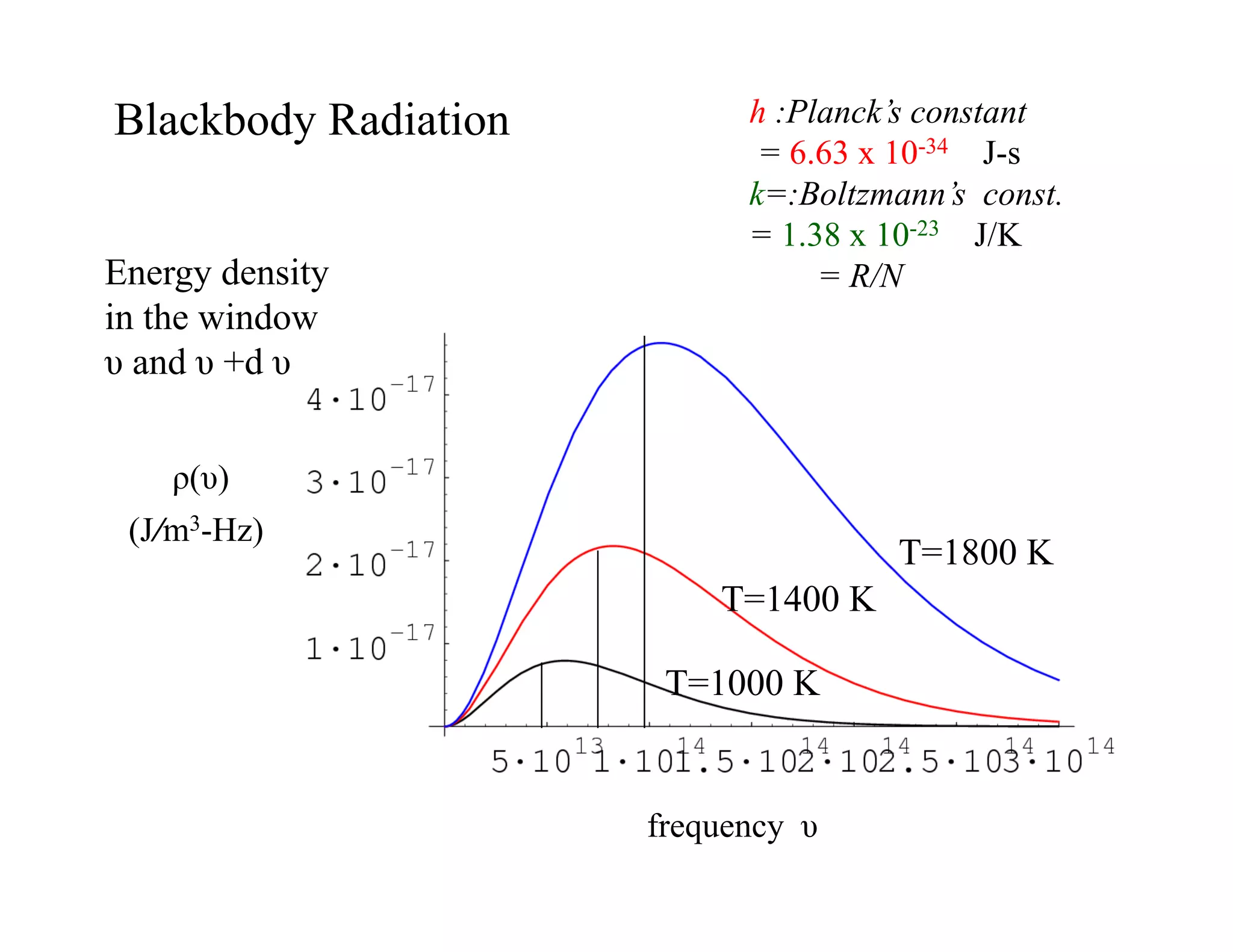
One of the main
challenges was to
explain the
spectrum of
blackbody
radiation from
classical
concepts
Observed spectral density of the black body radiation
vs. frequency at different temperature

18. Blackbody Radiation
T=1000 K
T=1400 K
T=1800 K
ρ(υ)
(J/m3-Hz)
Energy density
in the window
υ and υ +d υ
frequency υ
h :Planck’s constant
= 6.63 x 10-34 J-s
k=:Boltzmann’s const.
= 1.38 x 10-23 J/K
= R/N

19. BLACKBODY RADIATION
Dr. T. K. Nath

20. BLACKBODY RADIATION
The mother of Quantum Physics
According to classical electrodynamics
such a cavity has infinite number of
normal modes. There is no upper limit to
the frequency of these normal modes
As there is no upper limit to the frequency
of these normal modes, there would be
infinite number of normal modes, and thus
infinite amount of energy residing in the
EM radiation within the cavity at a finite
temperature.
Ultraviolet catastrophe

21. Classical theory of Rayleigh-Jeans law
The amount of energy per unit volume per unit frequency interval (Spectral
density) should increase with frequency as 2. (Obeyed well at low frequencies)
T=1800 K
T=1400 K
T=1000 K
T=1800 K
frequency υ
ρ(υ)

22. ρ(υ)
frequency υ
T=1800 K
υ dependence
2

23. Simple assumption that the radiators (walls) are simple harmonic
oscillators. As classical physics predicted from the law of equipartition
energy theorem, that average energy of the oscillators is kBT ,
then the spectral energy density
= no. of standing wave modes in the cavity in the frequency range
 and +d × average energy of the oscillators (radiation field)
×
Classical theory of Rayleigh-Jeans

25. Ultraviolet catastrophe !!!

26. Rayleigh-Jeans law
Planck’s law
ρ(υ)
frequency υ

27. Rayleigh-Jeans law
(Classical theory)
T=1800 K
T=1400 K
T=1000 K
T=1800 K
frequency υ
ρ(υ)
2 dependence
T=1800 K

28. 
h
E 
Quantum energy of photon
h= Planck’s constant
=6.626x10-34 Jsec
: frequency of radiation
Max Karl Ernst Ludwig Planck
1858-1947
Dr. T. K. Nath

29. Planck’s Radiation Law
5
8 1
( , )
1
hc
kT
hc
E T
e



 

The density of radiant energy in the cavity per unit
wavelength interval, at the wavelength , and at the
temperature T
Dr. T. K. Nath

30. Planck’s postulate
Any physical entity with one degree of freedom and whose ``co-ordinate” is
oscillating sinusoidally with frequency  can possess only total energies E as
integral multiple of h.
E = 0
2
4
Classical
h = Planck’s constant

37. Planck's law of black body radiation (1900)
Planck’s assumption (1900):
Radiation of a given frequency ν
could only be emitted and
absorbed in “quanta” (discrete
bundles) of energy
h =6.626x10-34 J-sec
(Planck’s constant)
: frequency of radiation
E=hν

38. Planck’s Formula
Rayleigh-Jeans law

39. Large
>>
 ‐
In the high frequency region
it falls down exponentially with increasing
frequency, again in agreement with
the black body radiation data
0 0.5 1 1.5 2 2.5 3 3.5 4
[Hz] 10
14
0
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
10
-17
1,peak
2,peak
3,peak
T
1
= 1000 K
T
2
= 1400 K
T
3
= 1800 K

40. High frequency region in the BBR:
Low frequency region in the BBR
)
10
9
.
2
(
, 3
max K
m
b
T 


 


41. Experiments
1. Photoelectric effect (1902)
2. Compton effect (1922)
3. Pair Production
Waves behaving as particles
Quantum Physics

42. Albert Einstein
(1879-1955)
Photoelectric Effect
in 1905
Dr. T. K. Nath

43. Photoelectric effect
Dr. T. K. Nath