The document discusses time and space complexity analysis for algorithms, including using Big O notation to describe an algorithm's efficiency. It provides examples of time complexity for different codes, such as O(n) for a simple loop and O(n^2) for a double loop. The document also covers space complexity and how to estimate the complexity of a problem based on input size constraints.

2. Time and Space Complexity
Analysis

3. Time Complexity
It is a measure of time taken by an algorithm to run as a function of the input size.
Here time taken is in terms of number of operations processed by computer.
We use different notations while determining time complexity, most common being
O-notation.
O-notations describe the number of operations performed in the worst case.
We will use O-notation for time and space complexity analysis.

4. While determining complexity, we assume input size is large, so we
consider the highest degree term, and ignore other terms and constants.
We also ignore the constant coefficients.
For example, for input size n, an algorithm performs 3*n3+5*n2+2*n+7
operations.
Its time complexity will be O(n3).

6. Example Codes:
1.
In this code, n operations are formed. So time complexity is O(n).
2.
In the above code, we are using double for loops.
When i=0, the inner loop performs n-1 operations.
When i=1, the inner loop performs n-2 operations.
.
When i=n-2, the inner loop performs 1 operation.
So, the number of operations performed: 1 + 2 + 3 + … (n-1) = n2/2 - 3*n/2 + 2
So, Its time complexity will be O(n2).
for(int i=1;i<=n;++i){
pre[i]=pre[i-1]+a[i];
}
for(int i=0;i<n;++i){
for(int j=0;j<n-i-1;++j){
if(a[j+1]<a[j])
swap(a[j],a[j+1]);
}
}

7. 3.
In this code, the search space is reduced by a factor of 2 in each iteration.
So, the number of operations performed will be ceil(log2n). And thus, time complexity is O(log2n).
4.
// binary search 60 , 30 , 15 , 7 , 3 , 1
int st=1,en=n;
while(st<=en){
int mid=(st+en)/2;
if(a[mid]==value)
return true;
if(a[mid]>value)
en=mid-1;
else
st=mid+1;
}
return false;
for(int i=1;i<=n;++i){
for(int j=1;j<=n;j+=i){
// code
}
}

8. 4.
In the above code, we are using double for loops.
When i=1, the inner loop performs n operations.
When i=2, the inner loop performs n/2 operations.
When i=3, the inner loop performs n/3 operations.
.
When i=n, the inner loop performs 1 operation.
So, the number of operations performed: n/1 + n/2 + n/3 … + 1 = n*(1 + 1/2 + 1/3 + 1/4 +.. + 1/n) <= n*log2n
So, time complexity is O(n*log2n).
for(int i=1;i<=n;++i){
for(int j=1;j<=n;j+=i){
// code
}
}
5.
Time complexity is O(1).
// Sum of first n natural numbers.
ans=n*(n+1)/2;

9. Estimating the intended time complexity of a problem by looking at its constraints
Most computer processors and online judges can process 108 operations per second.
So, we can determine the complexity of the algorithm to be used by observing constraints on input size.
For n=1018 , O(1) or O(log2n) algorithms may be used.
For n=1010 , O(√n) algorithms may be used.
For n=107 , O(n) algorithms may be used.
For n=106 , O(n) or O(n*log2n) algorithms may be used.
For n=105 , O(n) , O(n*√n) , O(n*log2n) or O(n*log2n*log2n) algorithms may be used.
For n=5000 , O(n2) algorithms may be used.
For n=2000 , O(n2) or O(n2 * log2n) algorithms may be used.
For n=500 , O(n3) algorithms may be used.
For n=100 , O(n4) algorithms may be used.
For n=40 , O(n*2n/2) algorithms may be used.(using meet-in-middle)
For n=24 , O(2n) algorithms may be used.
For n=18 , O(n*2n) algorithms may be used.

10. Space Complexity:
It is a measure of memory consumed by an algorithm as a function of input size.
It can also be represented in O-notation.
For example:
Its space complexity is O(1).
Its space complexity is O(n).
Its space complexity is O(n2).
Its space complexity is O(n*m).
int arr[n][n];
int arr[n][m];
int arr[n];
int a=1,b=2,c=3;

11. int data type (or int32_t) takes 4 bytes.
long long int (or int64_t) takes 8 bytes.
short int (or int16_t) takes 2 bytes.
char,bool,int8_t data type takes 1 byte.
In Online Judges, memory is measured in MB.
Most of the time, 50 MB memory is allowed in OJs.
(memory consumed by an array of 107 integers is 40 MB).
By observing constraints on input size, we can determine space complexity.
Important : If we declare an array of 106 integers in the main function, we will get a runtime error. But,
we can declare it globally.
There is no such issue for vectors.

12. #include<bits/stdc++.h>
using namespace std;
int main(){
mt19937 rng((unsigned int) chrono::steady_clock::now().time_since_epoch().count());
auto start=chrono::high_resolution_clock::now();
// your code here
auto stop=chrono::high_resolution_clock::now();
auto duration=chrono::duration_cast<chrono::microseconds>(stop-start);
cerr<<duration.count()/1000.0<<" msn";
}

13. STANDARD TEMPLATE
LIBRARY
(STL)
The C++ STL (Standard Template Library) is a powerful set of C++
template classes to provide general-purpose classes and functions
with templates that implement many popular and commonly used
algorithms and data structures like vectors, lists, queues, and
stacks.
STL has four components
1) Algorithms 2)Containers 3)Functions 4)Iterators

14. Algorithms
The header algorithm defines a collection of functions especially designed to be used on ranges of
elements. They act on containers and provide means for various operations for the contents of the
containers.
• Algorithms
• sort(first_iterator, last_iterator) - To sort the given vector/array
• reverse(first_iterator, last_iterator) - To reverse a vector/array
• *max_element(first_iterator, last_iterator) - To find the maximum element of a vector/array
• *min_element(first_iterator, last_iterator) - To find the minimum element of a vector/array
• count(first_iterator, last_iterator) - To count the occurrences of x in vector/array
• find(first_iterator, last_iterator, x) – Returns an iterator to the first occurence of x in vector and points to
last address of vector ((name_of_vector).end()) if element is not present in vector
• lower_bound(first_iterator, last_iterator, x) – returns an iterator pointing to the first element in the range
[first,last) which has a value not less than ‘x’.
• upper_bound(first_iterator, last_iterator, x) – returns an iterator pointing to the first element in the range
[first,last) which has a value greater than ‘x’.
• next_permutation(first_iterator, last_iterator) – This modified the vector to its next permutation
• distance(first_iterator,desired_position) – It returns the distance of desired position from the
first iterator.This function is very useful while finding the index

15. Containers
Containers or container classes store objects and data. There are in total seven
standard “first-class” container classes and three container adaptor classes and only
seven header files that provide access to these containers or container adaptors.
• Containers
• Vector : vector is a class that creates a dynamic array allowing insertions and deletions at the back
• Set : set is an associate container for storing unique sets
• Multiset : Multiset is an associate container for storing non- unique sets
• Map : Map is an associate container for storing unique key-value pairs, i.e. each key is associated
with only one value(one to one mapping)
• Multimap : multimap is an associate container for storing key- value pair, and each key can be
associated with more than one value
• Stack : It follows last in first out(LIFO)
• Queue : It follows first in first out(FIFO)
• Priority queue : First element out is always the highest priority element
• List : list is the sequence containers that allow the insertions and deletions from anywhere
• Deque : deque is the double ended queue that allows the insertion and deletion from both the ends

16. ITERATORS
Iterators are used to point at the
memory addresses of STL containers.
They are primarily used in sequence of
numbers, characters etc. They reduce
the complexity and execution time of
program.
Operations of iterators :-
1. begin() :- This function is used to
return the beginning position of the
container.

17. PAIRS
A PAIR IS A SIMPLE CONTAINER WHICH CONSISTS OF TWO ELEMENTS OR OBJECTS. THE FIRST
ELEMENT IS REFERENCED AS ‘FIRST’ AND THE SECOND ELEMENT AS ‘SECOND’ AND THE ORDER IS
FIXED (FIRST, SECOND). IT
IS USED TO COMBINE TOGETHER TWO VALUES WHICH MAY BE DIFFERENT IN TYPE AND PROVIDES
A WAY TO STORE TWO HETEROGENEOUS OBJECTS AS A SINGLE UNIT.
DECLARING A PAIR:
PAIR <DATA_TYPE1,DATA_TYPE2> PAIR_NAME;
ASSIGNING VALUES:
METHOD 1:
PAIR_NAME.FIRST = VALUE_1;
PAIR_NAME.SECOND = VALUE_2;
METHOD 2:
PAIR_NAME = MAKE_PAIR(VALUE_1,VALUE_2);
LOGICAL OPERATORS CAN ALSO BE USED TO COMPARE PAIRS. VECTOR OF PAIRS CAN ALSO BE USED LIKE
THIS :
VECTOR <PAIR<INT,INT>> V;

18. SOME LINKS
HTTPS://WWW.GEEKSFORGEEKS.ORG/CPP-STL-TUTORIAL/
HTTPS://WWW.YOUTUBE.COM/WATCH?V=LYGLTMAWEPS&LIST=PLK6
CEY9XXSIA-XO3HRYC3M0AITZDUT7AA
https://www.youtube.com/watch?v=EtCml4TWqW0&list=PL2q4fbVm1Ik4O
Wga4UQR4WlYteMiH46zG

19. Sorting with comparator
function

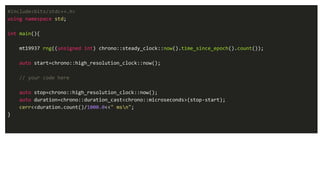
20. Basic sorting:
We compare i-th element with j-th element. Every time we find a smaller element (v[j]) than
v[i], we swap them. Time complexity is (n*n).

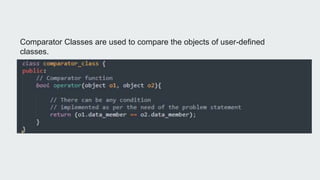
21. Using comparator in basic sorting:
We have defined a boolean function which will return true if v[i]>v[j]. That means we have to
swap them, and if it returns false that means v[i] is less than or equal to v[j].

22. Comparator Classes are used to compare the objects of user-defined
classes.

23. sort() function in c++
The algorithm used by sort() is IntroSort. Introsort being a hybrid
sorting algorithm uses three sorting algorithm to minimize the running
time, Quicksort, Heapsort and Insertion Sort. Simply putting, it is the
best sorting algorithm around. It is a hybrid sorting algorithm, which
means that it uses more than one sorting algorithms as a routine.
For sorting in ascending order we use:
sort ( my_vector.begin() , my_vector.end() );

24. Using comparator in sort() function in c++
We have 2 methods to sort in descending order:
1. Sort in ascending order and then reverse it.
sort ( my_vector.begin() , my_vector.end() );
reverse ( my_vector.begin() , my_vector.end() );
2. Using inbuilt function
sort ( my_vector.begin() , my_vector.end() , greater<int>() );
greater<int>() is a inbuilt comparator function.

25. Using comparator function to sort
Descending order Ascending order
Notice that there is a very small difference between both cmp functions. In descending order
we are checking if v[i]>v[j] and opposite(v[i]<v[j]) in ascending order.

26. Comparator in set Comparator in priority queue
Instead of using a comparator function, we use comparator class in containers like set, priority
queue, maps, etc.

27. Q1
Given a vector of string, Sort the vector elements on the basis of
size of strings in descending order. If sizes are equal, sort them in
lexicographically smallest order.
For example:
Given: [abc, o, tdc, zx, d, za]
Output: [abc, tdc, za, zx, d, o]

28. Q2
Given a vector of pair of non negative integers, Sort the vector
elements on the basis of second element of pairs in descending
order. If first elements are equal, sort them on the basis of first
element of pairs in ascending order
For example:
Given: [(11,11),(5,13),(25,7),(5,18),(3,13)]
Output: [(5,18),(3,13),(5,13),(11,11),(25,7)]

29. Q3
Given a list of non negative integers, arrange them such that they
form the largest number.
For example:
Given [3, 30, 34, 5, 9], the largest formed number is
9534330.
Given [1, 17, , 52, 9], the largest formed number is
952171.
Question link

30. Practice Problems Workshop 1
Codigo
(In Code We Trust)
Time complexity
1. Practice problems
STL
1. Practice Problems
2. Problem2
Sorting
1. Problem1
2. Problem2
3. Problem3
4. Problem4
Sorting with comparator
function
1. Problem1
2. Problem2
3. Problem3
4. Problem4
5. Problem5