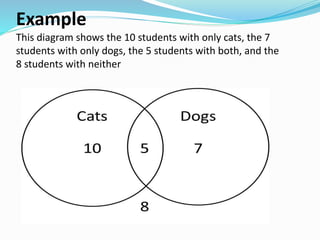
The document discusses objectives for learners across three domains: cognitive, affective, and psychomotor. In the cognitive domain, learners will illustrate set operations like union, intersection, and difference through examples with sets A, B, and C. In the affective domain, learners will discuss real-life applications of well-defined sets and their properties. In the psychomotor domain, learners will create Venn diagrams to represent sets, subsets, and set operations like those showing students with cats and/or dogs.

2. COGNITIVE DOMAIN
Objective:
In 30 minutes of discussion, the
learners will be able to illustrate
the union and intersection of sets
and the difference of two sets.

3. Example
 Intersection of Sets
The intersection of sets A
and B, written as A ∩ B, is
a set of the elements that
are members of both A
and B.
Given:
 A= {1,2,3,4,5,6,},
 B= {2,4,6}
 C= {1,3,5,…}
Find:
a. A ∩ B
b. A ∩ C
c. B ∩ C

4. AFFECTIVE DOMAIN
Objective:
In 30 minutes of discussion, the
learners will be able to value in
real life situations the well-
defined sets, subsets, universal
sets, null sets and cardinality of
sets.

5. Example
 State whether each of
the following sets is well
defined or not. Explain.
 1. The set of nice people.
 2. The set of good
teachers.
 3. The set of multiples of

6. PSYCHOMOTOR DOMAIN
Objective:
 In the 30 minute discussion the
learners will be able to create Venn
diagram to represent sets, subsets
and set operations

7. Example
This diagram shows the 10 students with only cats, the 7
students with only dogs, the 5 students with both, and the
8 students with neither