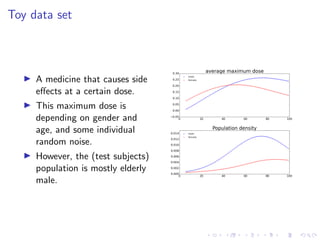
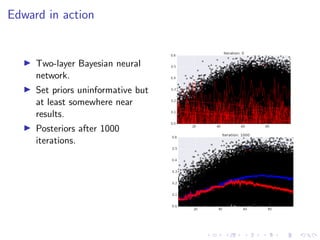
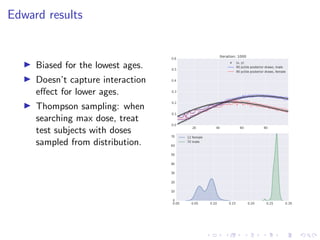
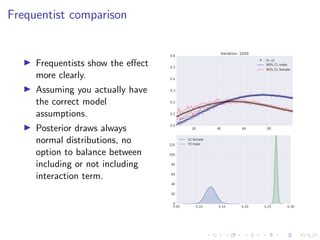
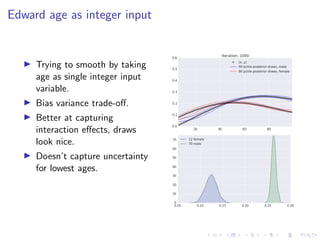
The document discusses Thompson Sampling, a strategy for addressing the multi-armed bandit problem, particularly in data science and marketing contexts. It highlights the historical development and applications of Thompson Sampling, including its use in clinical trials and Bayesian modeling. The conclusion emphasizes the importance of data acquisition costs and advocates for the integration of Thompson Sampling in strategic data collection and modeling efforts.

1. Thompson Sampling for Machine Learning
R.J. Mak
Greenhouse Group
PyData Amsterdam 2018
May, 26, 2018

2. Introduction
Group of online marketing
agencies, part of GroupM
Tech Hub
Creative Hub
Data Hub
Data Science Team
Data Technologist Team
Data Insights Team
Consumer Experience
Marketing Team

3. Multi-Armed Bandit Problem
How to optimally insert
coins in slot machines when
reward distributions of each
machine are unknown?
Exploitation vs. exploration
tradeoff

4. Applications
Any setting where data
(observations) are costly.
Pretty much any data
science project,
underemphasized.
Deep learning: most focus
on cases where data is
(nearly) abundant.
Classical examples:
Finance
Testing in online
marketing (websites, ads)
Budget allocation R&D
Clinical trials

5. Applications

6. Thompson Sampling: some history
Formulated by Thompson in 1933.
Allied scientists in World War II, proposed to drop the
Multi-armed bandit problem over Germany so that German
scientists could also waste their time on it.
1997 proof of convergence.
Asymptotic convergence results for contextual bandits were
published in 2011.
2012 proven to be optimal for the case of Bernoulli rewards
(Lai and Robbins lower bound for the cumulative regret).

7. Thompson Sampling
Choosing the action that
maximizes the expected
reward with respect to a
randomly drawn belief.
Example of three slot
machines, equal reward,
probability of winning?
Construct reward
distribution. (Beta
distribution).
Sample from those
distributions to choose the
next slot machine.

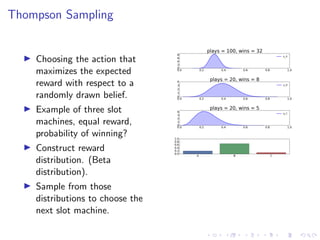
8. Thompson sampling using numpy
1 import numpy as np
2
3 plays = np.array([100, 20, 20])
4 wins = np.array([32, 8, 5])
5 num_samples = 1000000
6
7 p_A_sample = np.random.beta(wins[0], plays[0] - wins[0], num_samples)
8 p_B_sample = np.random.beta(wins[1], plays[1] - wins[1], num_samples)
9 p_C_sample = np.random.beta(wins[2], plays[2] - wins[2], num_samples)
10
11 mab_wins = np.array([0.0, 0.0, 0.0])
12
13 for i in range(num_samples):
14 winner = np.argmax([p_A_sample[i], p_B_sample[i], p_C_sample[i]])
15 mab_wins[winner] += 1
16
17 mab_wins = mab_wins / num_samples
18
19 print(mab_wins)

9. Prediction probabilities vs. prediction distributions
Prediction probabilities and prediction distributions both say
something about uncertainty, what’s the difference?
In the example of object detection, the probabilities are point
estimates of how likely the thing in the picture is a certain
object, for that specific picture. It captures the uncertainty
from the input image.
However, it does not capture the uncertainty from the data
used to train the model. This is what we want to capture with
a prediction distribution.

10. Prediction probabilities vs. prediction distributions

11. Traditional (frequentist) clinical trial
Purely random split test subjects into two groups, group A
gets the treatment, group B gets a placebo.
Often assumption of homogeneous group is made (same effect
for everybody), or, formally, a specific hypothesis needs to be
made at the start of the research about specific heterogeneity.
Medicine often has dangerous side effects for women (and
possibly children, or other minorities).
Time to market of new medicine also plays a role.
Maurits Kaptein (JADS): ”It is unethical to use randomized
controlled trials to personalize health-care”.
{patient, time, treatment, dose}
f
→ outcome

12. Edward
Python package for probabilistic modeling and inference
Build on top of Tensorflow
Bayesian neural networks
Non-Bayesian machine learning: point estimates of
coefficients and predictions
Bayesian: distributions of coefficients and predictions

13. Toy data set
A medicine that causes side
effects at a certain dose.
This maximum dose is
depending on gender and
age, and some individual
random noise.
However, the (test subjects)
population is mostly elderly
male.

14. Edward in action
Two-layer Bayesian neural
network.
Set priors uninformative but
at least somewhere near
results.
Posteriors after 1000
iterations.

15. Edward results
Biased for the lowest ages.
Doesn’t capture interaction
effect for lower ages.
Thompson sampling: when
searching max dose, treat
test subjects with doses
sampled from distribution.

16. Frequentist comparison
Frequentists show the effect
more clearly.
Assuming you actually have
the correct model
assumptions.
Posterior draws always
normal distributions, no
option to balance between
including or not including
interaction term.

17. Edward age as integer input
Trying to smooth by taking
age as single integer input
variable.
Bias variance trade-off.
Better at capturing
interaction effects, draws
look nice.
Doesn’t capture uncertainty
for lowest ages.

18. Frequentist vs. Bayesian neural network
Human hypothesis vs.
discovering with machine
learning.
Simple and specific input
variables (age and gender)
vs. many more possible
input variables (e.g. DNA or
smart sensor data)?
Problems with current
scientific incentives of
publication and going to
market in pharmaceutics.

19. Data volume: data from practice
The biggest problem is acquiring sufficient data to find
specific relationships, interactions and effects.
What if every treatment could be used as a data point?
Remove the strict boundary between research and application.
Thompson sampling in daily use:
Continuously update distributions with data from practice.
Sample optimal treatment from distributions.

20. Practical and ethical challenges
Practical challenges.
Would you want to be treated according to a randomly
sampled belief or the most likely belief?
Would you always want to be in an experiment?
However, current system is unfair because:
Unfair towards effects and side effects for minorities, because
you need to wait until somebody comes with a hypothesis and
start researching.
Longer time for a medicine to go to market, unfair for patients
that cannot get the treatment (yet).

21. Conclusion
Consider the cost of data acquisition as an essential topic for
any data scientist.
Strategic design of data collection, consider Thompson
sampling.
Edward is definitely worth discovering.
There is no such thing as a free lunch!