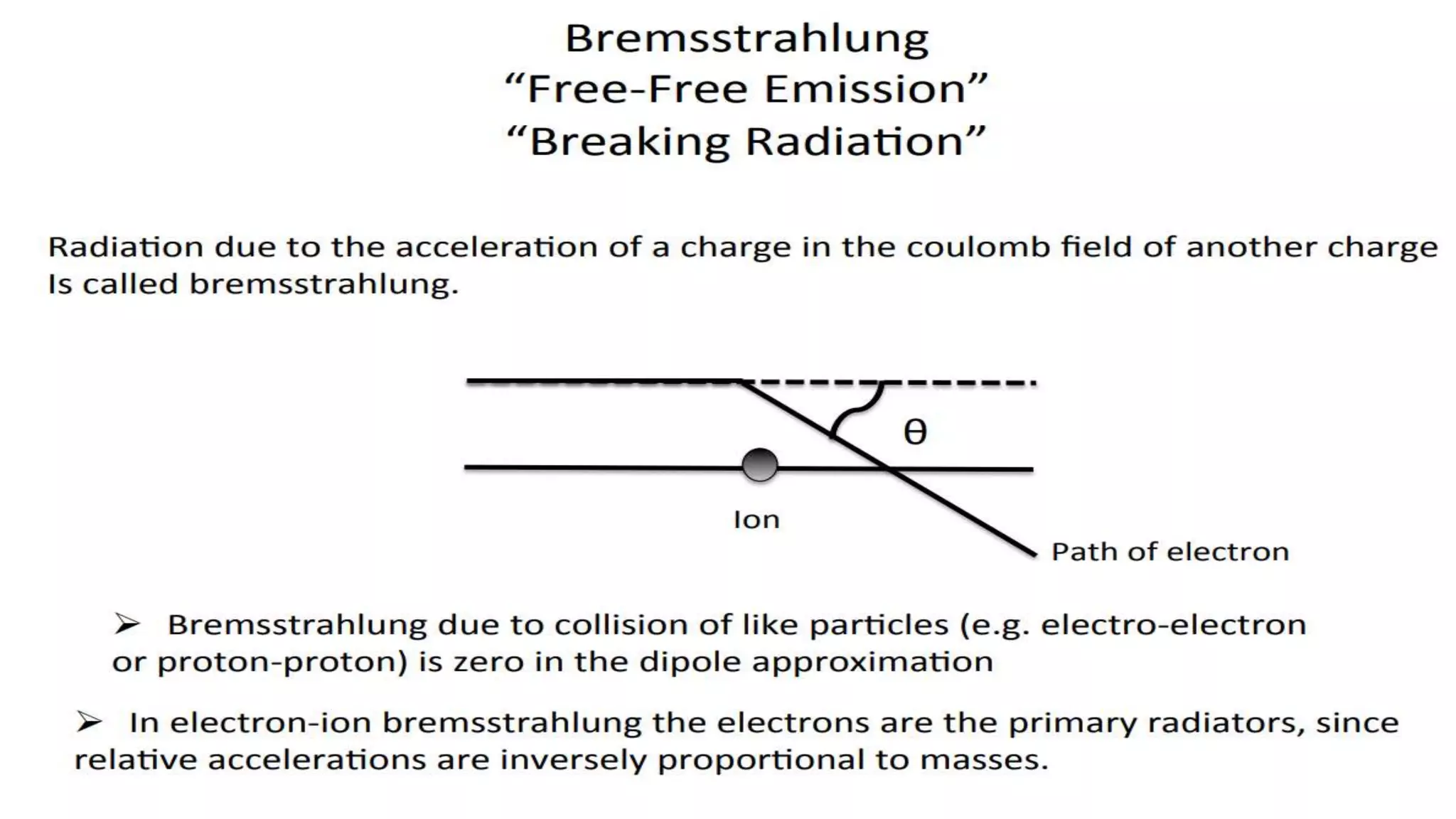
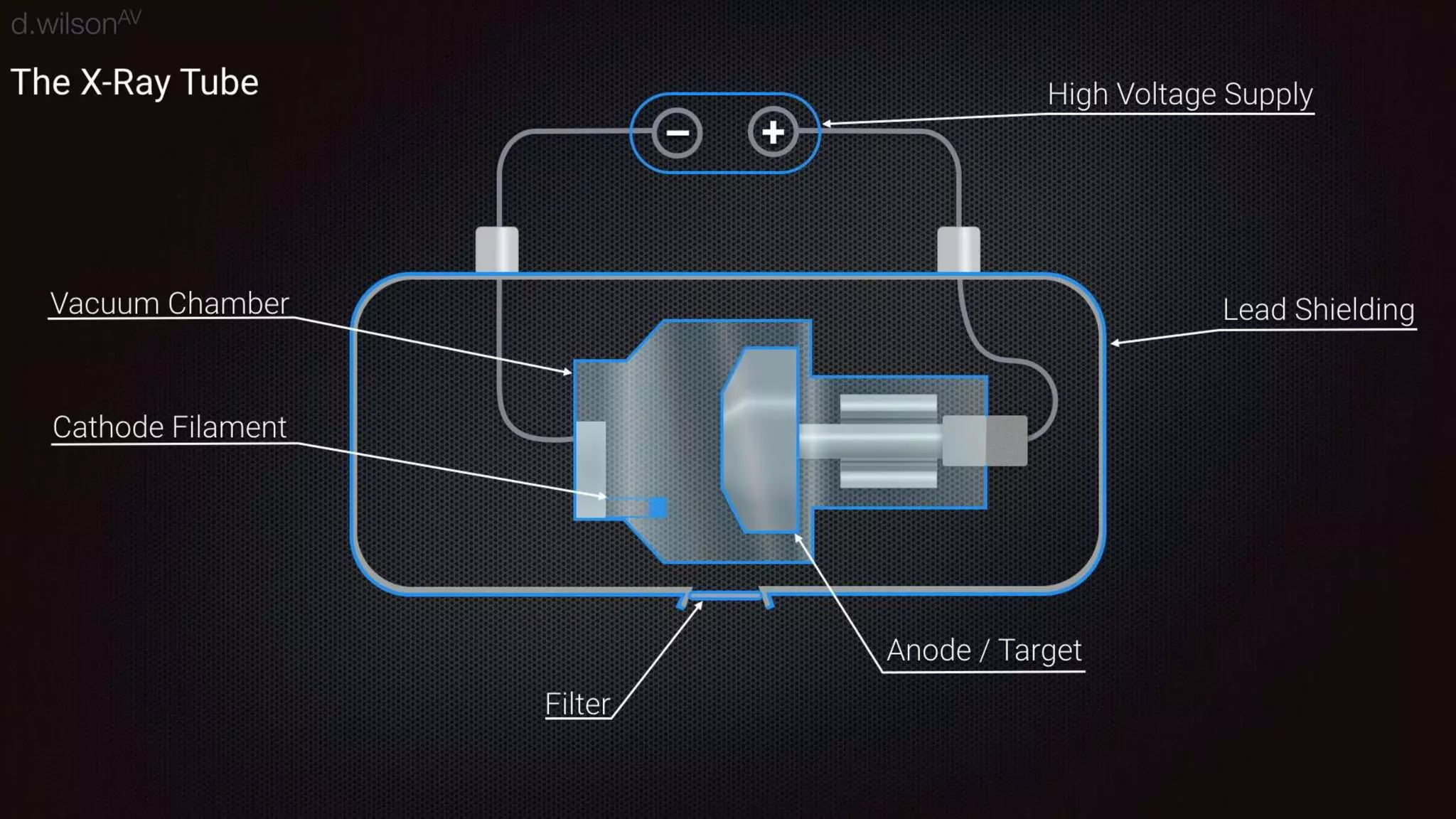
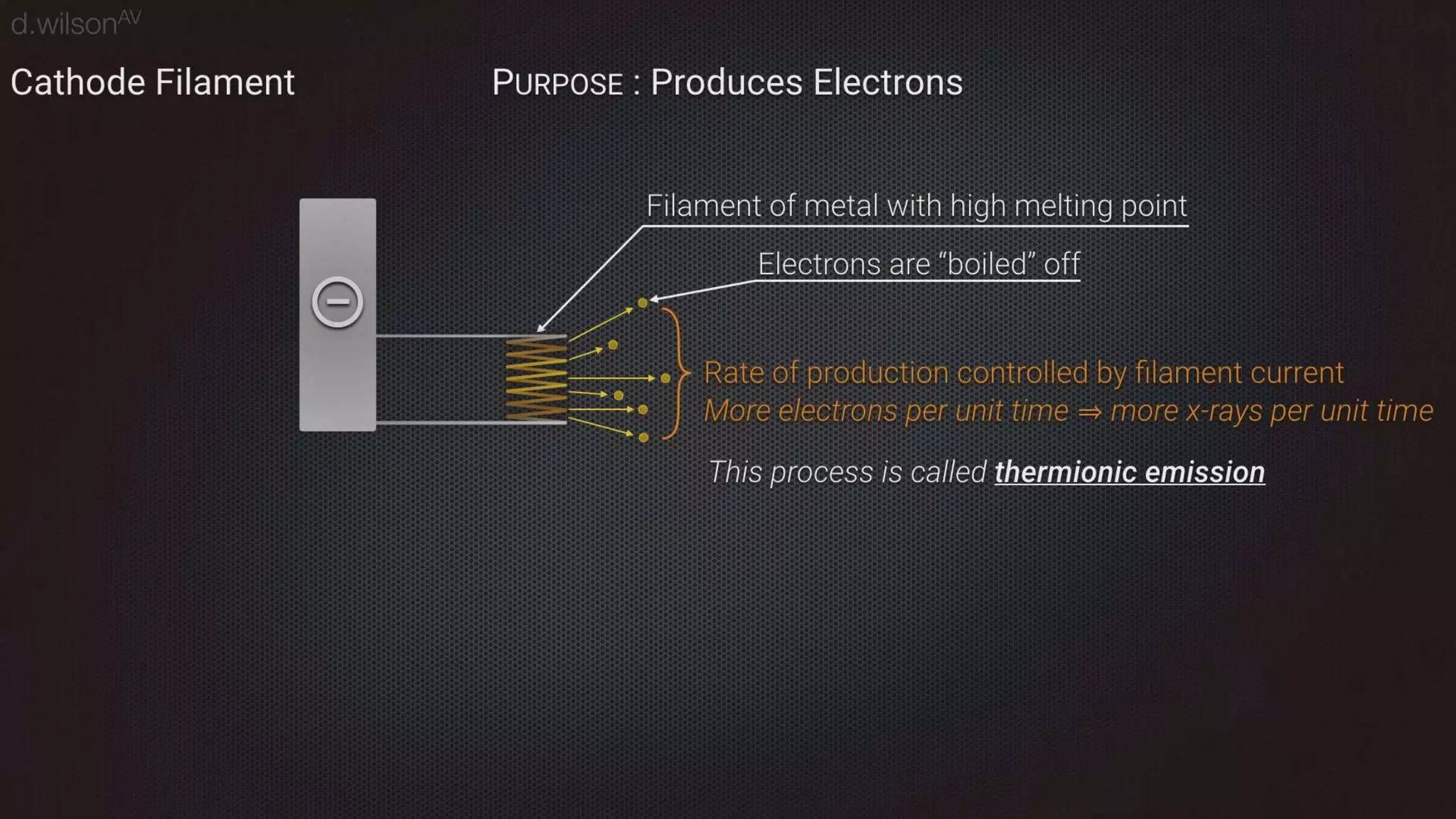
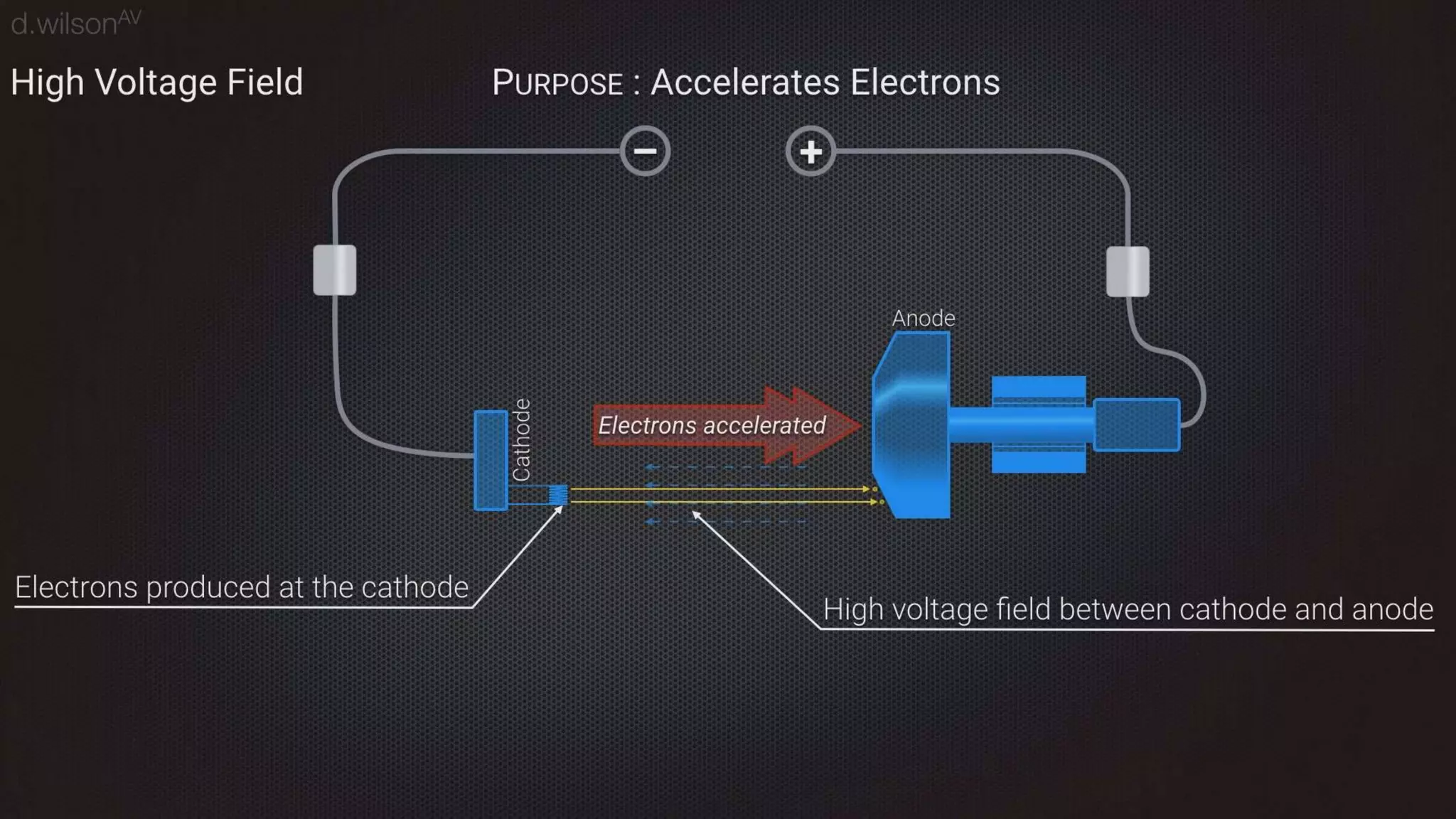
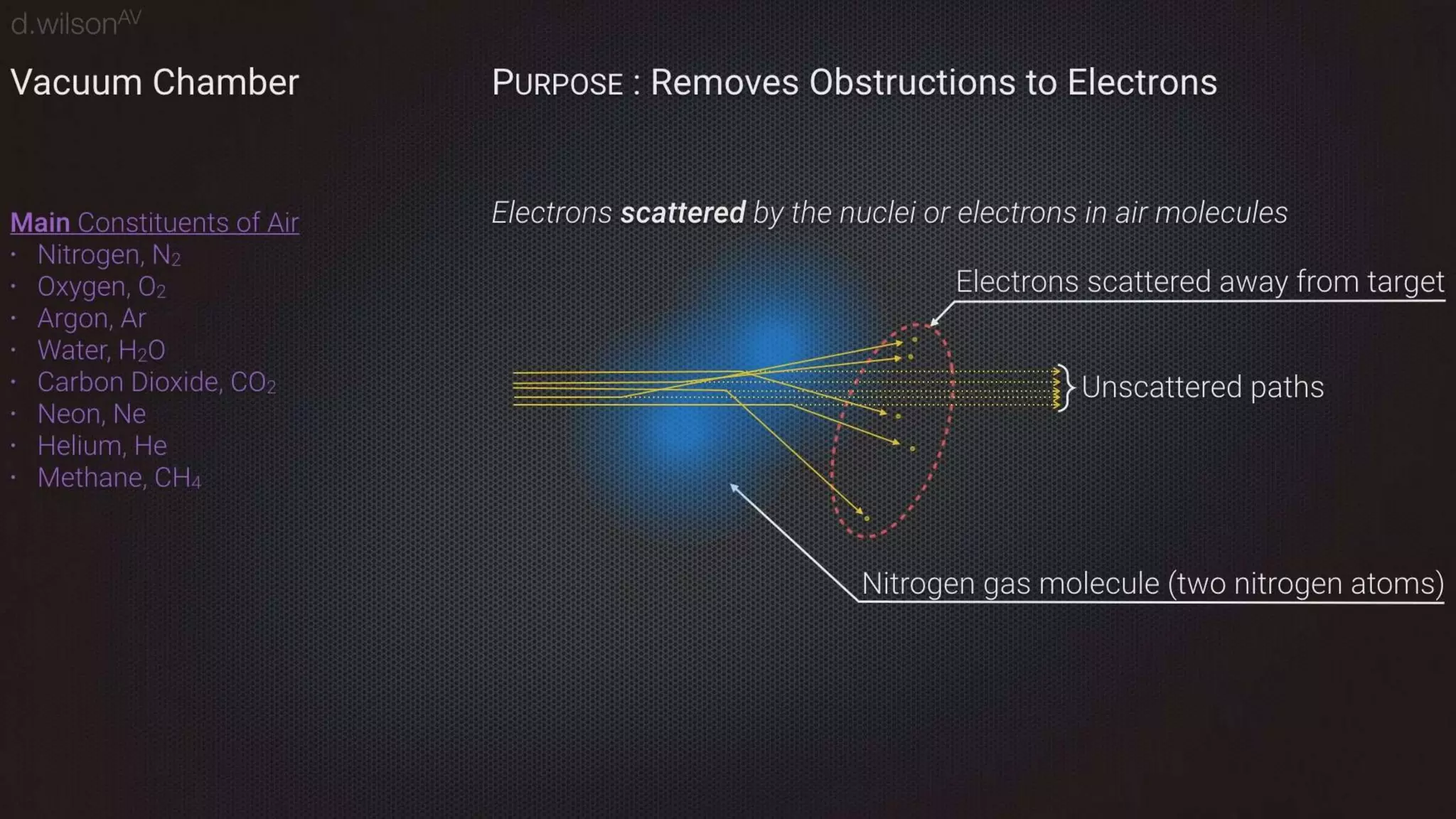
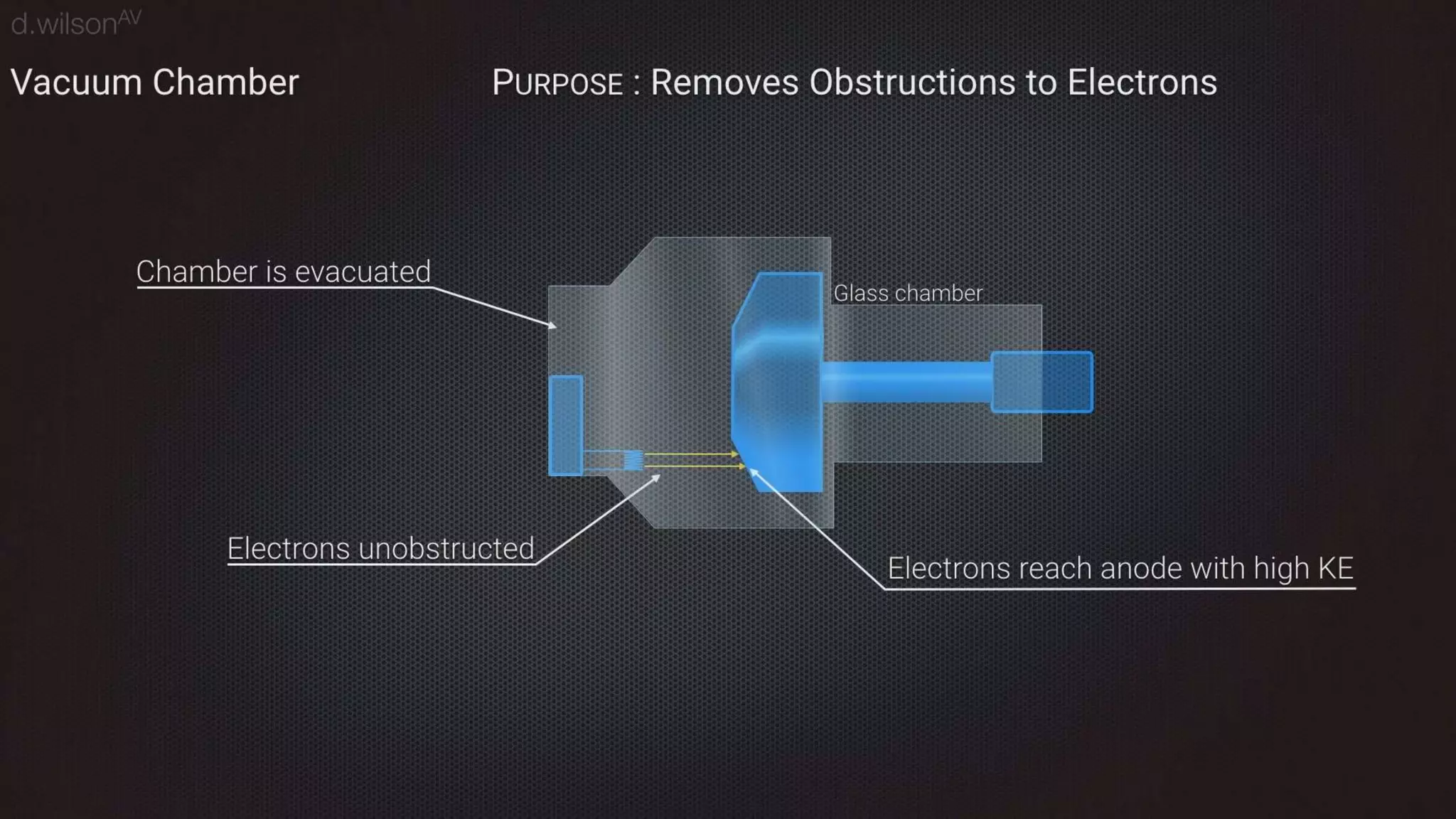
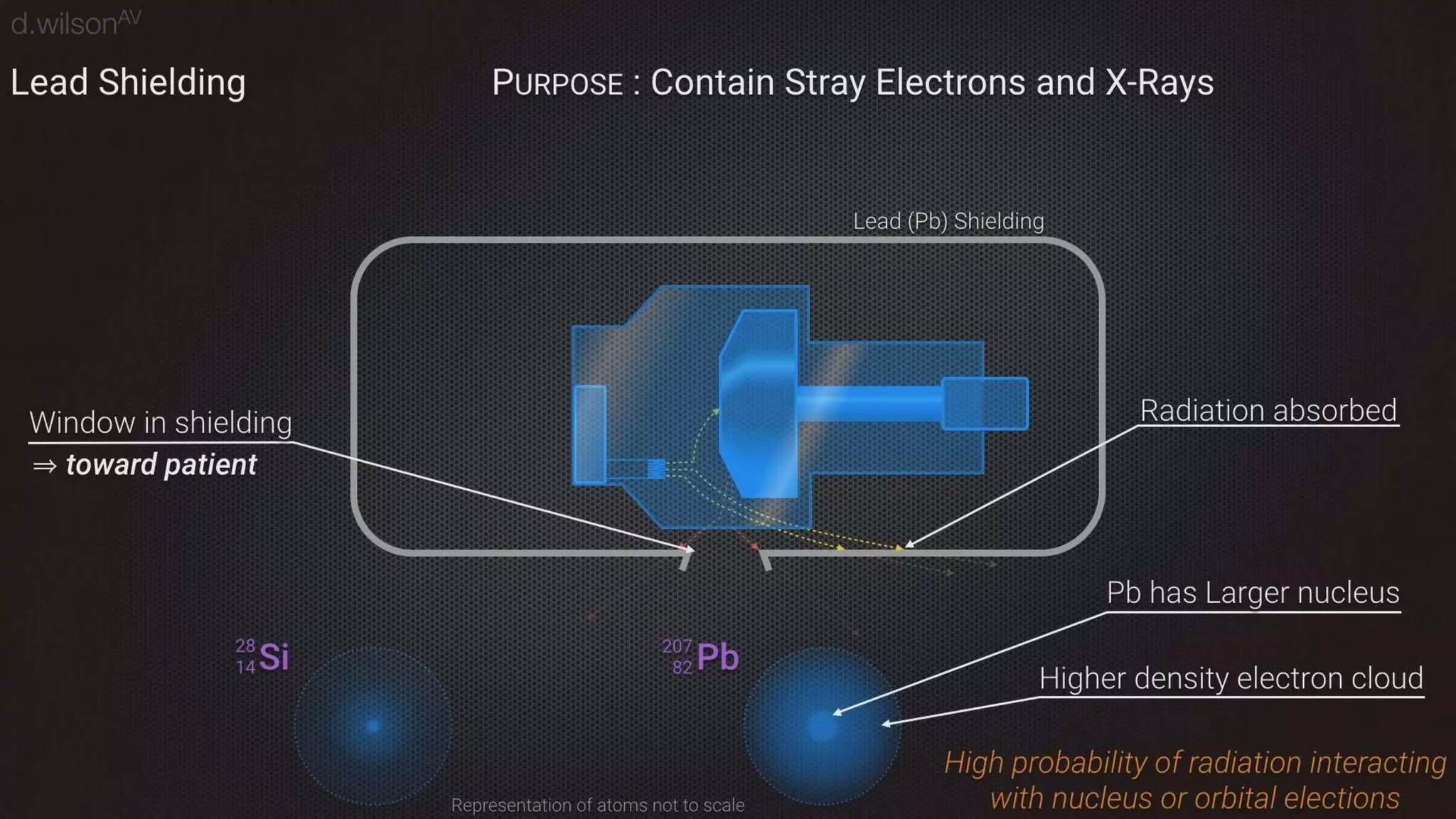
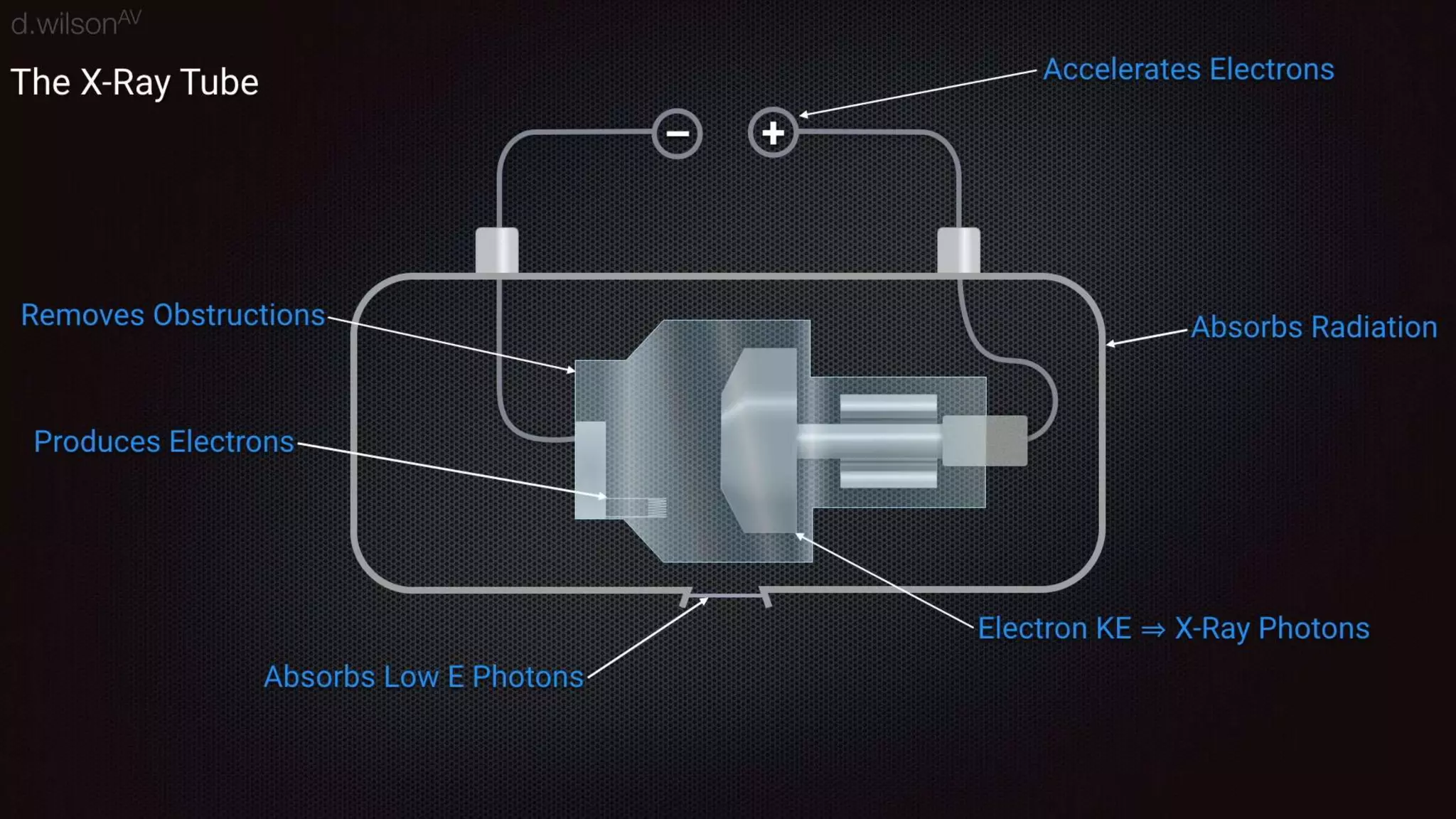
Thermal bremsstrahlung emission and absorption involves the acceleration or deceleration of charged particles in the electric field of another particle or nucleus. Specifically, the document discusses bremsstrahlung radiation emitted when electrons are accelerated or decelerated in the Coulomb field of ions or nuclei, and how this radiation can also be absorbed by charged particles. A classical treatment provides the correct functional dependence for many parameters, though a full quantum understanding is needed since photons with energies comparable to the emitting particle can be produced.

1. THERMAL BREMSSTRAHLUNG
EMISSION AND ABSORPTION

2. Contents
 INTRODUCTION
 EMISSION OF BREMSSTRAHLUNG
RADIATION
 ABSORPTION OF BREMSSTRAHLUNG
RADIATION

3. Thermal Bremsstrahlung

4. ''Radiation due to the acceleration of a charge in the Coulomb field
of another charge is called bremsstrahlung or freefree emission.
A full understanding of the process requires a quantum treatment,
since photons of energies comparable to that of the emitting
particle can be produced,
However, a classical treatment is justified in some regimes, and the
formulas so obtained have the correct functional dependence for
most of the physical parameters.
Therefore, we first give a classical treatment and then state the
quantum results as corrections (Gaunt factors) to the classical
formulas''