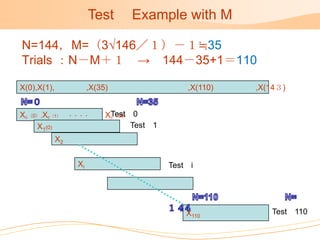
Test(S) is a method proposed by Okabe-Nakano to test if a time series is a realization of a local and weakly stationary process. It evaluates three test values (M) for mean, (V) for variance, and (O) for covariance on subsets of shifted data. The rate at which each test value is accepted over multiple trials is calculated to determine if the data meets the conditions for a stationary process. When applied to an example using KM2O-Langevin data, Test(S) accepted the mean (M) in 80% of trials, variance (V) in 70% of trials, and covariance (O) in 80% of trials.

1. Test（S）
• Test(S)
– Test(S) proposed by Okabe-Nakano [26]
• To test whether a given time series is a realization
of a local and weakly stationary process or not.
– A Criterion that multi-dimensional data are a
realization of a local and weakly stationary
process.
0

2. Test（S）: Z(m） μZ RZ
• Time Series Data Z(m）
– Sample mean vector μZ ,
– Sample covariance matrix function RZ
1

3. Test（S） X(n)

4. Test（S） KM2O-Langevin data
• Sample KM2O-Langevin data
– X: random force of data X
– ξ： one-dimensional standardized white noise

5. Test(S) Conditions
• Three Test Values (M) (V) (O)
(M) mean
(V) variance
(O) Co-variance
• Conditions
4

6. Test(S): Shifted data Xi
sample random force of data Xi
Effective number of the sample covariance matrix function Rx
5

7. Test Example with M
N=144，M=（3√146／１）－１≒35
Trials ：N－M＋１ → 144－35+1＝110
Χ(0),X(1), ,X(35) ,X(110) ,X(14３)
Χ0（0）,Χ0（1） ・・・・ Χ0（35） 0
Test
Χ1(0) Test 1
Χ2
Χi Test i
Χ110 Test 110

8. Test(S)
• Test(S) : The Rate of (M) i （V) i and (O)i which
Test(S) is accepted.
Total Passed ／ Trials (N－M＋１)
• (M) i 80%
• （V) i 70%
• (O) i 80%
7

9. 8