This document provides an introduction to the Haskell programming language. It discusses Haskell's features such as being purely functional, lazily evaluated, statically typed, and supporting currying. It also covers Haskell concepts like functions as first-class citizens, pattern matching, monads, and how Haskell avoids side effects through referential transparency and purity. Examples are given for many of these features to illustrate how they work.

1. Globalcode – Open4education
Trilha – Programação Funcional
Roberto Pepato Mellado
Engenheiro de Software

2. Globalcode – Open4education
Haskell 101

3. “Haskell is a computer programming language. In particular, it is
a p o l y m o r p h i c a l l y s t a t i c a l l y t y p e d , l a z y, p u r e l y
functional language, quite different from most other programming
languages.”
https://wiki.haskell.org/Introduction
Function Application Immutability Currying
Category Theory Monads
Function Composition
…

4. Globalcode – Open4education

5. Understandability
Formalism

6. Data? Code?
int x = 2;
private int incr (int seed)
{
return seed + 1;
}
Code + Data
Prelude> x = 2
Prelude> incr x = x + 1
Code is Data
Functions as first class citizens

7. Static Typing
Prelude> x = 2
-- :type or :t
Prelude> :t x
x :: Num t => t
Prelude> incr x = x + 1
Prelude> :t incr
incr :: Num a => a -> a

8. Basic Types
Type
A collection of related values
Bool
Logical values: True, False.
Char
Single Characters
String
Strings of characters
Int
Fixed-point precision integers
Integer
Arbitrary precision integers
Float
Single-precision floating points
List
Sequence of elements of the same
type
Tuple
A finite sequence of components of
possibly different types
e.g. (Bool -> Bool)
All Bool to Bool function mappings

9. Function Application
In mathematics…
f (a, b) + c d
Prelude> adder a = a + 1
Prelude> tripler c = c * 3
Prelude> adder 2
3
Prelude> adder (tripler 4)
13
f a b + c * d
((f a) b) + c * d

10. Currying
Prelude> sum a b = a + b
Prelude> :t sum
sum :: Num a => a -> a -> a
Prelude> square x = x * x
Prelude> :t square
square :: Num a => a -> a
In haskell, functions are curried

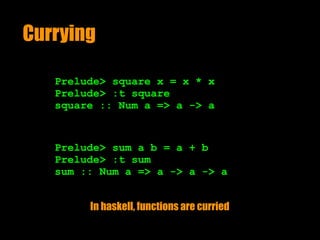
11. Currying
Prelude> :t map
map :: (a -> b) -> [a] -> [b]
Prelude> map (+ 1) [1,2,3,4,5]
[2,3,4,5,6]
Prelude> squares = map square
:t squares
squares :: Num b => [b] -> [b]
squares [1,2,3,4,5]
[1,4,9,16,25]

12. High Order Functions
Prelude> twice f x = f (f x)
Prelude> twice (*2) 3
12
Prelude> twice reverse [1,2,3]
[1,2,3]
Sum of the squares of all even numbers from 1 to 100?
sum: adds items from a list
square: already defined
filter: filter list elements
even: true if a number is even, false otherwise
Prelude> sumsqreven ns = sum(map (square)
(filter even ns))
Prelude> sumsqreven [1..100]
171700

13. Function Composition
Prelude> double x = x + x
Prelude> triple x = double x + x
Prelude> sixTimes = double . triple
Prelude> sixTimes 5
30

14. Function Composition
Prelude> fsum = sum . map (square) . filter even
Prelude> [1..100]
[1,2,3,4,5,6,7,…]
Prelude> fsum [1..100]
171700
Prelude> verifyStatus = …
Prelude> checkCredit = …
Prelude> validate = …
Prelude> generateOrder = …
Prelude> sendEmail = …
Prelude> applyTransaction = sendEmail . generateOrder
. validate . checkCredit . verifyStatus

15. Pattern Matching
Prelude> head [1..10]
1
Prelude> tail [1..10]
[2,3,4,5,6,7,8,9,10]
Prelude> length [] = 0
Prelude> length (_:xs) = 1 + length xs
Prelude> length []
0
Prelude> length [2,2,2,2,2,2,2]
7
Prelude> cabeca (x:xs) = x
1
Prelude> cauda(x:xs) = xs
[2,3,4,5,6,7,8,9,10]
Prelude> cabeca (x:_) = x
Prelude> cauda(_:xs) = xs

16. Pattern Matching
Prelude> check (403, ip, timestamp) = ip
Prelude> check (_, _, _) = “ok”
Prelude> analyzelog xs = [check x | x <- xs]
Prelude> analyzelog [
(200, “200.251.192.13”, 1467313969905),
(403, “200.168.175.28”, 1467314005735),
(500, “201.52.164.78, 1467314029977)
]
“ok”
“200.168.175.28”
“ok”

17. Lazy
Prelude> mult (x, y) = x * y
Call by value
> mult (1+2, 3+4)
{ applying + }
mult (3, 3 + 4)
{ applying + }
mult (3, 7)
{ applying mult }
3 * 7
{ applying * }
21
Call by name
> mult (1+2, 3+4)
{ applying mult }
(1+2) * (3+4)
{ applying + }
3 * (3 + 4)
{ applying + }
3 * 7
{ applying * }
21
Haskell strategy is based
on call-by-name

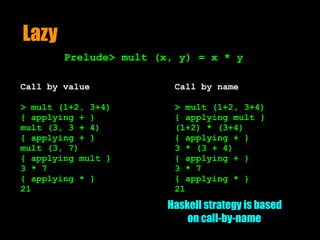
18. Lazy
Prelude> list = 1 : 2 : []
[1,2]
Call by value
> head ones
{ applying ones }
head (1 : ones)
{ applying ones }
head (1 : (1 : ones))
{ applying ones }
.
.
.
> ones = 1 : ones
> ones
{ applying ones }
1 : ones
{ applying ones }
1 : (1 : ones )
{ applying ones }
1 : (1 : (1 : ones))
[1, 1, 1, 1, 1, 1, 1, 1, 1…]

19. Lazy
Prelude> list = 1 : 2 : []
> ones = 1 : ones
> ones
{ applying ones }
1 : ones
{ applying ones }
1 : (1 : ones )
{ applying ones }
1 : (1 : (1 : ones))
[1, 1, 1, 1, 1, 1, 1, 1, 1…]
Call by name
> head ones
{ applying ones }
head (1 : ones)
{ applying head }
1

20. Immutability
> combine a b = a ++ b
> combine [1,2,3] [4]
[1,2,3,4]
> let x = [1,2,3]
> combine x [4]
[1,2,3,4]
> x
[1,2,3]
> drop 1 x
[2,3]
> x
[1,2,3]

21. Referential Transparency
> incr a = a + 1
> incr 6
7

22. Breaking Ref Transparency
class OrderCalculator {
Order _order;
public Calculator (Order order){
_order = order;
}
public void applyDiscount() {
_order.total *= 0.90;
}
public void applyDeliveryTax() {
_order.total += 10;
}
public double getTotal() {
return _order.total;
}
}
// set order total
Order o = new Order(100);
OrderCalculator oc = new
OrderCalculator(o);
oc.applyDeliveryTax();
oc.applyDiscount();
oc.getTotal(); //99
o = new Order(100);
oc = new
OrderCalculator(o);
oc.applyDiscount();
oc.applyDeliveryTax();
oc.getTotal(); //100

23. Pure
1. The function always evaluates the same result value given the same
argument value(s). The function result value cannot depend on any hidden
information or state that may change while program execution proceeds or
between different executions of the program, nor can it depend on any external
input from I/O devices.
2. Evaluation of the result does not cause any semantically observable side
effect or output, such as mutation of mutable objects or output to I/O devices.
read
data
write
data
raise
exception
change
state
…

24. Monads
A monad is a way to structure computations in terms of values and
sequences of computations using those values.
It is a parameterized type m that supports return and bind functions of the
specified types.
class Monad m where
return :: a -> ma
(>>=) :: ma -> (a -> mb) -> mb
It allows computation to be isolated from side-effects and non-
determinism.

25. More?
Enjoy this track :)
Programming in Haskell - Graham Hutton
Real World Haskell - http://book.realworldhaskell.org/read/
Learn You a Haskell for Great Good - http://learnyouahaskell.com
A Gentle Introduction to Haskell - https://www.haskell.org/tutorial/
Introduction to Functional Programming - Erik Meijer - edX
Don’t Fear the Monad (search on youtube) - Brian Beckman

26. Globalcode – Open4education
Thanks!
http://www.slideshare.net/rpepato
@rpepato