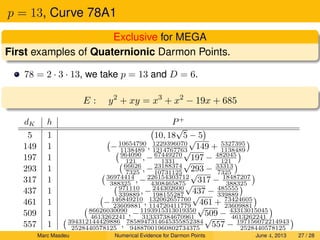
1. The document discusses numerical calculations of Darmon points, which are conjectural algebraic points on elliptic curves defined over real quadratic fields.
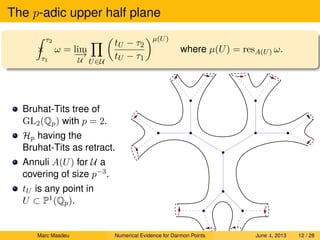
2. Darmon points are constructed using p-adic integration on the upper half-plane and cohomology classes associated to the elliptic curve.
3. Examples of calculating Darmon points are presented for various elliptic curves and real quadratic fields using Sage code implementing the necessary algorithms.











![Darmon points `a la Greenberg
Assumption
1 K is real quadratic.
2 S(K, N) = { : | pD} has odd cardinality.
Write N = pDM, and B/Q = quaternion algebra of discriminant D.
Fix ιp : B → M2(Qp).
B×
→ GL2(Qp) acts on Hp by:
a b
c d τ =
aτ + b
cτ + d
.
R an Eichler order of level M (and such that ιp(R) is “nice”
ιp(R) ⊂ a b
c d ∈ M2(Zp) : vp(c) ≥ 1 .
).
Γ = R[1
p ]
×
1
(elements in R[1
p ] of reduced norm 1) → SL2(Qp).
If D = 1, then B = M2(Q) and Γ = a b
c d ∈ SL2(Z[1/p]) : M | c .
Marc Masdeu Numerical Evidence for Darmon Points June 4, 2013 14 / 28](https://image.slidesharecdn.com/talkmegahandout-140729114509-phpapp02/85/Numerical-Evidence-for-Darmon-Points-14-320.jpg)
![Cohomology
Let Ω1
Hp,Z = rigid-analytic differentials having integral residues.
Can attach to E a unique (up to sign) class [ΦE] ∈ H1 Γ, Ω1
Hp,Z .
Uses Hecke action and Jacquet–Langlands correspondence.
Theorem (M. Greenberg)
There exists a unique class [ΦE] ∈ H1(Γ, Ω1
Hp,Z) satisfying:
1 T [ΦE] = a [ΦE] for all primes pDM;
2 U [ΦE] = a [ΦE] for all | DM;
3 Wp[ΦE] = ap[ΦE] (Atkin-Lehner involution);
4 W∞[ΦE] = [ΦE] (Involution at ∞).
Hecke action can be made explicit
Suitable for computation.
Marc Masdeu Numerical Evidence for Darmon Points June 4, 2013 15 / 28](https://image.slidesharecdn.com/talkmegahandout-140729114509-phpapp02/85/Numerical-Evidence-for-Darmon-Points-15-320.jpg)
![Homology
Start with an embedding ψ: K → B.
ψ induces an action of K× on Hp via ιp.
1 Let τψ ∈ Hp be the unique fixed point of K×
2 Set γψ = ψ( 2
), where O×
K = {±1} × .
ψ ; ˜Θψ = [γψ ⊗τψ] ∈ H1(Γ, Div Hp).
Key exact sequence:
H1(Γ, Div0
Hp) // H1(Γ, Div Hp)
deg
// H1(Γ, Z)
Θψ
? // ˜Θψ
// torsion
Challenge: pull
a multiple of
˜Θψ back to Θψ ∈ H1(Γ, Div0
Hp).
Requires algorithms adapted to the nature of Γ.
Marc Masdeu Numerical Evidence for Darmon Points June 4, 2013 16 / 28](https://image.slidesharecdn.com/talkmegahandout-140729114509-phpapp02/85/Numerical-Evidence-for-Darmon-Points-16-320.jpg)
![Conjecture
Recall our data
1 Θψ = [ γ γ ⊗Dγ] ∈ H1(Γ, Div0
Hp)
2 ΦE ∈ Z1(Γ, Ω1
Hp,Z)
Jψ =
γ
×
Dγ
(ΦE)γ ∈ K×
p .
Jψ is well defined modulo powers of the Tate parameter qE
Conjecture (Darmon (D = 1), Greenberg (D 1))
1 Pψ = ΨTate(Jψ) belongs to E(Kab)
2 If rkan(E, K) = 1, then Pψ has infinite order.
Marc Masdeu Numerical Evidence for Darmon Points June 4, 2013 17 / 28](https://image.slidesharecdn.com/talkmegahandout-140729114509-phpapp02/85/Numerical-Evidence-for-Darmon-Points-17-320.jpg)