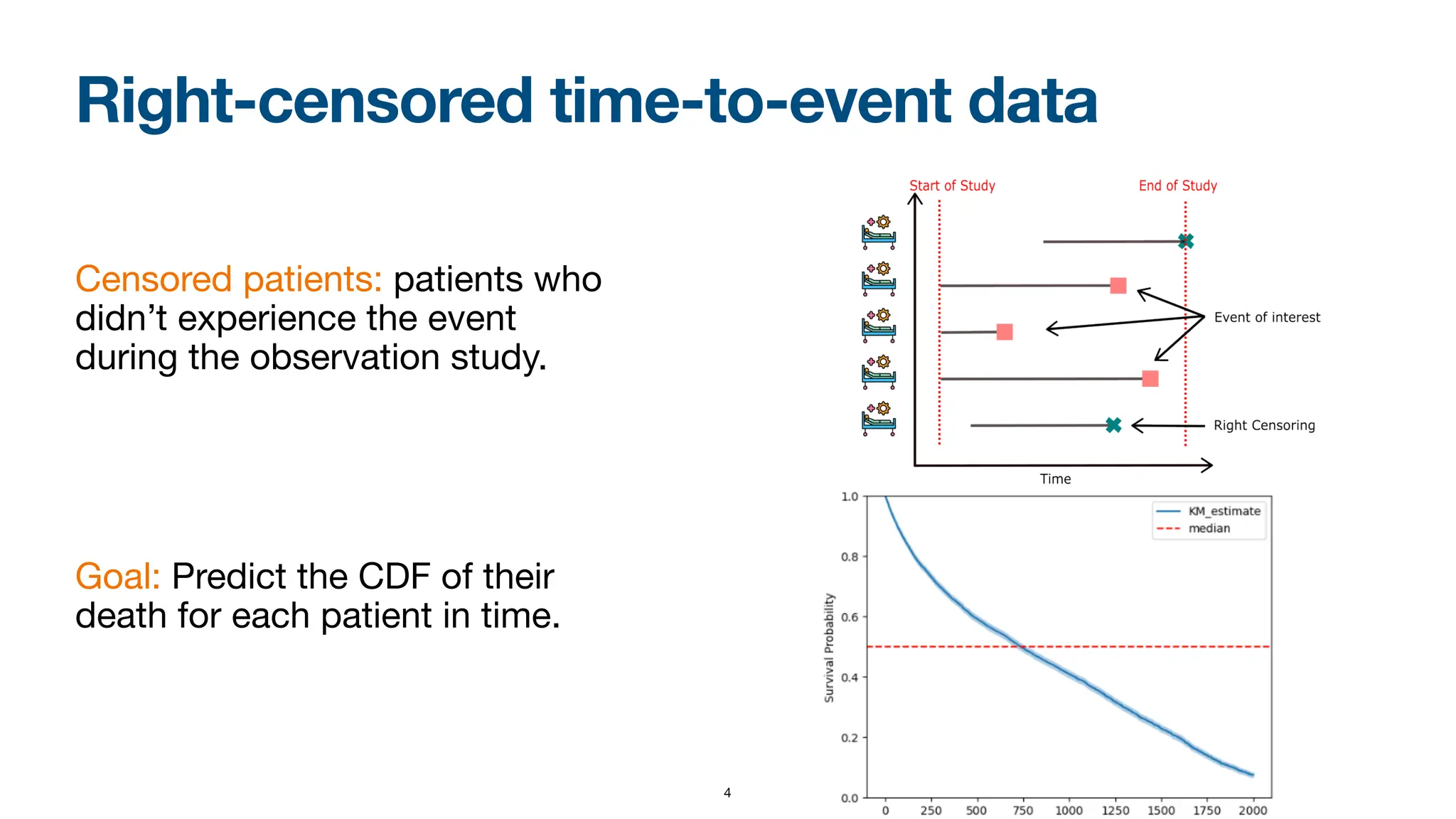
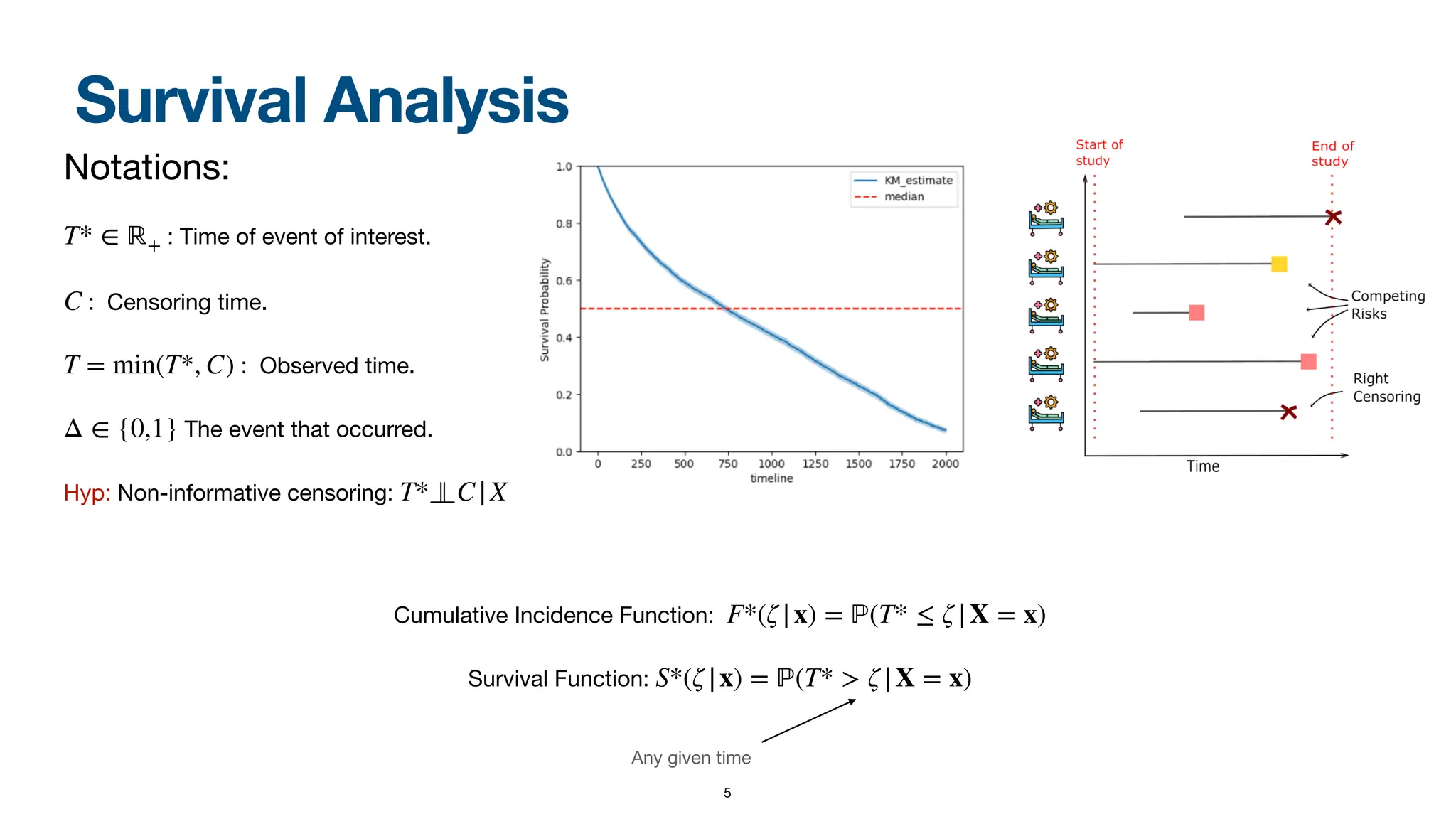
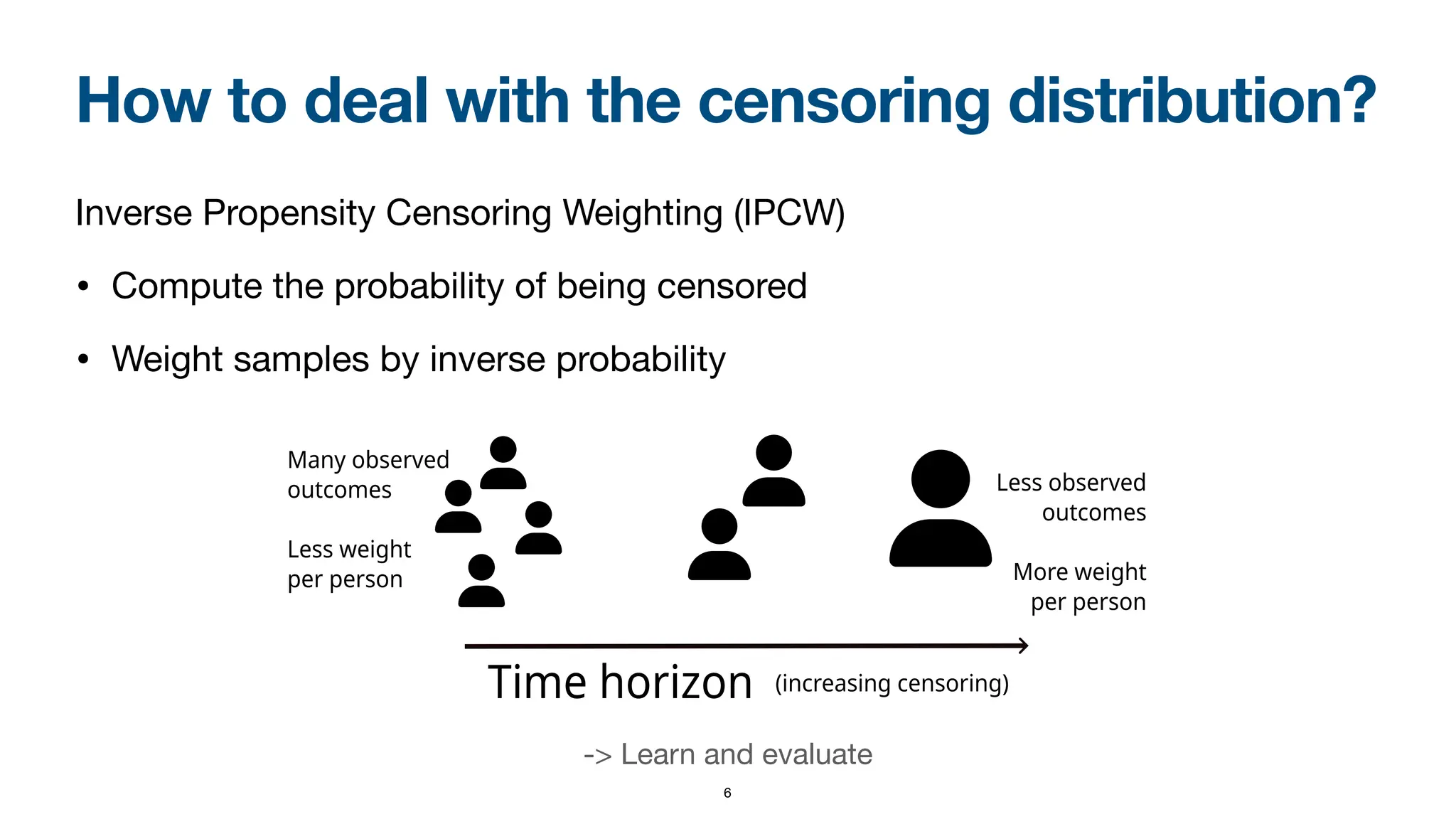
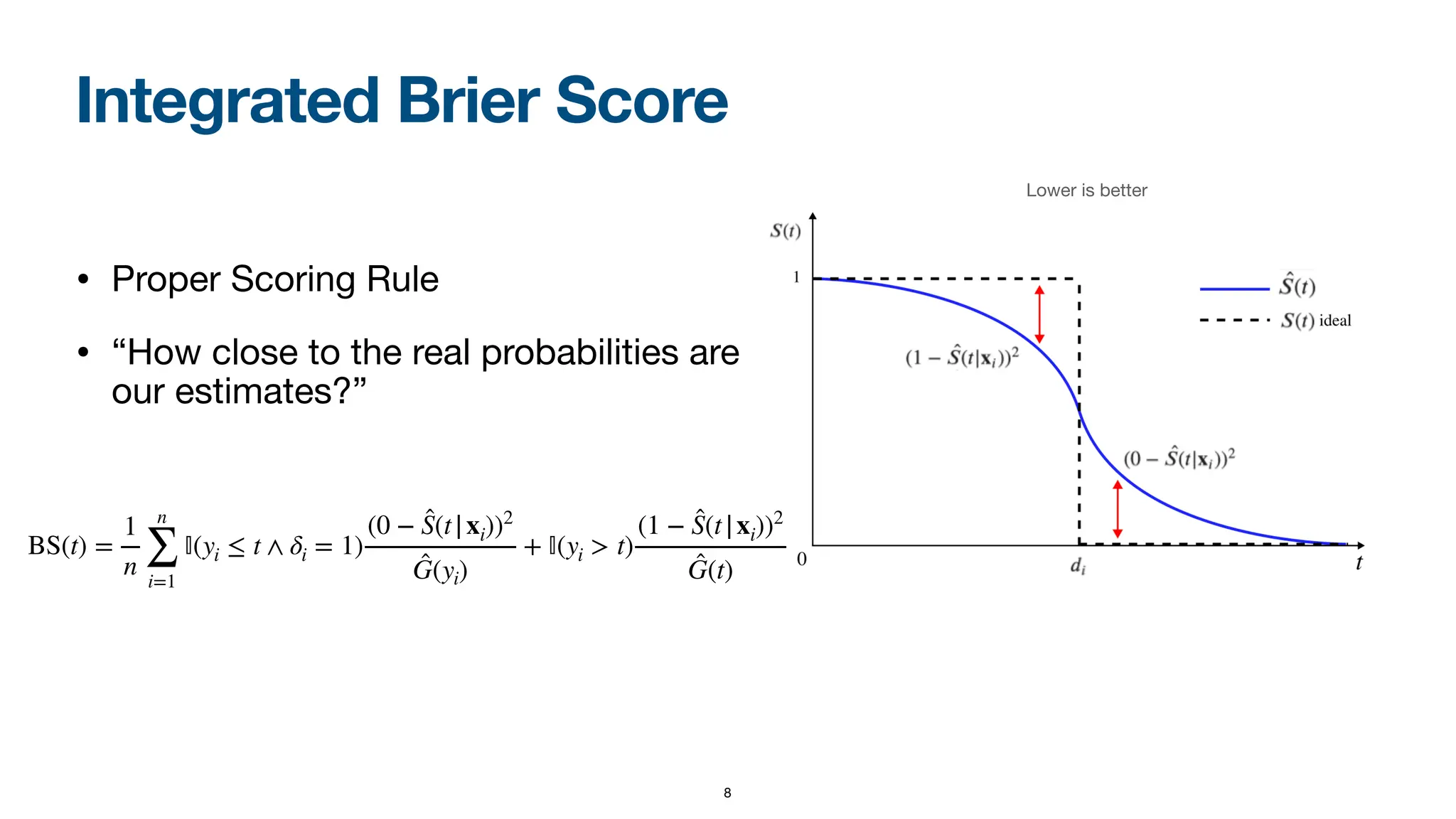
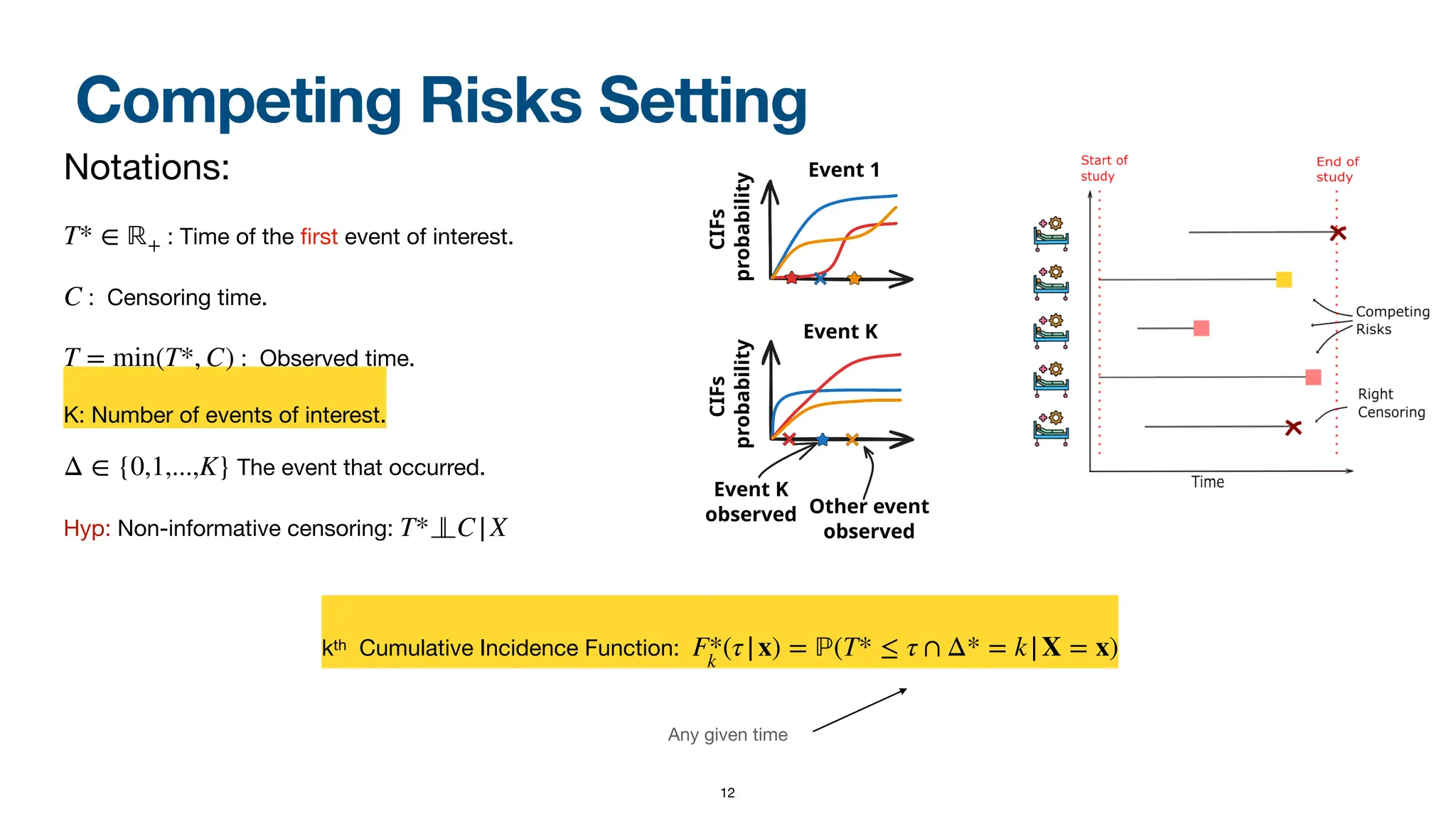
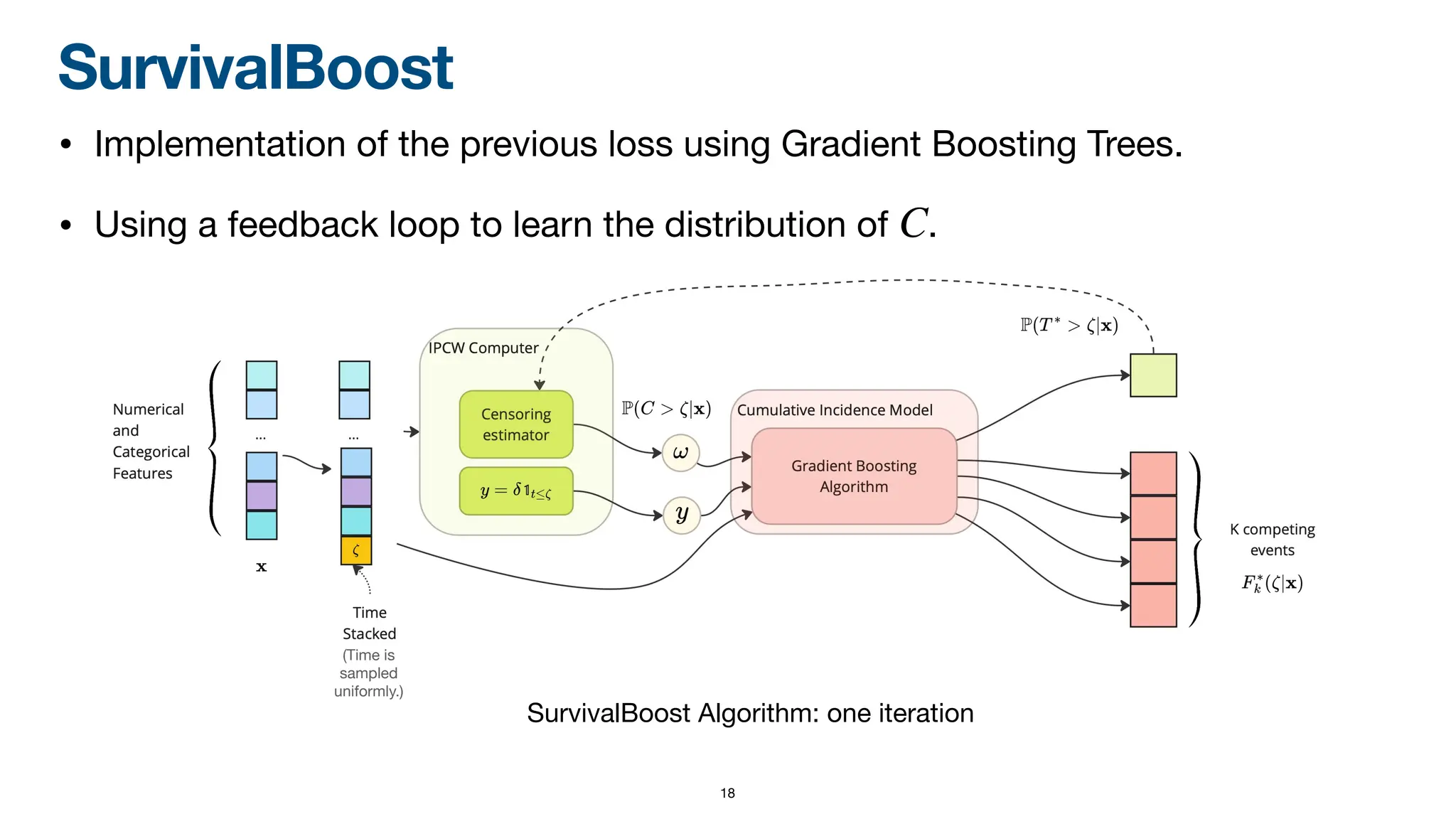
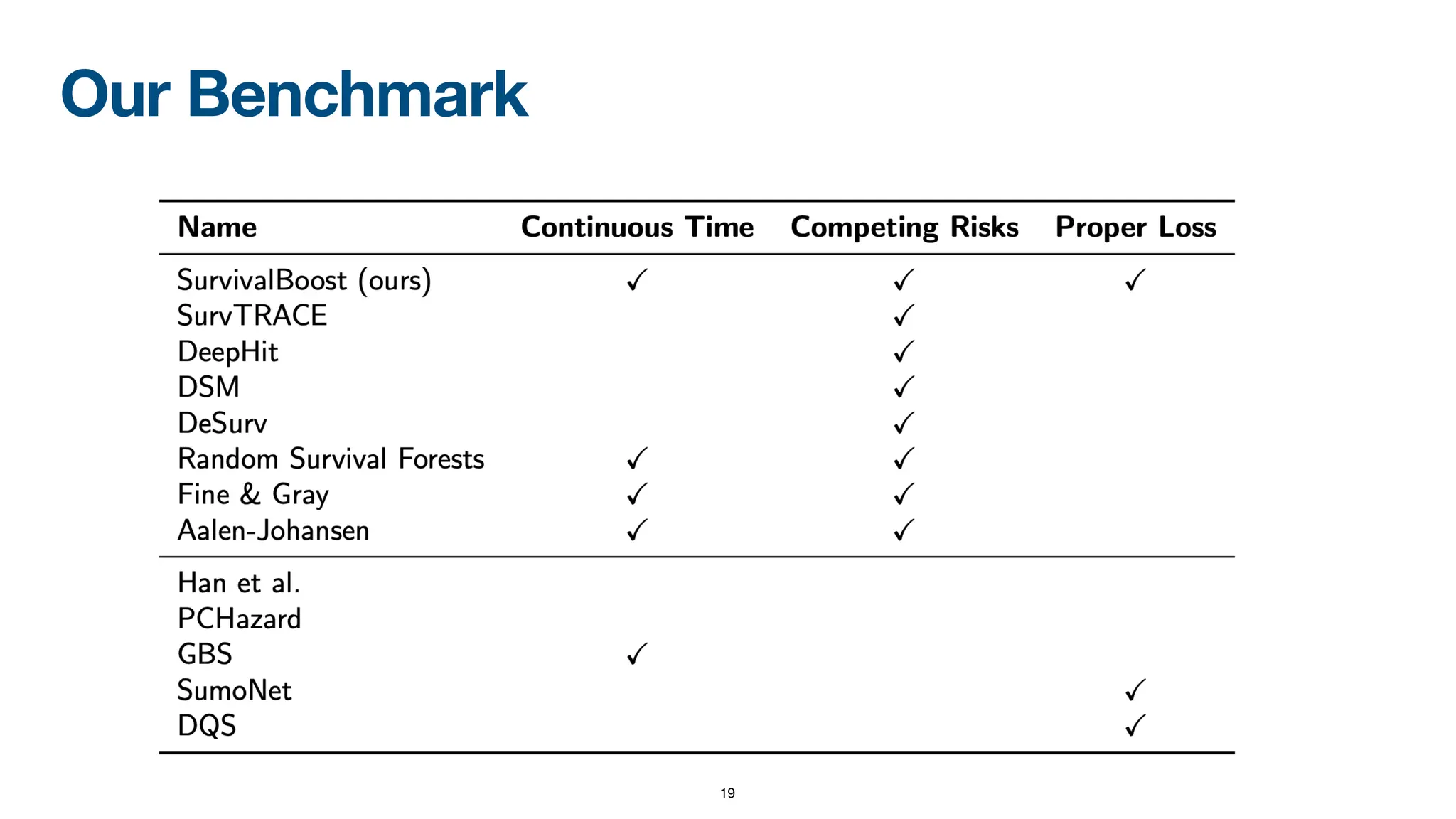
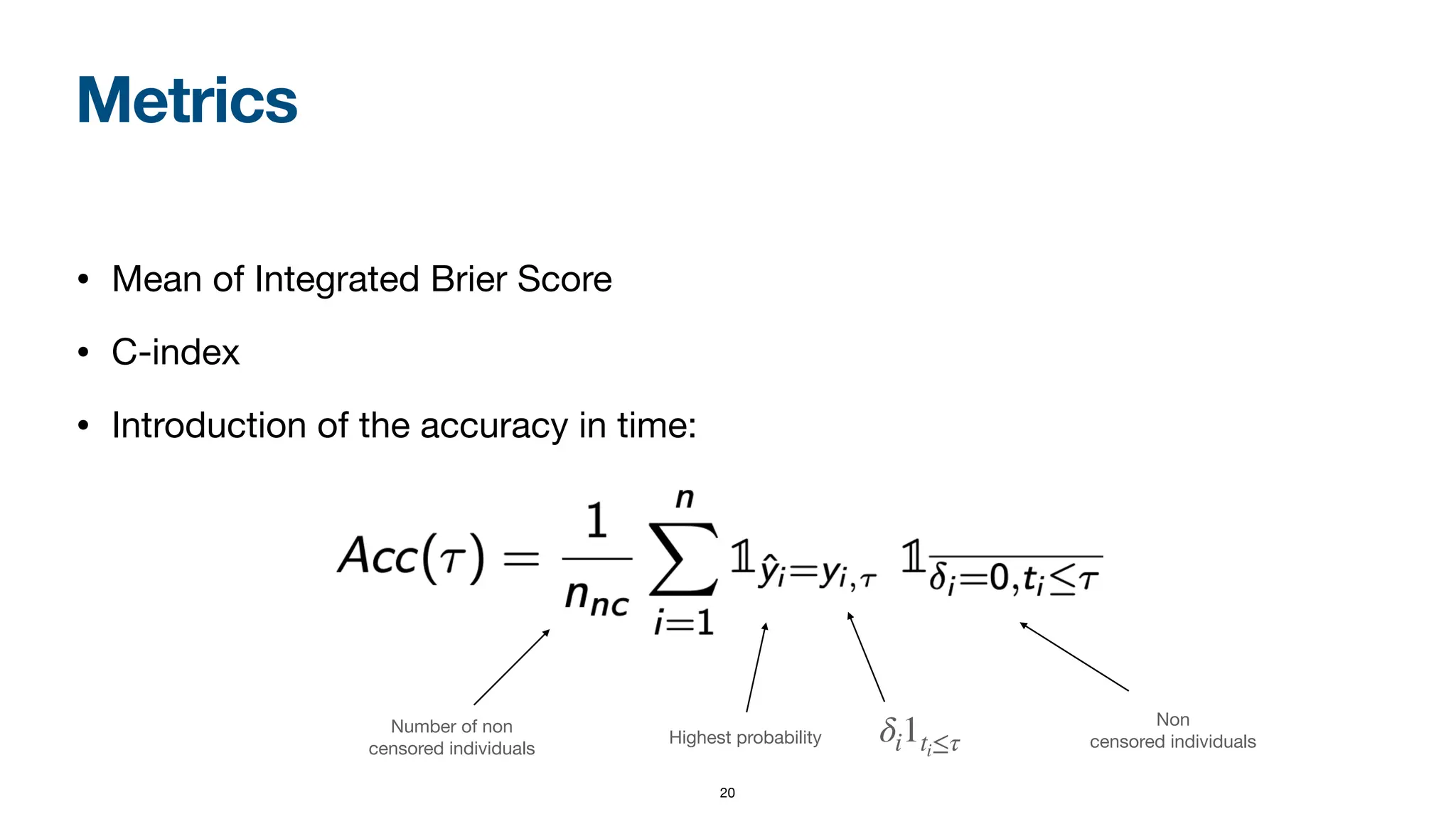
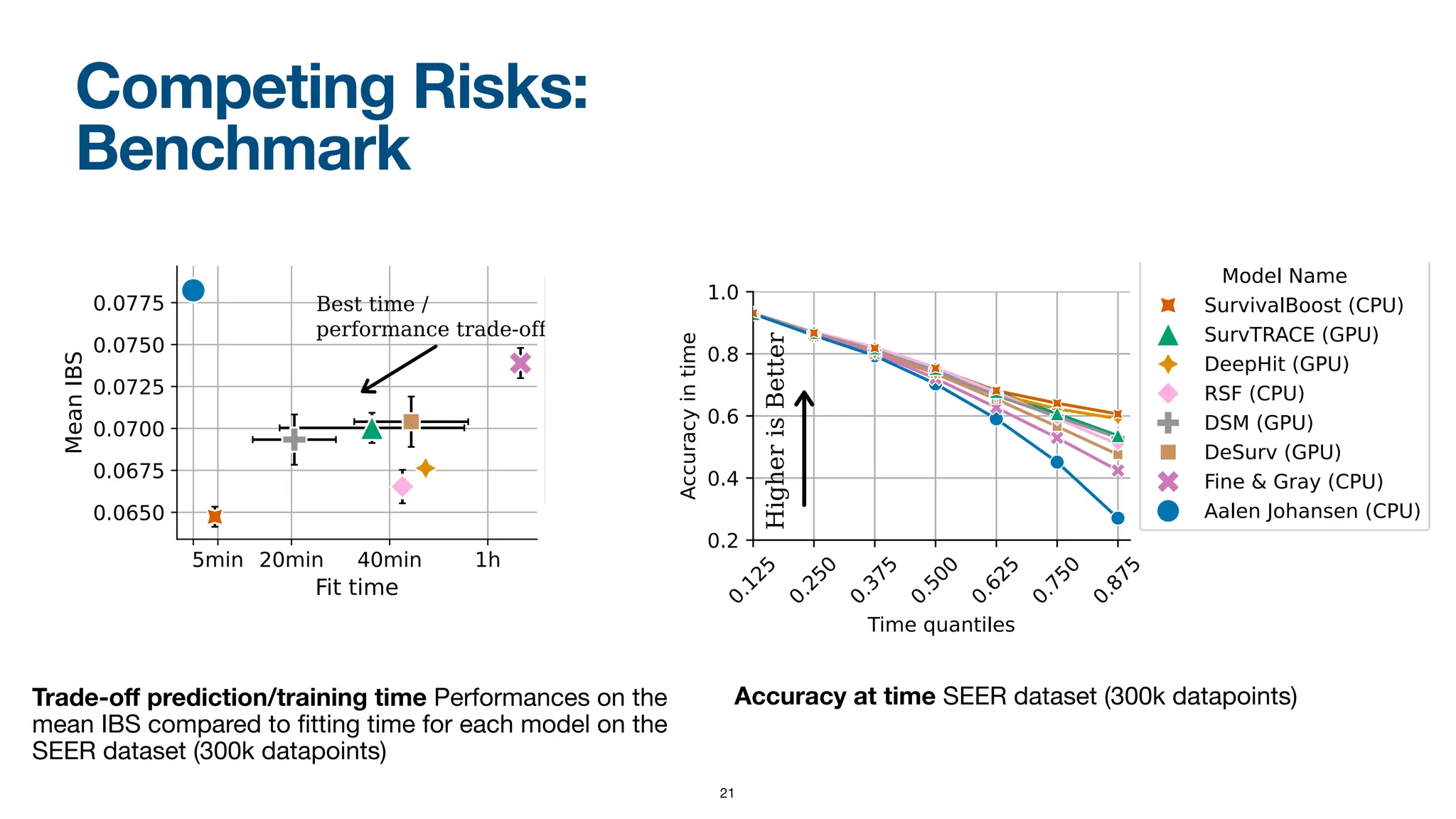
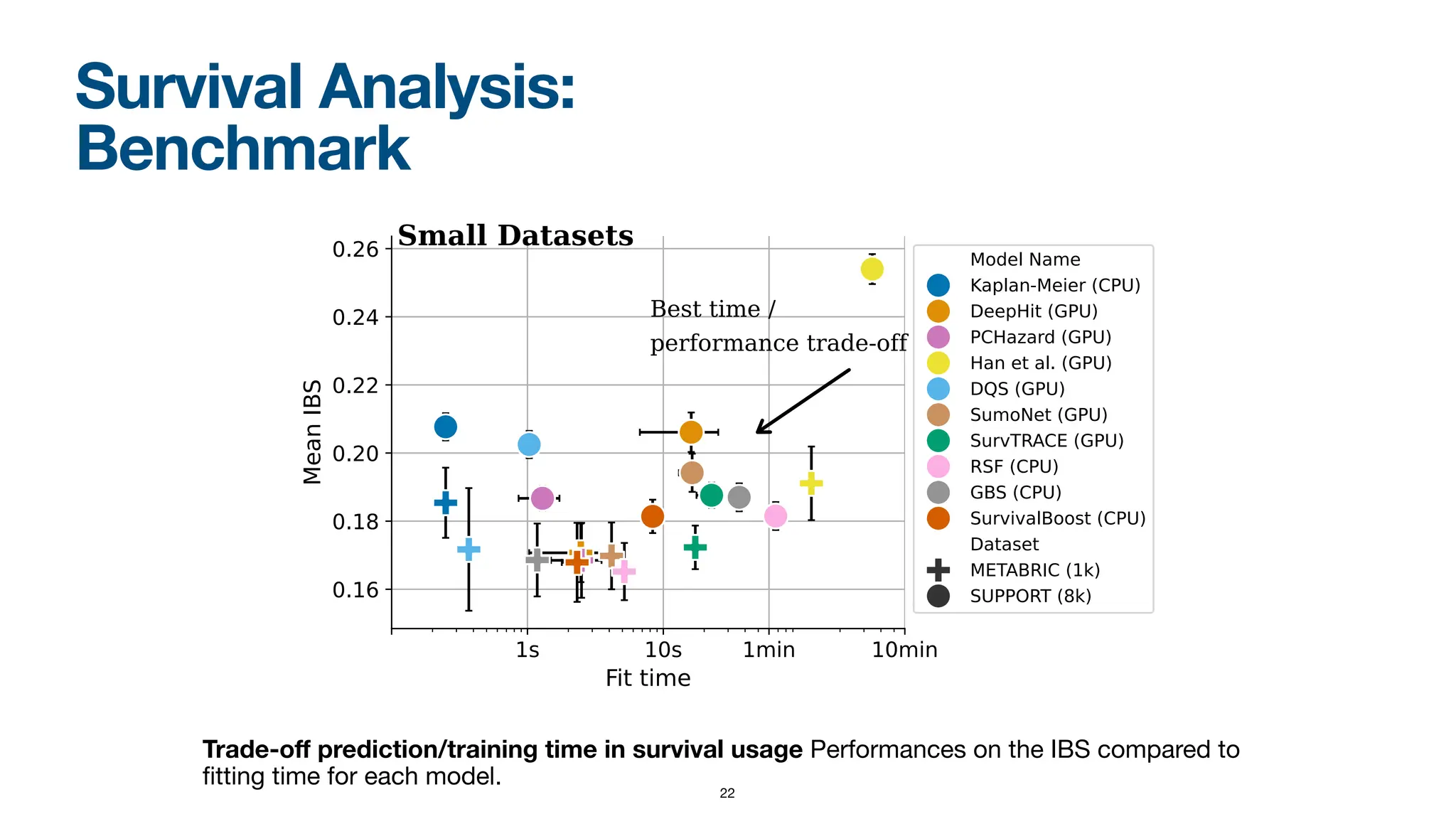
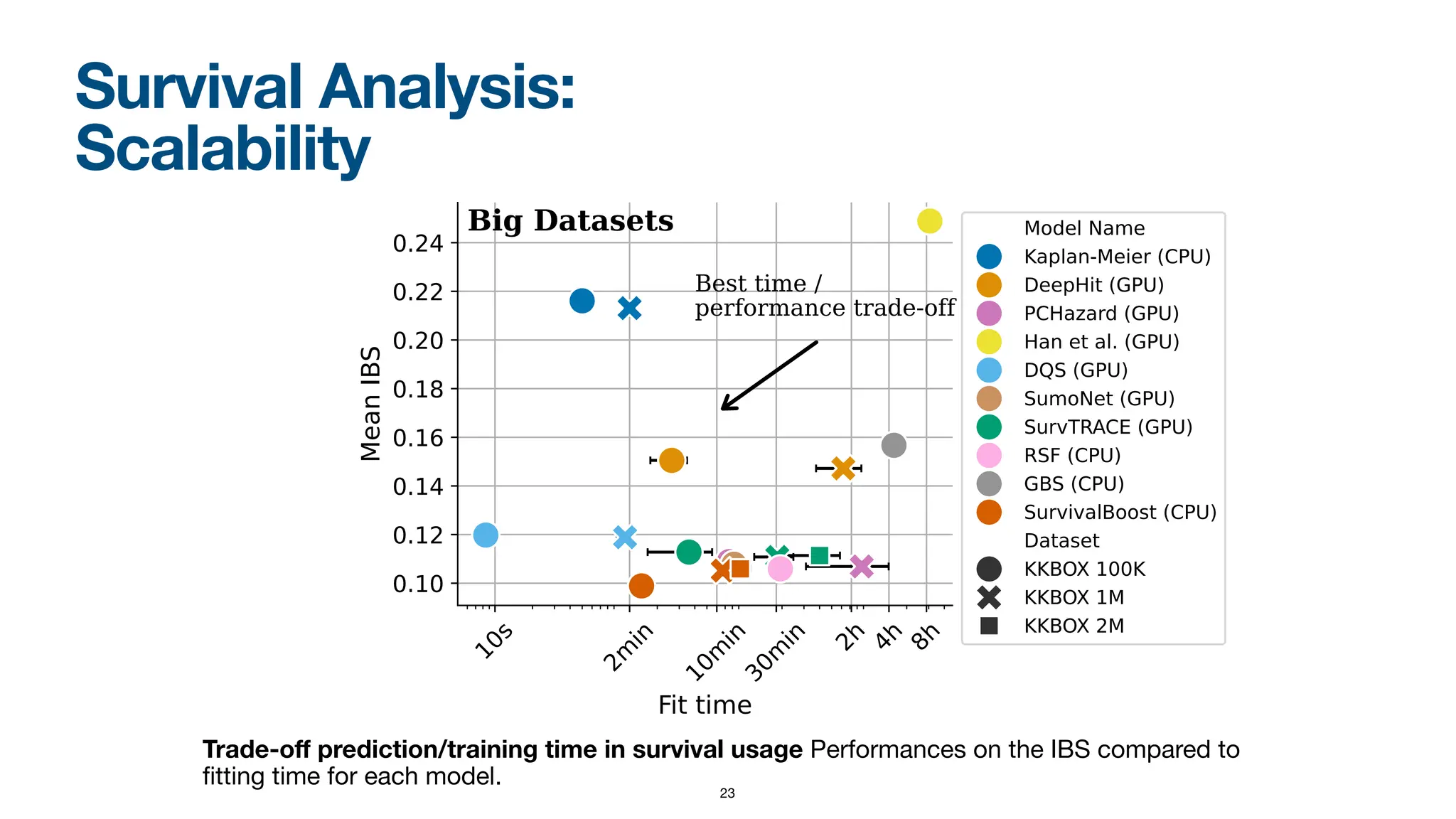
When dealing with right-censored data, where some outcomes are missing due to a limited observation period, survival analysis focuses on predicting the time until an event of interest occurs. Multiple classes of outcomes lead to a classification variant: predicting the most likely event, an area known as competing risks.

1. 12/06/2025
Survival Models:
Proper Scoring Rule and Stochastic
Optimization for Competing Risks
Julie Alberge
PhD student under the supervision of Judith Abécassis and Gaël
Varoquaux
1

2. Collaborators
Vincent Maladière Olivier Grisel Judith Abécassis Gaël Varoquaux
2

3. What is survival analysis?
3

4. Right-censored time-to-event data
Censored patients: patients who
didn’t experience the event
during the observation study.
Goal: Predict the CDF of their
death for each patient in time.
4

5. Survival Analysis
Notations:
: Time of event of interest.
: Censoring time.
: Observed time.
The event that occurred.
Hyp: Non-informative censoring:
Cumulative Incidence Function:
Survival Function:
T* ∈ ℝ+
C
T = min(T*, C)
Δ ∈ {0,1}
T* C|X
F*(ζ|x) = ℙ(T* ≤ ζ|X = x)
S*(ζ|x) = ℙ(T* > ζ|X = x)
Any given time
5

6. How to deal with the censoring distribution?
Inverse Propensity Censoring Weighting (IPCW)
• Compute the probability of being censored
• Weight samples by inverse probability
Time horizon
Less observed
outcomes
More weight
per person
(increasing censoring)
Many observed
outcomes
Less weight
per person
-> Learn and evaluate
6

7. Usual evaluation metrics
7

8. Integrated Brier Score
• Proper Scoring Rule
• “How close to the real probabilities are
our estimates?”
Lower is better
8
BS(t) =
1
n
n
∑
i=1
𝕀
(yi ≤ t ∧ δi = 1)
(0 − ̂
S(t|xi))2
̂
G(yi)
+
𝕀
(yi > t)
(1 − ̂
S(t|xi))2
̂
G(t)

9. C-index
Assess the ranking power of the models.
Commonly used by practitioners.
T*
i
≤ T*
j
⟶ S(τ|xi) < S(τ|xj)
9

10. Competing Risks
10

11. Competing risks setting
When there is only one event of interest (predict the death, recovery, etc.)
—> Survival Analysis
When there are multiple events (such as the cause of death, etc.).
—> Competing Risks Setting
11

12. Competing Risks Setting
Notations:
: Time of the
fi
rst event of interest.
: Censoring time.
: Observed time.
K: Number of events of interest.
The event that occurred.
Hyp: Non-informative censoring:
kth Cumulative Incidence Function:
T* ∈ ℝ+
C
T = min(T*, C)
Δ ∈ {0,1,...,K}
T* C|X
F*
k
(τ|x) = ℙ(T* ≤ τ ∩ Δ* = k|X = x)
Any given time
12
Buckets
Buckets
Perfect
calibratio
Model's CR
D-calibratio
Event 1
Aggregate results to obta
the D-CR calibration
Computation of the
probability of the event
at the true time event
Other event
observed
Event K
observed
CIFs
probability
CIFs
probability
Event K
Event 1
...
...

13. Motivation of our work
13

14. What do we want to achieve?
• Handles competing risks (limited results available).
• Predict the
fi
rst event for each patient correctly.
• Good trade-o
ff
between predictions and
fi
tting time.
• A model that handles tabular data well.
14

15. Survival Models:
Proper Scoring Rule and Stochastic
Optimization for Competing Risks
Published in AISTATS 2025
15

16. Proper scoring rule
• A scoring rule evaluates a distribution over an observation and gives a
corresponding score ( , ).
• The better the score, the better the model
fi
ts the observation.
Intuition:
Optimal proper scoring rule <-> Oracle distribution
ℓ
𝒫
Y
ℓ
𝒫
Y
16

17. Our proper Scoring rule
This can be givan to any estimator with stochastic optimization
Teaching a model how to survive 17

18. SurvivalBoost
• Implementation of the previous loss using Gradient Boosting Trees.
• Using a feedback loop to learn the distribution of .
C
SurvivalBoost Algorithm: one iteration
(Time is
sampled
uniformly.)
18

19. Our Benchmark
19

20. Metrics
• Mean of Integrated Brier Score
• C-index
• Introduction of the accuracy in time:
20
δi1ti≤τ
Highest probability
Number of non
censored individuals
Non
censored individuals

21. Competing Risks:
Benchmark
Trade-o
ff
prediction/training time Performances on the
mean IBS compared to
fi
tting time for each model on the
SEER dataset (300k datapoints)
Accuracy at time SEER dataset (300k datapoints)
21

22. Survival Analysis:
Benchmark
Trade-o
ff
prediction/training time in survival usage Performances on the IBS compared to
fi
tting time for each model.
22

23. Survival Analysis:
Scalability
Trade-o
ff
prediction/training time in survival usage Performances on the IBS compared to
fi
tting time for each model.
23

24. Python Library
The model is implemented in a Python
library named hazardous, which
includes documentation, examples, and
several useful metrics.
24

25. Conclusion
• A plug-in Proper Scoring Rule for competing risks and survival analysis.
• An implementation with Gradient Boosting Trees due to the presence of
categorical data.
• Outstanding performances in benchmarks in the competing risks and the survival
analysis setting
25

26. Future work
Submitted - Under review
We try to answer:
• What is the calibration in the competing risks setting?
• How to measure it?
• How to recalibrate any given method?
Tristan Haugomat
26