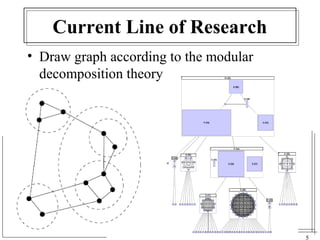
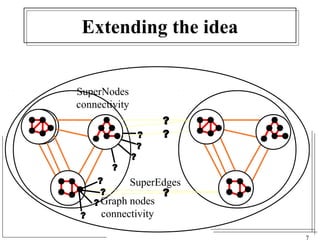
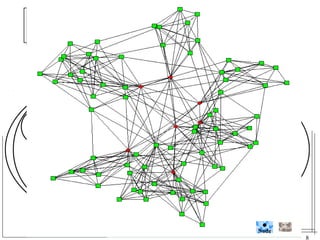
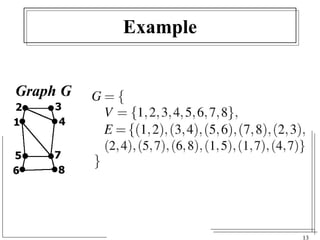
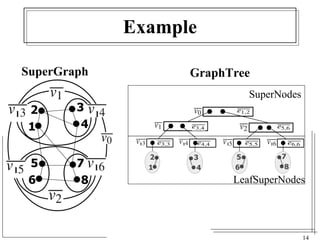
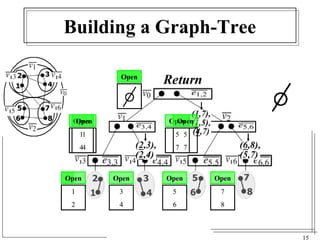
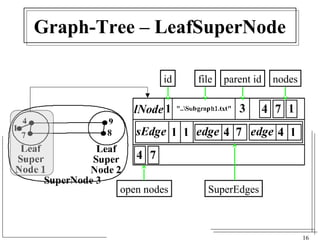
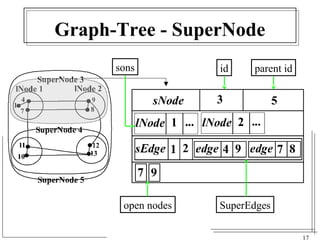
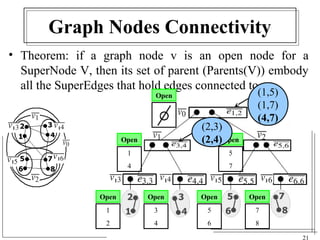
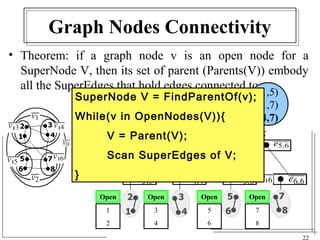
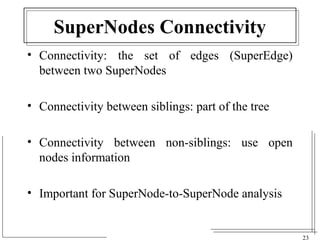
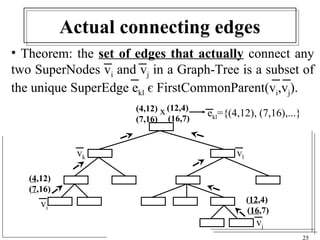
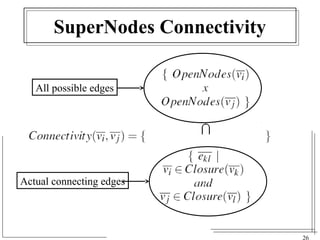
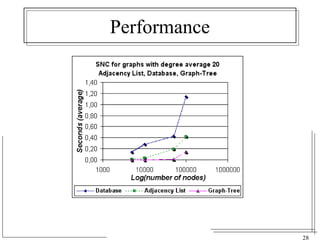
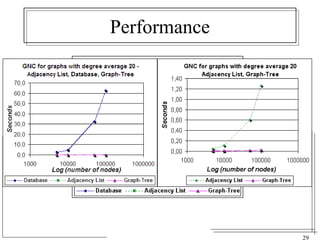
The document discusses the challenges of visualizing large graphs and presents a novel data structure called the supergraph and graph-tree, which allows for hierarchical management of graph partitions. It outlines principles for interactive visualization and connectivity, emphasizing the retention of original graph information while enhancing scalability. The conclusion introduces 'gmine,' a new graph visualization tool leveraging the proposed framework.

1. 1
SuperGraph Visualization
http://www.icmc.usp.br/~junio/PublishedPapers/RodriguesJr_et_al-ISM2006.pdf
José F. Rodrigues Jr., Agma J. M.
Traina, Caetano Traina Jr.
University of São Paulo
Computer Science Department
ICMC-USP
Brazil
Christos Faloutsos
Carnegie Mellon University
Computer Science Department
USA

2. 2
Outline
Problem and Principle
SuperGraphs and the Graph-Tree
Connectivity
Performance
Conclusions

3. 3
Problem
• Large graphs
– Hundred-thousand nodes or more
– Million edges magnitude
– web graphs, computer communication graphs ,
recommendation systems, whotrusts-whom
networks, bipartite graphs of web-logs
• Visual exploration limits
– Prohibitive processing power requirements for
interactive visualization
– Excessive number of graphical items in screen

4. 4
Problem
• Large graphs
– Hundred-thousand nodes or more
– Million edges magnitude
– web graphs, computer communication graphs ,
recommendation systems, whotrusts-whom
networks, bipartite graphs of web-logs
• Visual exploration limits
– Prohibitive processing power requirements for
interactive visualization
– Excessive number of graphical items in screen

5. 5
Current Line of Research
• Draw graph according to the modular
decomposition theory

6. 6
Current Line of Research
• Draw graph according Limitation
to the modular
decomposition theory
Graphs represented like this are limited:
- What is the relation between a given group of nodes
and another group of nodes?
- How many edges connect these two groups?
- Which are they?
- Which are the graph nodes from other groups that connect to a
graph node of interest?
The graph hierarchy is dead and the original is graph is lost.

7. 7
Extending the idea
?
?
?
SuperNodes
connectivity
?
?
?
?
?
??
SuperEdges
?
Graph nodes
connectivity

8. 8
Extending the idea
?
?
?
SuperNodes
connectivity
?
?
?
?
?
??
SuperEdges
?
Graph nodes
connectivity

9. 9
Principle
• Utilize compartmented processing and
presentation
• Utilize a structured partitioned version of
the graph to be analized
• Add interaction for a richer experience

10. 10
Principle
• Utilize compartmented Our proposal
processing and
presentation
Introduce a theory and a data structure to allow the use of the
hierarchical graph partition representation without loosing the
original • Utilize graph information.
a structured partitioned version of
the graph to be analized
Do this on the context of visualization, interaction and scalability
• Add interaction for a richer experience

11. 11
Outline
Problem and Principle
SuperGraphs and the Graph-Tree
Connectivity
Performance
Conclusions

12. 12
SuperGraphs and the Graph-Tree
• Given a graph G={V,E} a SuperGrap is a recursive
partitioning of G
• A GraphTree is a SuperGraph structured as a tree
• Graph nodes are kept at the leaf nodes of the tree
• Graph edges are distributed along the tree structure

13. 13
Example

14. 14
Example
SuperGraph GraphTree
SuperNodes
LeafSuperNodes

15. 15
Building a Graph-Tree
Open
Open
Open
1
2
Open
3
4
Open
Open
Open
5
6
Open
7
8
1
4
5
7
Open
1
4
5
7

16. 16
Graph-Tree – LeafSuperNode
id file parent id nodes
open nodes SuperEdges

17. 17
Graph-Tree - SuperNode
id parent id
sons
open nodes SuperEdges

18. 18
Graph-Tree
• A tree of graph partitions or a hierarchical
partitioning of a graph
• A new data structure for graphs
• Benefits: novel graph storage + structured graph
partitions
• Provides: on demand processing/presentation +
inter partitions edges information + spatial search
tree (natural R-Tree properties)

19. 19
Outline
Problem and Principle
SuperGraphs and the Graph-Tree
Connectivity
Performance
Conclusions

20. 20
Outline
Problem and Principle
SuperGraphs and the Graph-Tree
Connectivity
Performance
Conclusions

21. 21
Graph Nodes Connectivity
• Theorem: if a graph node v is an open node for a
SuperNode V, then its set of parent (Parents(V)) embody
all the SuperEdges that hold edges connected to v.
Open
1
2
Open
3
4
Open
5
6
Open
7
8
Open
1
4
Open
5
7
Open
(2,3)
(2,4)
(1,5)
(1,7)
(4,7)

22. 22
Graph Nodes Connectivity
• Theorem: if a graph node v is an open node for a
SuperNode V, then its set of parent (Parents(V)) embody
all the SuperEdges that hold edges connected to v.
Open
1
2
Open
3
4
Open
5
6
Open
7
8
Open
1
4
Open
5
7
Open
(2,3)
(2,4)
(1,5)
(1,7)
(4,7)
SuperNode V = FindParentOf(v);
While(v in OpenNodes(V)){
V = Parent(V);
Scan SuperEdges of V;
}

23. 23
SuperNodes Connectivity
• Connectivity: the set of edges (SuperEdge)
between two SuperNodes
• Connectivity between siblings: part of the tree
• Connectivity between non-siblings: use open
nodes information
• Important for SuperNode-to-SuperNode analysis

24. 24
All possible edges
• The open nodes information specifies all the
nodes of a given SuperNode that connect to
nodes from other SuperNodes
• Theorem: given two SuperNodes vi and vj, the Cartesian
product OpenNodes(vi) x OpenNodes(vj) determines the
set of all possible edges between SuperNodes vi and vj.

25. 25
Actual connecting edges
• Theorem: the set of edges that actually connect any
two SuperNodes vi and vj in a Graph-Tree is a subset of
the unique SuperEdge ekl є FirstCommonParent(vi,vj).
vi
ekl={(4,12), (7,16),...}
(12,4)
(16,7)
vj
(4,12)
(7,16)
(12,4)
(16,7)
(4,12)
(7,16)
x
vk vl

26. 26
SuperNodes Connectivity
All possible edges
Actual connecting edges

27. 27
Outline
Problem and Principle
SuperGraphs and the Graph-Tree
Connectivity
Performance
Conclusions

28. 28
Performance

29. 29
Performance

30. 30
Short Demonstration

31. 31
Outline
Problem and Principle
SuperGraphs and the Graph-Tree
Connectivity
Performance
Conclusions

32. 32
Conclusion
• A new data structure for graphs
– hierarchical management of graph partitions
(More SuperNodes)
at http://www.cs.cmu.edu/~junio
– the original graph information is not lost
– relationship (SuperEdges) between groups of nodes
instead of nodes only
– scalability for visualization and interaction
• GMine - A new graph visualization tool

33. 33
End