Patrick Michl, profile picture
Uploaded byPatrick Michl
PDF, PPTX22 views

Structure learning with Deep Autoencoders

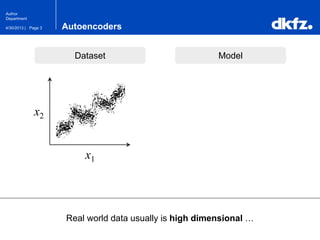
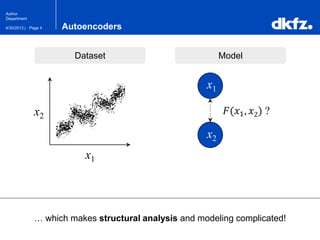
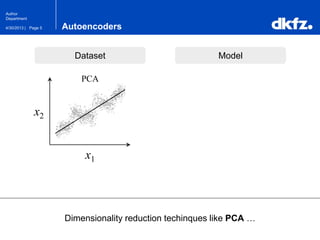
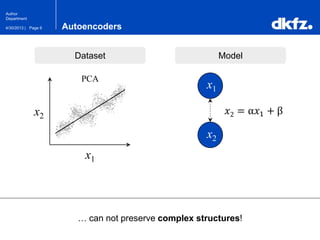
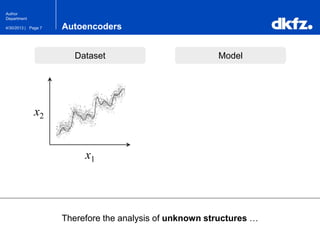
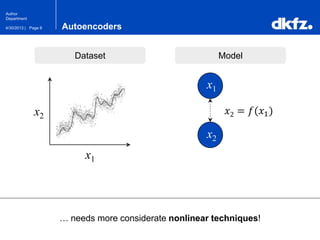
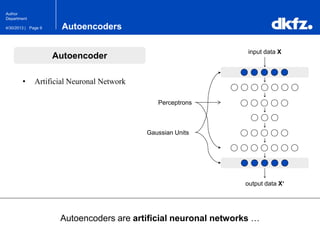
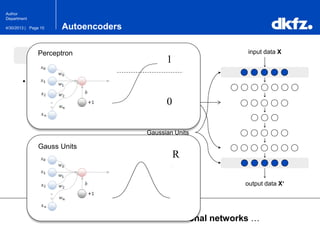
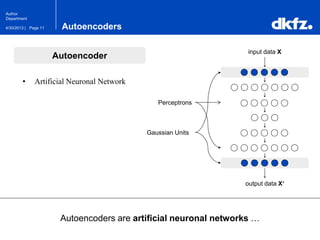
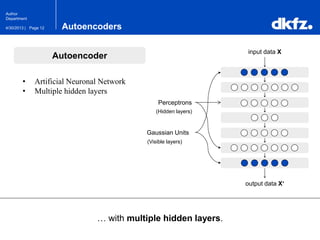
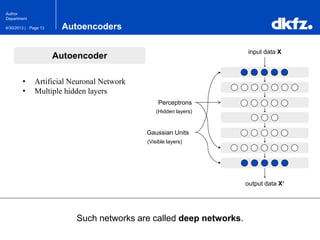
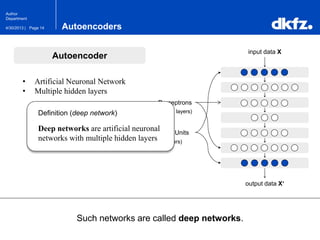
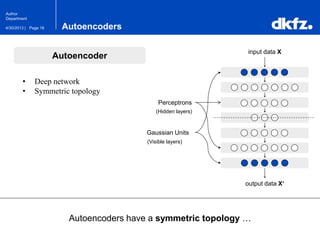
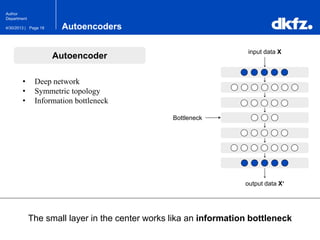
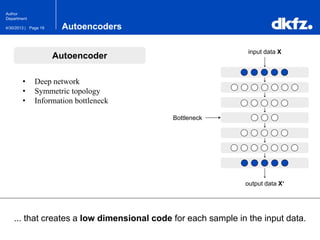
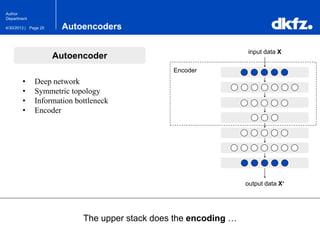
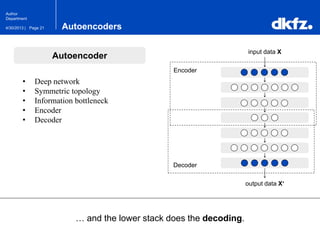
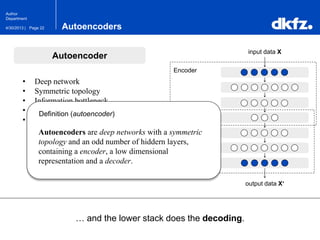
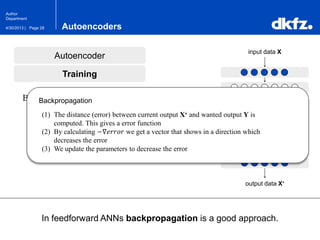
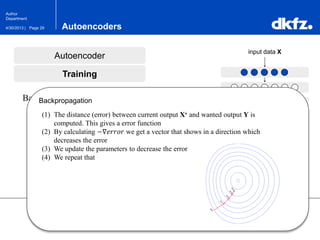
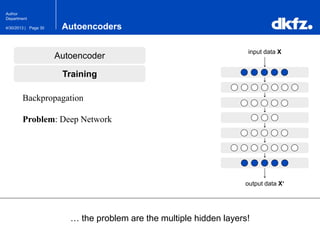
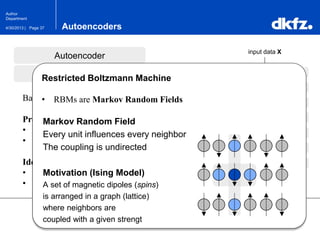
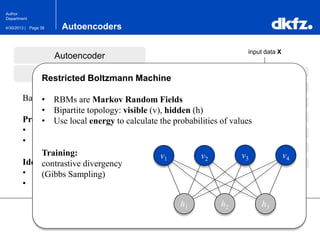
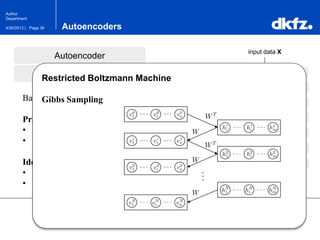
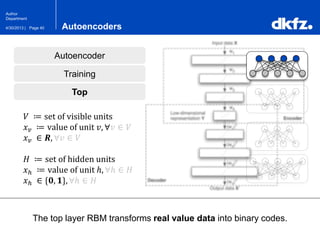
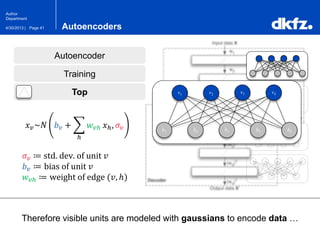
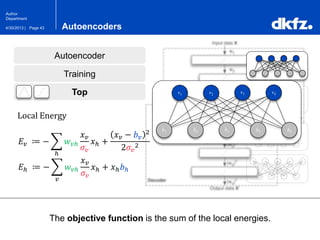
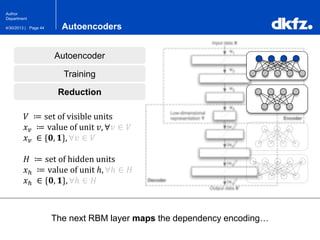
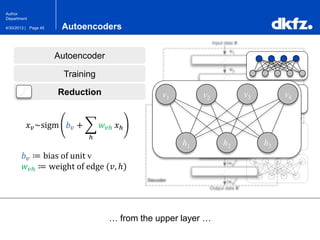
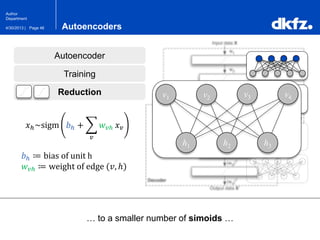
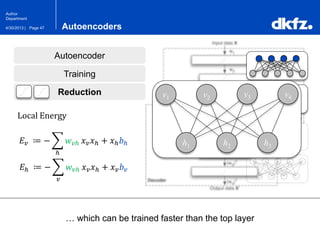
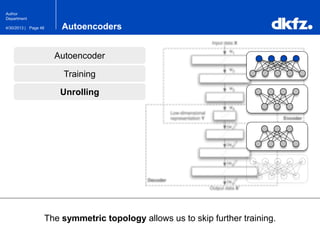
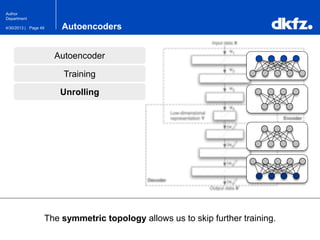
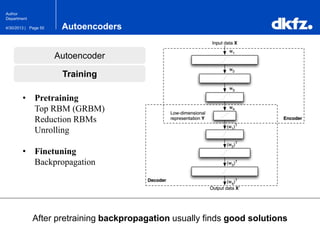
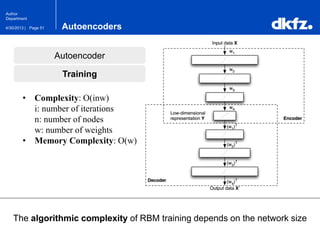
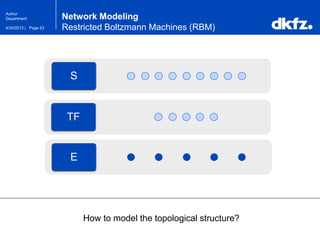
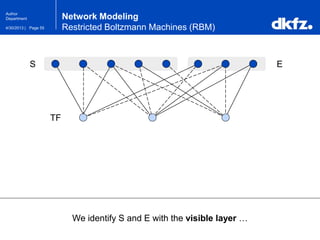
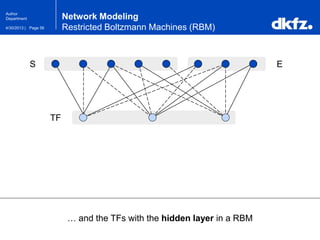
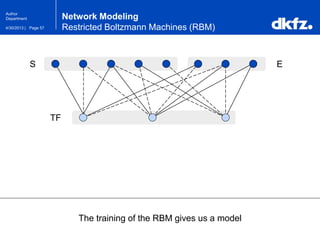
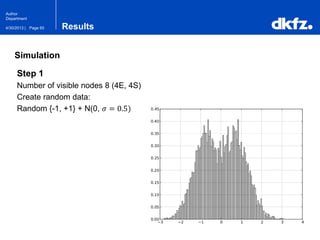
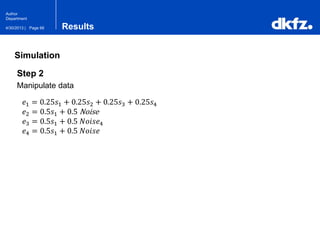
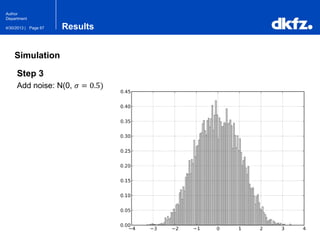
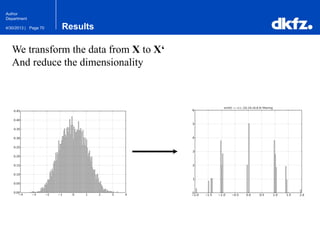
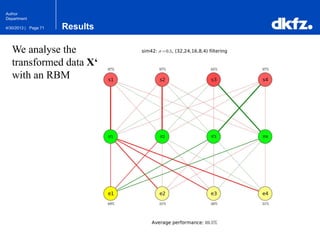
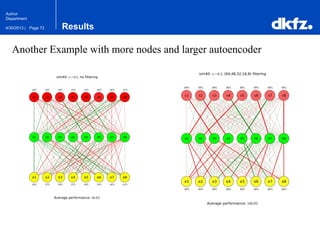
The document discusses the use of deep autoencoders for structural learning and modeling, emphasizing their ability to handle high-dimensional data through dimensionality reduction techniques. It outlines the architecture of autoencoders, including the encoding and decoding processes, and the importance of pretraining with Restricted Boltzmann Machines (RBMs) to improve training efficiency. The document also presents results related to the validation and implementation of autoencoders using artificial datasets to assess performance.

Embed presentation

Download as PDF, PPTX
Structure learning with deep autoencoders Network Modeling Seminar, 30/4/2013 Patrick Michl
Page 24/30/2013 | Author Department Agenda Autoencoders Biological Model Validation & Implementation
Page 34/30/2013 | Author Department Real world data usually is high dimensional … x1 x2 Dataset Model Autoencoders
Page 44/30/2013 | Author Department … which makes structural analysis and modeling complicated! x1 x2 x1 x2 Dataset Model 𝐹(𝑥1, 𝑥2) ? Autoencoders
Page 54/30/2013 | Author Department Dimensionality reduction techinques like PCA … x1 x2 PCA Dataset Model Autoencoders
Page 64/30/2013 | Author Department … can not preserve complex structures! x1 x2 PCA Dataset Model x1 x2 𝑥2 = α𝑥1 + β Autoencoders
Page 74/30/2013 | Author Department Therefore the analysis of unknown structures … x1 x2 Dataset Model Autoencoders
Page 84/30/2013 | Author Department … needs more considerate nonlinear techniques! x1 x2 Dataset Model x1 x2 𝑥2 = 𝑓(𝑥1) Autoencoders
Page 94/30/2013 | Author Department Autoencoders are artificial neuronal networks … Autoencoder • Artificial Neuronal Network Autoencoders input data X output data X‘ Perceptrons Gaussian Units
Page 104/30/2013 | Author Department Autoencoders are artificial neuronal networks … Autoencoder • Artificial Neuronal Network Autoencoders input data X output data X‘ Perceptrons Gaussian Units Perceptron 1 0 Gauss Units R
Page 114/30/2013 | Author Department Autoencoders are artificial neuronal networks … Autoencoder • Artificial Neuronal Network Autoencoders input data X output data X‘ Perceptrons Gaussian Units
Page 124/30/2013 | Author Department Autoencoder • Artificial Neuronal Network • Multiple hidden layers Autoencoders … with multiple hidden layers. Gaussian Units input data X output data X‘ Perceptrons (Visible layers) (Hidden layers)
Page 134/30/2013 | Author Department Autoencoder • Artificial Neuronal Network • Multiple hidden layers Autoencoders Such networks are called deep networks. Gaussian Units input data X output data X‘ Perceptrons (Visible layers) (Hidden layers)
Page 144/30/2013 | Author Department Autoencoder • Artificial Neuronal Network • Multiple hidden layers Autoencoders Such networks are called deep networks. Gaussian Units input data X output data X‘ Perceptrons (Visible layers) (Hidden layers)Definition (deep network) Deep networks are artificial neuronal networks with multiple hidden layers
Page 154/30/2013 | Author Department Autoencoder Autoencoders Gaussian Units input data X output data X‘ Perceptrons (Visible layers) (Hidden layers) Such networks are called deep networks. • Deep network
Page 164/30/2013 | Author Department Autoencoder Autoencoders Autoencoders have a symmetric topology … Gaussian Units input data X output data X‘ Perceptrons (Visible layers) (Hidden layers) • Deep network • Symmetric topology
Page 174/30/2013 | Author Department Autoencoder Autoencoders … with an odd number of hidden layers. Gaussian Units input data X output data X‘ Perceptrons (Visible layers) (Hidden layers) • Deep network • Symmetric topology
Page 184/30/2013 | Author Department Autoencoder Autoencoders The small layer in the center works lika an information bottleneck input data X output data X‘ • Deep network • Symmetric topology • Information bottleneck Bottleneck
Page 194/30/2013 | Author Department Autoencoder Autoencoders ... that creates a low dimensional code for each sample in the input data. input data X output data X‘ • Deep network • Symmetric topology • Information bottleneck Bottleneck
Page 204/30/2013 | Author Department Autoencoder Autoencoders The upper stack does the encoding … input data X output data X‘ • Deep network • Symmetric topology • Information bottleneck • Encoder Encoder
Page 214/30/2013 | Author Department Autoencoder Autoencoders … and the lower stack does the decoding. input data X output data X‘ • Deep network • Symmetric topology • Information bottleneck • Encoder • Decoder Encoder Decoder
Page 224/30/2013 | Author Department • Deep network • Symmetric topology • Information bottleneck • Encoder • Decoder Autoencoder Autoencoders … and the lower stack does the decoding. input data X output data X‘ Encoder Decoder Definition (deep network) Deep networks are artificial neuronal networks with multiple hidden layers Definition (autoencoder) Autoencoders are deep networks with a symmetric topology and an odd number of hiddern layers, containing a encoder, a low dimensional representation and a decoder.
Page 234/30/2013 | Author Department Autoencoder Autoencoders Autoencoders can be used to reduce the dimension of data … input data X output data X‘ Problem: dimensionality of data Idea: 1. Train autoencoder to minimize the distance between input X and output X‘ 2. Encode X to low dimensional code Y 3. Decode low dimensional code Y to output X‘ 4. Output X‘ is low dimensional
Page 244/30/2013 | Author Department Autoencoder Autoencoders … if we can train them! input data X output data X‘ Problem: dimensionality of data Idea: 1. Train autoencoder to minimize the distance between input X and output X‘ 2. Encode X to low dimensional code Y 3. Decode low dimensional code Y to output X‘ 4. Output X‘ is low dimensional
Page 254/30/2013 | Author Department Autoencoder Autoencoders In feedforward ANNs backpropagation is a good approach. input data X output data X‘ Training Backpropagation
Page 264/30/2013 | Author Department Backpropagation Autoencoder Autoencoders input data X output data X‘ Training Definition (autoencoder) Backpropagation (1) The distance (error) between current output X‘ and wanted output Y is computed. This gives a error function 𝑋′ = 𝐹 𝑋 error = 𝑋′2 − 𝑌 In feedforward ANNs backpropagation is a good approach.
Page 274/30/2013 | Author Department Backpropagation Autoencoder Autoencoders In feedforward ANNs backpropagation is the choice input data X output data X‘ Training Definition (autoencoder) Backpropagation (1) The distance (error) between current output X‘ and wanted output Y is computed. This gives a error function Example (linear neuronal unit with two inputs)
Page 284/30/2013 | Author Department Backpropagation Autoencoder Autoencoders input data X output data X‘ Training Definition (autoencoder) Backpropagation (1) The distance (error) between current output X‘ and wanted output Y is computed. This gives a error function (2) By calculating −∇𝑒𝑟𝑟𝑜𝑟 we get a vector that shows in a direction which decreases the error (3) We update the parameters to decrease the error In feedforward ANNs backpropagation is a good approach.
Page 294/30/2013 | Author Department Backpropagation Autoencoder Autoencoders In feedforward ANNs backpropagation is the choice input data X output data X‘ Training Definition (autoencoder) Backpropagation (1) The distance (error) between current output X‘ and wanted output Y is computed. This gives a error function (2) By calculating −∇𝑒𝑟𝑟𝑜𝑟 we get a vector that shows in a direction which decreases the error (3) We update the parameters to decrease the error (4) We repeat that
Page 304/30/2013 | Author Department Autoencoder Autoencoders … the problem are the multiple hidden layers! input data X output data X‘ Training Backpropagation Problem: Deep Network
Page 314/30/2013 | Author Department Autoencoder Autoencoders input data X output data X‘ Training Backpropagation is known to be slow far away from the output layer … Backpropagation Problem: Deep Network • Very slow training
Page 324/30/2013 | Author Department Autoencoder Autoencoders input data X output data X‘ Training … and can converge to poor local minima. Backpropagation Problem: Deep Network • Very slow training • Maybe bad solution
Page 334/30/2013 | Author Department Autoencoder Autoencoders input data X output data X‘ Training Backpropagation Problem: Deep Network • Very slow training • Maybe bad solution Idea: Initialize close to a good solution The task is to initialize the parameters close to a good solution!
Page 344/30/2013 | Author Department Autoencoder Autoencoders input data X output data X‘ Training Backpropagation Problem: Deep Network • Very slow training • Maybe bad solution Idea: Initialize close to a good solution • Pretraining Therefore the training of autoencoders has a pretraining phase …
Page 354/30/2013 | Author Department Autoencoder Autoencoders input data X output data X‘ Training Backpropagation Problem: Deep Network • Very slow training • Maybe bad solution Idea: Initialize close to a good solution • Pretraining • Restricted Boltzmann Machines … which uses Restricted Boltzmann Machines (RBMs)
Page 364/30/2013 | Author Department Autoencoder Autoencoders input data X output data X‘ Training Backpropagation Problem: Deep Network • Very slow training • Maybe bad solution Idea: Initialize close to a good solution • Pretraining • Restricted Boltzmann Machines … which uses Restricted Boltzmann Machines (RBMs) Restricted Boltzmann Machine • RBMs are Markov Random Fields
Page 374/30/2013 | Author Department Autoencoder Autoencoders input data X output data X‘ Training Backpropagation Problem: Deep Network • Very slow training • Maybe bad solution Idea: Initialize close to a good solution • Pretraining • Restricted Boltzmann Machines … which uses Restricted Boltzmann Machines (RBMs) Restricted Boltzmann Machine • RBMs are Markov Random Fields Markov Random Field Every unit influences every neighbor The coupling is undirected Motivation (Ising Model) A set of magnetic dipoles (spins) is arranged in a graph (lattice) where neighbors are coupled with a given strengt
Page 384/30/2013 | Author Department Autoencoder Autoencoders input data X output data X‘ Training Backpropagation Problem: Deep Network • Very slow training • Maybe bad solution Idea: Initialize close to a good solution • Pretraining • Restricted Boltzmann Machines … which uses Restricted Boltzmann Machines (RBMs) Restricted Boltzmann Machine • RBMs are Markov Random Fields • Bipartite topology: visible (v), hidden (h) • Use local energy to calculate the probabilities of values Training: contrastive divergency (Gibbs Sampling) h1 v1 v2 v3 v4 h2 h3
Page 394/30/2013 | Author Department Autoencoder Autoencoders input data X output data X‘ Training Backpropagation Problem: Deep Network • Very slow training • Maybe bad solution Idea: Initialize close to a good solution • Pretraining • Restricted Boltzmann Machines … which uses Restricted Boltzmann Machines (RBMs) Restricted Boltzmann Machine Gibbs Sampling
Page 404/30/2013 | Author Department Autoencoders Autoencoder The top layer RBM transforms real value data into binary codes. 𝑉 ≔ set of visible units 𝑥 𝑣 ≔ value of unit 𝑣, ∀𝑣 ∈ 𝑉 𝑥 𝑣 ∈ 𝑹, ∀𝑣 ∈ 𝑉 𝐻 ≔ set of hidden units 𝑥ℎ ≔ value of unit ℎ, ∀ℎ ∈ 𝐻 𝑥ℎ ∈ {𝟎, 𝟏}, ∀ℎ ∈ 𝐻 Top Training
Page 414/30/2013 | Author Department Autoencoders Autoencoder Top Therefore visible units are modeled with gaussians to encode data … 𝑥 𝑣~𝑁 𝑏 𝑣 + 𝑤 𝑣ℎ ℎ 𝑥ℎ, 𝜎𝑣 𝜎𝑣 ≔ std. dev. of unit 𝑣 𝑏 𝑣 ≔ bias of unit 𝑣 𝑤 𝑣ℎ ≔ weight of edge (𝑣, ℎ) h2 v1 v2 v3 v4 h3 h4 h5h1 Training
Page 424/30/2013 | Author Department Autoencoders Autoencoder Top … and many hidden units with simoids to encode dependencies 𝑥ℎ~sigm 𝑏ℎ + 𝑤 𝑣ℎ 𝑣 𝑥 𝑣 𝜎𝑣 𝜎𝑣 ≔ std. dev. of unit 𝑣 𝑏ℎ ≔ bias of unit ℎ 𝑤 𝑣ℎ ≔ weight of edge (𝑣, ℎ) h2 v1 v2 v3 v4 h3 h4 h5h1 Training
Page 434/30/2013 | Author Department Autoencoders Autoencoder Top The objective function is the sum of the local energies. Local Energy 𝐸ℎ ≔ − 𝑤 𝑣ℎ 𝑣 𝑥 𝑣 𝜎𝑣 𝑥ℎ + 𝑥ℎ 𝑏ℎ 𝐸 𝑣 ≔ − 𝑤 𝑣ℎ ℎ 𝑥 𝑣 𝜎𝑣 𝑥ℎ + 𝑥 𝑣 − 𝑏 𝑣 2 2𝜎𝑣 2 h2 v1 v2 v3 v4 h3 h4 h5h1 Training
Page 444/30/2013 | Author Department Autoencoders Autoencoder Reduction 𝑉 ≔ set of visible units 𝑥 𝑣 ≔ value of unit 𝑣, ∀𝑣 ∈ 𝑉 𝑥 𝑣 ∈ {𝟎, 𝟏}, ∀𝑣 ∈ 𝑉 𝐻 ≔ set of hidden units 𝑥ℎ ≔ value of unit ℎ, ∀ℎ ∈ 𝐻 𝑥ℎ ∈ {𝟎, 𝟏}, ∀ℎ ∈ 𝐻 The next RBM layer maps the dependency encoding… Training
Page 454/30/2013 | Author Department Autoencoders Autoencoder Reduction … from the upper layer … 𝑥 𝑣~sigm 𝑏 𝑣 + 𝑤 𝑣ℎ ℎ 𝑥ℎ 𝑏 𝑣 ≔ bias of unit v 𝑤 𝑣ℎ ≔ weight of edge (𝑣, ℎ) h1 v1 v2 v3 v4 h2 h3 Training
Page 464/30/2013 | Author Department Autoencoders Autoencoder Reduction … to a smaller number of simoids … 𝑥ℎ~sigm 𝑏ℎ + 𝑤 𝑣ℎ 𝑣 𝑥 𝑣 𝑏ℎ ≔ bias of unit h 𝑤 𝑣ℎ ≔ weight of edge (𝑣, ℎ) h1 v1 v2 v3 v4 h2 h3 Training
Page 474/30/2013 | Author Department Autoencoders Autoencoder Reduction … which can be trained faster than the top layer Local Energy 𝐸 𝑣 ≔ − 𝑤 𝑣ℎ ℎ 𝑥 𝑣 𝑥ℎ + 𝑥ℎ 𝑏ℎ 𝐸ℎ ≔ − 𝑤 𝑣ℎ 𝑣 𝑥 𝑣 𝑥ℎ + 𝑥 𝑣 𝑏 𝑣 h1 v1 v2 v3 v4 h2 h3 Training
Page 484/30/2013 | Author Department Autoencoders Autoencoder Unrolling The symmetric topology allows us to skip further training. Training
Page 494/30/2013 | Author Department Autoencoders Autoencoder Unrolling The symmetric topology allows us to skip further training. Training
Page 504/30/2013 | Author Department After pretraining backpropagation usually finds good solutions Autoencoders Autoencoder Training • Pretraining Top RBM (GRBM) Reduction RBMs Unrolling • Finetuning Backpropagation
Page 514/30/2013 | Author Department The algorithmic complexity of RBM training depends on the network size Autoencoders Autoencoder Training • Complexity: O(inw) i: number of iterations n: number of nodes w: number of weights • Memory Complexity: O(w)
Page 524/30/2013 | Author Department Agenda Autoencoders Biological Model Validation & Implementation
Page 534/30/2013 | Author Department Network Modeling Restricted Boltzmann Machines (RBM) How to model the topological structure? S E TF
Page 544/30/2013 | Author Department We define S and E as visible data Layer … S E TF Network Modeling Restricted Boltzmann Machines (RBM)
Page 554/30/2013 | Author Department S E TF Network Modeling Restricted Boltzmann Machines (RBM) We identify S and E with the visible layer …
Page 564/30/2013 | Author Department S E … and the TFs with the hidden layer in a RBM TF Network Modeling Restricted Boltzmann Machines (RBM)
Page 574/30/2013 | Author Department S E The training of the RBM gives us a model TF Network Modeling Restricted Boltzmann Machines (RBM)
Page 584/30/2013 | Author Department Agenda Autoencoder Biological Model Implementation & Results
Page 594/30/2013 | Author Department Results Validation of the results • Needs information about the true regulation • Needs information about the descriptive power of the data
Page 604/30/2013 | Author Department Results Validation of the results • Needs information about the true regulation • Needs information about the descriptive power of the data Without this infomation validation can only be done, using artificial datasets!
Page 614/30/2013 | Author Department Results Artificial datasets We simulate data in three steps:
Page 624/30/2013 | Author Department Results Artificial datasets We simulate data in three steps Step 1 Choose number of Genes (E+S) and create random bimodal distributed data
Page 634/30/2013 | Author Department Results Artificial datasets We simulate data in three steps Step 1 Choose number of Genes (E+S) and create random bimodal distributed data Step 2 Manipulate data in a fixed order
Page 644/30/2013 | Author Department Results Artificial datasets We simulate data in three steps Step 1 Choose number of Genes (E+S) and create random bimodal distributed data Step 2 Manipulate data in a fixed order Step 3 Add noise to manipulated data and normalize data
Page 654/30/2013 | Author Department Simulation Results Step 1 Number of visible nodes 8 (4E, 4S) Create random data: Random {-1, +1} + N(0, 𝜎 = 0.5)
Page 664/30/2013 | Author Department Simulation Results 𝑒1 = 0.25𝑠1 + 0.25𝑠2 + 0.25𝑠3 + 0.25𝑠4 𝑒2 = 0.5𝑠1 + 0.5 Noise 𝑒3 = 0.5𝑠1 + 0.5 𝑁𝑜𝑖𝑠𝑒4 𝑒4 = 0.5𝑠1 + 0.5 𝑁𝑜𝑖𝑠𝑒 Step 2 Manipulate data
Page 674/30/2013 | Author Department Simulation Results Step 3 Add noise: N(0, 𝜎 = 0.5)
Page 684/30/2013 | Author Department Results We analyse the data X with an RBM
Page 694/30/2013 | Author Department Results We train an autoencoder with 9 hidden layers and 165 nodes: Layer 1 & 9: 32 hidden units Layer 2 & 8: 24 hidden units Layer 3 & 7: 16 hidden units Layer 4 & 6: 8 hidden units Layer 5: 5 hidden units input data X output data X‘
Page 704/30/2013 | Author Department Results We transform the data from X to X‘ And reduce the dimensionality
Page 714/30/2013 | Author Department Results We analyse the transformed data X‘ with an RBM
Page 724/30/2013 | Author Department Results Lets compare the models
Page 734/30/2013 | Author Department Results Another Example with more nodes and larger autoencoder
Page 744/30/2013 | Author Department Conclusion Conclusion • Autoencoders can improve modeling significantly by reducing the dimensionality of data • Autoencoders preserve complex structures in their multilayer perceptron network. Analysing those networks (for example with knockout tests) could give more structural information • The drawback are high computational costs Since the field of deep learning is getting more popular (Face recognition / Voice recognition, Image transformation). Many new improvements in facing the computational costs have been made.
Page 754/30/2013 | Author Department Acknowledgement eilsLABS PD Dr. Rainer König Prof. Dr Roland Eils Network Modeling Group

More Related Content

PDF
Structure learning with Deep Neural Networks
byPatrick Michl
 
PDF
Structure learning with Deep Neural Networks
byPatrick Michl
 
PPTX
UNIT-4.pptx
byNiharikaThakur32
 
PDF
UNIT-4.pdf
byNiharikaThakur32
 
PDF
UNIT-4.pdf
byNiharikaThakur32
 
PPTX
Deep learning from a novice perspective
byAnirban Santara
 
PDF
Autoencoders
byCloudxLab
 
PDF
Review_Cibe Sridharan
byCibe Sridharan
 
Structure learning with Deep Neural Networks
byPatrick Michl
 
Structure learning with Deep Neural Networks
byPatrick Michl
 
UNIT-4.pptx
byNiharikaThakur32
 
UNIT-4.pdf
byNiharikaThakur32
 
UNIT-4.pdf
byNiharikaThakur32
 
Deep learning from a novice perspective
byAnirban Santara
 
Autoencoders
byCloudxLab
 
Review_Cibe Sridharan
byCibe Sridharan
 

Similar to Structure learning with Deep Autoencoders

PDF
Fundamental of deep learning
byStanley Wang
 
PDF
Sparse autoencoder
byDevashish Patel
 
PPTX
Deep Learning A-Z™: AutoEncoders - Module 6
byKirill Eremenko
 
PDF
Separating Hype from Reality in Deep Learning with Sameer Farooqui
byDatabricks
 
PPTX
Autoencoders for image_classification
byCenk Bircanoğlu
 
PPTX
Introduction to Autoencoders: Types and Applications
byAmr Rashed
 
PDF
Deep Learning Study _ FInalwithCNN_RNN_LSTM_GRU.pdf
bynaveenraghavendran10
 
PPTX
Piotr Mirowski - Review Autoencoders (Deep Learning) - CIUUK14
byDaniel Lewis
 
PPTX
Introduction to un supervised learning
byRishikesh .
 
PDF
Deep into to Deep Learning Starting from Basics
byPlusOrMinusZero
 
PDF
Understanding Deep Learning & Parameter Tuning with MXnet, H2o Package in R
byManish Saraswat
 
PPTX
Artificial neural networks
byShwethaShreeS
 
PDF
Neural Networks on Steroids (Poster)
byAdam Blevins
 
PDF
Deep Style: Using Variational Auto-encoders for Image Generation
byTJ Torres
 
PDF
A Survey of Deep Learning Algorithms for Malware Detection
byIJCSIS Research Publications
 
PDF
Deep learning - a primer
byUwe Friedrichsen
 
PDF
Deep learning - a primer
byShirin Elsinghorst
 
PDF
Autoencoder
byHARISH R
 
PPTX
Artificial Neural Networks ppt.pptx for final sem cse
byNaveenBhajantri1
 
PDF
unit 1- NN concpts.pptx.pdf withautomstion
byKarthickGanesh8
 
Fundamental of deep learning
byStanley Wang
 
Sparse autoencoder
byDevashish Patel
 
Deep Learning A-Z™: AutoEncoders - Module 6
byKirill Eremenko
 
Separating Hype from Reality in Deep Learning with Sameer Farooqui
byDatabricks
 
Autoencoders for image_classification
byCenk Bircanoğlu
 
Introduction to Autoencoders: Types and Applications
byAmr Rashed
 
Deep Learning Study _ FInalwithCNN_RNN_LSTM_GRU.pdf
bynaveenraghavendran10
 
Piotr Mirowski - Review Autoencoders (Deep Learning) - CIUUK14
byDaniel Lewis
 
Introduction to un supervised learning
byRishikesh .
 
Deep into to Deep Learning Starting from Basics
byPlusOrMinusZero
 
Understanding Deep Learning & Parameter Tuning with MXnet, H2o Package in R
byManish Saraswat
 
Artificial neural networks
byShwethaShreeS
 
Neural Networks on Steroids (Poster)
byAdam Blevins
 
Deep Style: Using Variational Auto-encoders for Image Generation
byTJ Torres
 
A Survey of Deep Learning Algorithms for Malware Detection
byIJCSIS Research Publications
 
Deep learning - a primer
byUwe Friedrichsen
 
Deep learning - a primer
byShirin Elsinghorst
 
Autoencoder
byHARISH R
 
Artificial Neural Networks ppt.pptx for final sem cse
byNaveenBhajantri1
 
unit 1- NN concpts.pptx.pdf withautomstion
byKarthickGanesh8
 

More from Patrick Michl

PDF
Attention Please! 2022
byPatrick Michl
 
PDF
Spec2Vec - Energy based non-linear Calibration in NIRS
byPatrick Michl
 
PDF
Attention please! Attention Mechanism in Neural Networks
byPatrick Michl
 
PDF
Regulation Analysis using Restricted Boltzmann Machines
byPatrick Michl
 
PDF
Concept of Regulation Analysis using Restricted Boltzmann Machines
byPatrick Michl
 
PDF
Synchronization and Collective Dynamics
byPatrick Michl
 
PDF
Epidemic Spreading
byPatrick Michl
 
Attention Please! 2022
byPatrick Michl
 
Spec2Vec - Energy based non-linear Calibration in NIRS
byPatrick Michl
 
Attention please! Attention Mechanism in Neural Networks
byPatrick Michl
 
Regulation Analysis using Restricted Boltzmann Machines
byPatrick Michl
 
Concept of Regulation Analysis using Restricted Boltzmann Machines
byPatrick Michl
 
Synchronization and Collective Dynamics
byPatrick Michl
 
Epidemic Spreading
byPatrick Michl
 

Recently uploaded

PDF
Machine Learning Lectures -- Support Vector Machine (SVM)
byZahra Sadeghi
 
PPTX
Data Collection and data types Chapter 2.pptx
byModern College Shivajinagar, Pune-5
 
PPT
Ch04uiuuuuuuuuuuuuuuuuuuuuuukkkkkkklh.ppt
bykarzanberdawood
 
PDF
Bettersize | Absolute Molecular Weight Determination of HSAs using the BeSEC
byBettersize Instruments
 
PDF
Alkane ( एल्केन ) - Notes PDF Download Hindi Medium - IRFANULLAH MEHAR.pdf
byWorld of Wisdom
 
PPTX
ORGANIC CHEMISTRY PRESENTATION WEEK 3 and 4
byJohnRenier1
 
PPTX
F4 chapter 2.1-Cpr-Powerpoint Cardiopulmonary resuscitation use for emergency...
byYeohLeemoi48
 
PPTX
Unit_49_Class_1_Systems_Integration.pptx
bynehaijaz13
 
PPT
plant Photosynthesis and leaf structure.ppt
byEnas813292
 
PPTX
LOWER LIMB ANATOMY notes for GROSS ANATOMY
bymarkmutugi44
 
PDF
UNIT I Stereoisomerism (Pharmaceutical Organic Chemistry III)
byssjsphs
 
PPTX
Annual Report of CMC filed in the USFDA for NDA & ANDA
byPHARMA IQ EDUCATION
 
PPTX
Aerobic-and-Anaerobic-Digesters-Biological-Waste-Treatment-Technologies.pptx
byShanmugaPriya168919
 
PDF
Basic Principles of Plant Pathology; Entomology & Nematology in Plant Patholo...
byNistarini College, Purulia (W.B) India
 
PDF
Bioremedation - Dechlorination ,Types and process , advantage and disadvantage
byswathijagadeesan1402
 
PDF
Betterszie | Exploring Dendrimer Generations Using the BeSEC
byBettersize Instruments
 
PPTX
Light compensation point, CO2 compensation point, Quantum yield in plants.pptx
byRashmiMG2
 
PDF
PHYTOREMEDIATION OF HEAVY METALS IN SOIL
byswethaviji2005
 
PDF
Machine Learning Lectures --- Likelihood
byZahra Sadeghi
 
PPTX
TOPIC - DROUGHT PRIMING AND STRESS MEMORY
byAbhishekkumawat67
 
Machine Learning Lectures -- Support Vector Machine (SVM)
byZahra Sadeghi
 
Data Collection and data types Chapter 2.pptx
byModern College Shivajinagar, Pune-5
 
Ch04uiuuuuuuuuuuuuuuuuuuuuuukkkkkkklh.ppt
bykarzanberdawood
 
Bettersize | Absolute Molecular Weight Determination of HSAs using the BeSEC
byBettersize Instruments
 
Alkane ( एल्केन ) - Notes PDF Download Hindi Medium - IRFANULLAH MEHAR.pdf
byWorld of Wisdom
 
ORGANIC CHEMISTRY PRESENTATION WEEK 3 and 4
byJohnRenier1
 
F4 chapter 2.1-Cpr-Powerpoint Cardiopulmonary resuscitation use for emergency...
byYeohLeemoi48
 
Unit_49_Class_1_Systems_Integration.pptx
bynehaijaz13
 
plant Photosynthesis and leaf structure.ppt
byEnas813292
 
LOWER LIMB ANATOMY notes for GROSS ANATOMY
bymarkmutugi44
 
UNIT I Stereoisomerism (Pharmaceutical Organic Chemistry III)
byssjsphs
 
Annual Report of CMC filed in the USFDA for NDA & ANDA
byPHARMA IQ EDUCATION
 
Aerobic-and-Anaerobic-Digesters-Biological-Waste-Treatment-Technologies.pptx
byShanmugaPriya168919
 
Basic Principles of Plant Pathology; Entomology & Nematology in Plant Patholo...
byNistarini College, Purulia (W.B) India
 
Bioremedation - Dechlorination ,Types and process , advantage and disadvantage
byswathijagadeesan1402
 
Betterszie | Exploring Dendrimer Generations Using the BeSEC
byBettersize Instruments
 
Light compensation point, CO2 compensation point, Quantum yield in plants.pptx
byRashmiMG2
 
PHYTOREMEDIATION OF HEAVY METALS IN SOIL
byswethaviji2005
 
Machine Learning Lectures --- Likelihood
byZahra Sadeghi
 
TOPIC - DROUGHT PRIMING AND STRESS MEMORY
byAbhishekkumawat67
 

Structure learning with Deep Autoencoders