Statistical inference of network structure
•
3 likes•596 views
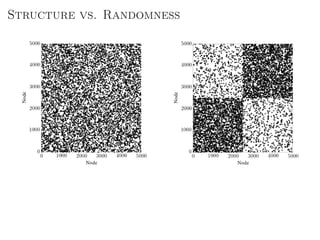
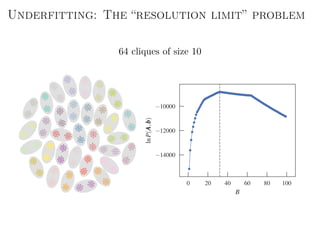
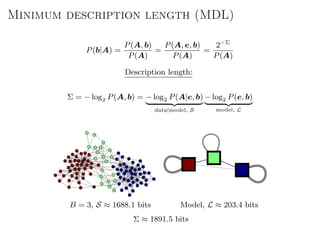
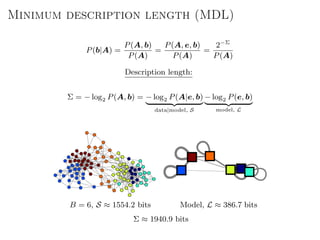
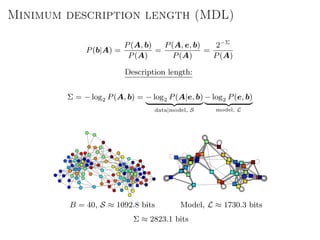
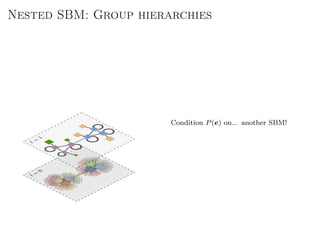
The document discusses Bayesian statistical inference for characterizing the structure of large networks. It introduces stochastic blockmodels as a generative model for network structure and describes performing Bayesian inference on these models. This involves defining a likelihood function based on a stochastic blockmodel, placing prior distributions on the model parameters, and computing the posterior distribution over partitions using Bayes' rule. Statistical inference provides a principled means of inferring community structure without overfitting and enables model selection among different partitions. Examples analyzing real networks demonstrate its ability to uncover meaningful structure.
Recommended
Recommended
More Related Content
Similar to Statistical inference of network structure
Similar to Statistical inference of network structure (20)
Recently uploaded
Recently uploaded (20)
Statistical inference of network structure
- 1. Statistical inference of network structure Tiago P. Peixoto University of Bath & ISI Foundation, Turin Salina, September 2017
- 2. Introductory text: “Bayesian stochastic blockmodeling”, arXiv: 1705.10225 For code, see: https://graph-tool.skewed.de (See also HOWTO at: https://graph-tool.skewed.de/ static/doc/demos/inference/inference.html) More infos at: https://skewed.de/tiago
- 3. How to characterize large-scale structures? (Flickr social network) (PGP web of trust) Find a meaningful network partition that provides: A division of nodes into groups that share similar properties. An understandable summary of the large-scale structure. An insight on function and evolution.
- 9. Structure vs. Randomness We need well defined, principled methodology, grounded on robust concepts of statistical inference.
- 10. Different methods, different results... Betweenness Modularity matrix Infomap Walk Trap Label propagation Modularity Modularity (Blondel) Spin glass Infomap (overlapping) Clique percolation
- 11. A principled alternative: Statistical inference What we have: A = {Aij} → Network What we want: b = {bi}, bi ∈ {1, . . . , B} → Partition into groups Generative model P(A|θ, b) → Model likelihood θ → Extra model parameters Bayesian posterior P(b|A) = P(A|b)P(b) P(A) (Bayes’ rule) P(A|b) = P(A|θ, b)P(θ|b) dθ (Marginal likelihood) P(θ, b) = P(θ|b)P(b) (Prior probability) P(A) = b P(A|b)P(b) (Evidence)
- 12. Why statistical inference? P(b|A) = P(A|b)P(b) P(A) (Bayes’ rule) P(A|b) = P(A|θ, b)P(θ|b) dθ Nonparametric Dimension of the model (i.e. number of groups B) can be inferred from data. Implements Occam’s razor and prevents overfitting. Model selection Different model classes, C1, C3, C3, . . . Posterior odds ratio: Λ = P(b1, C1|A) P(b2, C2|A) = P(A|b1, C1)P(b1)P(C1) P(A|b2, C2)P(b2)P(C2) If Λ > 1, (b1, C1) should be preferred over (b2, C2).
- 13. Overfitting, regularization and Occam’s razor P(θ|D) = P(D|θ)P(θ) P(D) D → Data, θ → Parameters Evidence: P(D) = P(D|θ)P(θ) dθ p(D) D D0 M1 M2 M3
- 14. Two approaches: Parametric vs. non-parametric Parametric P(b|A, θ) = P(A|b, θ)P(b) P(A|θ) θ → Remaining parameters are assumed to be known. Dimension of the model cannot be determined from data. Parameters θ are not typically known in practice. Problem has a simpler form, and becomes analytically tractable. Yields deeper understanding of the problem, and uncovers fundamental limits. Non-parametric P(b|A) = P(A|b)P(b) P(A) P(A|b) = P(A|θ, b)P(θ|b) dθ θ → Remaining parameters are unknown. Dimension of the model can be determined from data. Does not require knowledge of θ. Enables model selection, and prevents overfitting. Problem has a more complicated form, not amenable to the same tools used for the parametric case. (Our focus.)
- 15. The stochastic block model (SBM) Planted partition: N nodes divided into B groups (blocks). Parameters: bi → group membership of node i λrs → edge probability from group r to s. s r → Not restricted to assortative structures (“communities”). Easily generalizable (edge direction, overlapping groups, etc.)
- 16. Bayesian statistical inference Network probability: P(A|λ, b) A → Observed network λ, b → Model parameters s r b, λ −→ P (A|λ,b) A
- 17. Bayesian statistical inference Network probability: P(A|λ, b) A → Observed network λ, b → Model parameters A
- 18. Bayesian statistical inference Network probability: P(A|λ, b) A → Observed network λ, b → Model parameters A
- 19. Bayesian statistical inference Network probability: P(A|λ, b) A → Observed network λ, b → Model parameters ←− P (b|A) A
- 20. Bayesian statistical inference Network probability: P(A|λ, b) A → Observed network λ, b → Model parameters b ←− P (b|A) A
- 21. Bayesian statistical inference Network probability: P(A|λ, b) A → Observed network λ, b → Model parameters b ←− P (b|A) A P(b|A) = P(A|b)P(b) P(A) (Bayes’ rule) P(A|b) = P(A|λ, b)P(λ|b) dλ
- 22. The Poisson SBM Model likelihood: P(A|λ, b) = i<j λ Aij bibj e −λbibj Aij! × i (λbibi /2)Aii/2 e−λbibi /2 (Aii/2)!
- 23. The Poisson SBM Model likelihood: P(A|λ, b) = i<j λ Aij bibj e −λbibj Aij! × i (λbibi /2)Aii/2 e−λbibi /2 (Aii/2)! Noninformative prior for λ: P(λ|b) = r<s nrns ¯λ e−nrnsλrs/¯λ × r n2 r 2¯λ e−n2 rλrs/2¯λ
- 24. The Poisson SBM Model likelihood: P(A|λ, b) = i<j λ Aij bibj e −λbibj Aij! × i (λbibi /2)Aii/2 e−λbibi /2 (Aii/2)! Noninformative prior for λ: P(λ|b) = r<s nrns ¯λ e−nrnsλrs/¯λ × r n2 r 2¯λ e−n2 rλrs/2¯λ Marginal likelihood: P(A|b) = P(A|λ, b)P(λ|b) dλ = ¯λE (¯λ + 1)E+B(B+1)/2 × r<s ers! r err!! r ner r i<j Aij! i Aii!!
- 25. The Poisson SBM Model likelihood: P(A|λ, b) = i<j λ Aij bibj e −λbibj Aij! × i (λbibi /2)Aii/2 e−λbibi /2 (Aii/2)! Noninformative prior for λ: P(λ|b) = r<s nrns ¯λ e−nrnsλrs/¯λ × r n2 r 2¯λ e−n2 rλrs/2¯λ Marginal likelihood: P(A|b) = P(A|λ, b)P(λ|b) dλ = ¯λE (¯λ + 1)E+B(B+1)/2 × r<s ers! r err!! r ner r i<j Aij! i Aii!! Prior for b (tentative): P(b|B) = 1 BN P(B) = 1/N Posterior distribution: P(b|A) = P(A|b)P(b) P(A) P(A) = b P(A|b)P(b)
- 26. Example: American college football teams 1 5 10 15 20 25 30 B −2400 −2200 −2000 −1800 lnP(AAA,bbb) Original Randomized
- 27. Example: The Internet Movie Database (IMDB) Bipartite network of actors and films. Fairly large: N = 372, 787, E = 1, 812, 657
- 28. Example: The Internet Movie Database (IMDB) Bipartite network of actors and films. Fairly large: N = 372, 787, E = 1, 812, 657 MDL selects: B = 332
- 29. Example: The Internet Movie Database (IMDB) 135 223 72 317 32 253 63 182 46 302 66 232 133 246 8 178 116 320 161 175 53 292 14 216 6 278 12 213 108 301 156 195 128 233 50 222 104 211 146 256 162 166 119 239 21 206 115 190 154 313 155 326 38 286 152 319 89 238 9 281 49 293 93 269 153 227 23 237 57 289 151 179 71 276 19 173 137 308 60 330 69 248 42 297 134 1722 285 109 192 139 325 27 185 5 328 67 220 129 224 40 299 31 183 111 199 61 228 114 221 106 242 84 189 97 291 90 294 44 304 163 203 127 324 149 268 118 234 124 201 136 288 164 212 52 177 18 240 101 298 150 254 75 193 16 235 28 176 13 266 100 329 39 275 145 171 158 181 103 258 112 327 43 210 81 271 131 321 121 249 148 279 3 230 70 262 88 280 29 274 95 284 126 252 64 209 141 245 91 314 92 261 76 174 4 188 30 250 68 296 123 196 82 322 74 307 17 208 110 243 24 312 34 323 132 244 47 306 41 167 87 194 125 272 140 205 79 311 33 247 138 229 122 305 65 170 102 270 54 331 98 318 94 300 120 217 147 303 85 255 1 225 143 315 35 309 36 264 10 277 159 191 62 200 77 186 73 295 22 168 165 236 15 198 105 310 0 215 20 197 80 214 142 187 113 251 107 257 86 180 99 207 83 273 37 184 56 204 144 169 26 263 45 259 51 219 117287 58 290 160 202 11 316 48 282 7 267 96 231 25 265 157 260 78 226 130 283 55 241 59 218 Bipartite network of actors and films. Fairly large: N = 372, 787, E = 1, 812, 657 MDL selects: B = 332
- 30. Example: The Internet Movie Database (IMDB) 135 223 72 317 32 253 63 182 46 302 66 232 133 246 8 178 116 320 161 175 53 292 14 216 6 278 12 213 108 301 156 195 128 233 50 222 104 211 146 256 162 166 119 239 21 206 115 190 154 313 155 326 38 286 152 319 89 238 9 281 49 293 93 269 153 227 23 237 57 289 151 179 71 276 19 173 137 308 60 330 69 248 42 297 134 1722 285 109 192 139 325 27 185 5 328 67 220 129 224 40 299 31 183 111 199 61 228 114 221 106 242 84 189 97 291 90 294 44 304 163 203 127 324 149 268 118 234 124 201 136 288 164 212 52 177 18 240 101 298 150 254 75 193 16 235 28 176 13 266 100 329 39 275 145 171 158 181 103 258 112 327 43 210 81 271 131 321 121 249 148 279 3 230 70 262 88 280 29 274 95 284 126 252 64 209 141 245 91 314 92 261 76 174 4 188 30 250 68 296 123 196 82 322 74 307 17 208 110 243 24 312 34 323 132 244 47 306 41 167 87 194 125 272 140 205 79 311 33 247 138 229 122 305 65 170 102 270 54 331 98 318 94 300 120 217 147 303 85 255 1 225 143 315 35 309 36 264 10 277 159 191 62 200 77 186 73 295 22 168 165 236 15 198 105 310 0 215 20 197 80 214 142 187 113 251 107 257 86 180 99 207 83 273 37 184 56 204 144 169 26 263 45 259 51 219 117287 58 290 160 202 11 316 48 282 7 267 96 231 25 265 157 260 78 226 130 283 55 241 59 218 Bipartite network of actors and films. Fairly large: N = 372, 787, E = 1, 812, 657 MDL selects: B = 332 0 50 100 150 200 250 300 s 100 101 102 103 104 ers 103 nr 0 50 100 150 200 250 300 r 101 kr Bipartiteness is fully uncovered!
- 31. Example: The Internet Movie Database (IMDB) 135 223 72 317 32 253 63 182 46 302 66 232 133 246 8 178 116 320 161 175 53 292 14 216 6 278 12 213 108 301 156 195 128 233 50 222 104 211 146 256 162 166 119 239 21 206 115 190 154 313 155 326 38 286 152 319 89 238 9 281 49 293 93 269 153 227 23 237 57 289 151 179 71 276 19 173 137 308 60 330 69 248 42 297 134 1722 285 109 192 139 325 27 185 5 328 67 220 129 224 40 299 31 183 111 199 61 228 114 221 106 242 84 189 97 291 90 294 44 304 163 203 127 324 149 268 118 234 124 201 136 288 164 212 52 177 18 240 101 298 150 254 75 193 16 235 28 176 13 266 100 329 39 275 145 171 158 181 103 258 112 327 43 210 81 271 131 321 121 249 148 279 3 230 70 262 88 280 29 274 95 284 126 252 64 209 141 245 91 314 92 261 76 174 4 188 30 250 68 296 123 196 82 322 74 307 17 208 110 243 24 312 34 323 132 244 47 306 41 167 87 194 125 272 140 205 79 311 33 247 138 229 122 305 65 170 102 270 54 331 98 318 94 300 120 217 147 303 85 255 1 225 143 315 35 309 36 264 10 277 159 191 62 200 77 186 73 295 22 168 165 236 15 198 105 310 0 215 20 197 80 214 142 187 113 251 107 257 86 180 99 207 83 273 37 184 56 204 144 169 26 263 45 259 51 219 117287 58 290 160 202 11 316 48 282 7 267 96 231 25 265 157 260 78 226 130 283 55 241 59 218 Bipartite network of actors and films. Fairly large: N = 372, 787, E = 1, 812, 657 MDL selects: B = 332 0 50 100 150 200 250 300 s 100 101 102 103 104 ers 103 nr 0 50 100 150 200 250 300 r 101 kr Bipartiteness is fully uncovered! Meaningful features: Temporal Spatial (Country) Type/Genre
- 32. Example: The Internet Movie Database (IMDB) 135 223 72 317 32 253 63 182 46 302 66 232 133 246 8 178 116 320 161 175 53 292 14 216 6 278 12 213 108 301 156 195 128 233 50 222 104 211 146 256 162 166 119 239 21 206 115 190 154 313 155 326 38 286 152 319 89 238 9 281 49 293 93 269 153 227 23 237 57 289 151 179 71 276 19 173 137 308 60 330 69 248 42 297 134 1722 285 109 192 139 325 27 185 5 328 67 220 129 224 40 299 31 183 111 199 61 228 114 221 106 242 84 189 97 291 90 294 44 304 163 203 127 324 149 268 118 234 124 201 136 288 164 212 52 177 18 240 101 298 150 254 75 193 16 235 28 176 13 266 100 329 39 275 145 171 158 181 103 258 112 327 43 210 81 271 131 321 121 249 148 279 3 230 70 262 88 280 29 274 95 284 126 252 64 209 141 245 91 314 92 261 76 174 4 188 30 250 68 296 123 196 82 322 74 307 17 208 110 243 24 312 34 323 132 244 47 306 41 167 87 194 125 272 140 205 79 311 33 247 138 229 122 305 65 170 102 270 54 331 98 318 94 300 120 217 147 303 85 255 1 225 143 315 35 309 36 264 10 277 159 191 62 200 77 186 73 295 22 168 165 236 15 198 105 310 0 215 20 197 80 214 142 187 113 251 107 257 86 180 99 207 83 273 37 184 56 204 144 169 26 263 45 259 51 219 117287 58 290 160 202 11 316 48 282 7 267 96 231 25 265 157 260 78 226 130 283 55 241 59 218 Bipartite network of actors and films. Fairly large: N = 372, 787, E = 1, 812, 657 MDL selects: B = 332 0 50 100 150 200 250 300 s 100 101 102 103 104 ers 103 nr 0 50 100 150 200 250 300 r 101 kr Bipartiteness is fully uncovered! Meaningful features: Temporal Spatial (Country) Type/Genre
- 33. Example: The Internet Movie Database (IMDB) 135 223 72 317 32 253 63 182 46 302 66 232 133 246 8 178 116 320 161 175 53 292 14 216 6 278 12 213 108 301 156 195 128 233 50 222 104 211 146 256 162 166 119 239 21 206 115 190 154 313 155 326 38 286 152 319 89 238 9 281 49 293 93 269 153 227 23 237 57 289 151 179 71 276 19 173 137 308 60 330 69 248 42 297 134 1722 285 109 192 139 325 27 185 5 328 67 220 129 224 40 299 31 183 111 199 61 228 114 221 106 242 84 189 97 291 90 294 44 304 163 203 127 324 149 268 118 234 124 201 136 288 164 212 52 177 18 240 101 298 150 254 75 193 16 235 28 176 13 266 100 329 39 275 145 171 158 181 103 258 112 327 43 210 81 271 131 321 121 249 148 279 3 230 70 262 88 280 29 274 95 284 126 252 64 209 141 245 91 314 92 261 76 174 4 188 30 250 68 296 123 196 82 322 74 307 17 208 110 243 24 312 34 323 132 244 47 306 41 167 87 194 125 272 140 205 79 311 33 247 138 229 122 305 65 170 102 270 54 331 98 318 94 300 120 217 147 303 85 255 1 225 143 315 35 309 36 264 10 277 159 191 62 200 77 186 73 295 22 168 165 236 15 198 105 310 0 215 20 197 80 214 142 187 113 251 107 257 86 180 99 207 83 273 37 184 56 204 144 169 26 263 45 259 51 219 117287 58 290 160 202 11 316 48 282 7 267 96 231 25 265 157 260 78 226 130 283 55 241 59 218 Bipartite network of actors and films. Fairly large: N = 372, 787, E = 1, 812, 657 MDL selects: B = 332 0 50 100 150 200 250 300 s 100 101 102 103 104 ers 103 nr 0 50 100 150 200 250 300 r 101 kr Bipartiteness is fully uncovered! Meaningful features: Temporal Spatial (Country) Type/Genre
- 34. Example: The Internet Movie Database (IMDB) 135 223 72 317 32 253 63 182 46 302 66 232 133 246 8 178 116 320 161 175 53 292 14 216 6 278 12 213 108 301 156 195 128 233 50 222 104 211 146 256 162 166 119 239 21 206 115 190 154 313 155 326 38 286 152 319 89 238 9 281 49 293 93 269 153 227 23 237 57 289 151 179 71 276 19 173 137 308 60 330 69 248 42 297 134 1722 285 109 192 139 325 27 185 5 328 67 220 129 224 40 299 31 183 111 199 61 228 114 221 106 242 84 189 97 291 90 294 44 304 163 203 127 324 149 268 118 234 124 201 136 288 164 212 52 177 18 240 101 298 150 254 75 193 16 235 28 176 13 266 100 329 39 275 145 171 158 181 103 258 112 327 43 210 81 271 131 321 121 249 148 279 3 230 70 262 88 280 29 274 95 284 126 252 64 209 141 245 91 314 92 261 76 174 4 188 30 250 68 296 123 196 82 322 74 307 17 208 110 243 24 312 34 323 132 244 47 306 41 167 87 194 125 272 140 205 79 311 33 247 138 229 122 305 65 170 102 270 54 331 98 318 94 300 120 217 147 303 85 255 1 225 143 315 35 309 36 264 10 277 159 191 62 200 77 186 73 295 22 168 165 236 15 198 105 310 0 215 20 197 80 214 142 187 113 251 107 257 86 180 99 207 83 273 37 184 56 204 144 169 26 263 45 259 51 219 117287 58 290 160 202 11 316 48 282 7 267 96 231 25 265 157 260 78 226 130 283 55 241 59 218 Bipartite network of actors and films. Fairly large: N = 372, 787, E = 1, 812, 657 MDL selects: B = 332 0 50 100 150 200 250 300 s 100 101 102 103 104 ers 103 nr 0 50 100 150 200 250 300 r 101 kr Bipartiteness is fully uncovered! Meaningful features: Temporal Spatial (Country) Type/Genre
- 35. Example: The Internet Movie Database (IMDB) 135 223 72 317 32 253 63 182 46 302 66 232 133 246 8 178 116 320 161 175 53 292 14 216 6 278 12 213 108 301 156 195 128 233 50 222 104 211 146 256 162 166 119 239 21 206 115 190 154 313 155 326 38 286 152 319 89 238 9 281 49 293 93 269 153 227 23 237 57 289 151 179 71 276 19 173 137 308 60 330 69 248 42 297 134 1722 285 109 192 139 325 27 185 5 328 67 220 129 224 40 299 31 183 111 199 61 228 114 221 106 242 84 189 97 291 90 294 44 304 163 203 127 324 149 268 118 234 124 201 136 288 164 212 52 177 18 240 101 298 150 254 75 193 16 235 28 176 13 266 100 329 39 275 145 171 158 181 103 258 112 327 43 210 81 271 131 321 121 249 148 279 3 230 70 262 88 280 29 274 95 284 126 252 64 209 141 245 91 314 92 261 76 174 4 188 30 250 68 296 123 196 82 322 74 307 17 208 110 243 24 312 34 323 132 244 47 306 41 167 87 194 125 272 140 205 79 311 33 247 138 229 122 305 65 170 102 270 54 331 98 318 94 300 120 217 147 303 85 255 1 225 143 315 35 309 36 264 10 277 159 191 62 200 77 186 73 295 22 168 165 236 15 198 105 310 0 215 20 197 80 214 142 187 113 251 107 257 86 180 99 207 83 273 37 184 56 204 144 169 26 263 45 259 51 219 117287 58 290 160 202 11 316 48 282 7 267 96 231 25 265 157 260 78 226 130 283 55 241 59 218 Bipartite network of actors and films. Fairly large: N = 372, 787, E = 1, 812, 657 MDL selects: B = 332 0 50 100 150 200 250 300 s 100 101 102 103 104 ers 103 nr 0 50 100 150 200 250 300 r 101 kr Bipartiteness is fully uncovered! Meaningful features: Temporal Spatial (Country) Type/Genre
- 36. Example: The Internet Movie Database (IMDB) 135 223 72 317 32 253 63 182 46 302 66 232 133 246 8 178 116 320 161 175 53 292 14 216 6 278 12 213 108 301 156 195 128 233 50 222 104 211 146 256 162 166 119 239 21 206 115 190 154 313 155 326 38 286 152 319 89 238 9 281 49 293 93 269 153 227 23 237 57 289 151 179 71 276 19 173 137 308 60 330 69 248 42 297 134 1722 285 109 192 139 325 27 185 5 328 67 220 129 224 40 299 31 183 111 199 61 228 114 221 106 242 84 189 97 291 90 294 44 304 163 203 127 324 149 268 118 234 124 201 136 288 164 212 52 177 18 240 101 298 150 254 75 193 16 235 28 176 13 266 100 329 39 275 145 171 158 181 103 258 112 327 43 210 81 271 131 321 121 249 148 279 3 230 70 262 88 280 29 274 95 284 126 252 64 209 141 245 91 314 92 261 76 174 4 188 30 250 68 296 123 196 82 322 74 307 17 208 110 243 24 312 34 323 132 244 47 306 41 167 87 194 125 272 140 205 79 311 33 247 138 229 122 305 65 170 102 270 54 331 98 318 94 300 120 217 147 303 85 255 1 225 143 315 35 309 36 264 10 277 159 191 62 200 77 186 73 295 22 168 165 236 15 198 105 310 0 215 20 197 80 214 142 187 113 251 107 257 86 180 99 207 83 273 37 184 56 204 144 169 26 263 45 259 51 219 117287 58 290 160 202 11 316 48 282 7 267 96 231 25 265 157 260 78 226 130 283 55 241 59 218 Bipartite network of actors and films. Fairly large: N = 372, 787, E = 1, 812, 657 MDL selects: B = 332 0 50 100 150 200 250 300 s 100 101 102 103 104 ers 103 nr 0 50 100 150 200 250 300 r 101 kr Bipartiteness is fully uncovered! Meaningful features: Temporal Spatial (Country) Type/Genre
- 37. Example: The Internet Movie Database (IMDB) 135 223 72 317 32 253 63 182 46 302 66 232 133 246 8 178 116 320 161 175 53 292 14 216 6 278 12 213 108 301 156 195 128 233 50 222 104 211 146 256 162 166 119 239 21 206 115 190 154 313 155 326 38 286 152 319 89 238 9 281 49 293 93 269 153 227 23 237 57 289 151 179 71 276 19 173 137 308 60 330 69 248 42 297 134 1722 285 109 192 139 325 27 185 5 328 67 220 129 224 40 299 31 183 111 199 61 228 114 221 106 242 84 189 97 291 90 294 44 304 163 203 127 324 149 268 118 234 124 201 136 288 164 212 52 177 18 240 101 298 150 254 75 193 16 235 28 176 13 266 100 329 39 275 145 171 158 181 103 258 112 327 43 210 81 271 131 321 121 249 148 279 3 230 70 262 88 280 29 274 95 284 126 252 64 209 141 245 91 314 92 261 76 174 4 188 30 250 68 296 123 196 82 322 74 307 17 208 110 243 24 312 34 323 132 244 47 306 41 167 87 194 125 272 140 205 79 311 33 247 138 229 122 305 65 170 102 270 54 331 98 318 94 300 120 217 147 303 85 255 1 225 143 315 35 309 36 264 10 277 159 191 62 200 77 186 73 295 22 168 165 236 15 198 105 310 0 215 20 197 80 214 142 187 113 251 107 257 86 180 99 207 83 273 37 184 56 204 144 169 26 263 45 259 51 219 117287 58 290 160 202 11 316 48 282 7 267 96 231 25 265 157 260 78 226 130 283 55 241 59 218 Bipartite network of actors and films. Fairly large: N = 372, 787, E = 1, 812, 657 MDL selects: B = 332 0 50 100 150 200 250 300 s 100 101 102 103 104 ers 103 nr 0 50 100 150 200 250 300 r 101 kr Bipartiteness is fully uncovered! Meaningful features: Temporal Spatial (Country) Type/Genre
- 38. Underfitting: The “resolution limit” problem 64 cliques of size 10
- 39. Underfitting: The “resolution limit” problem 64 cliques of size 10 0 20 40 60 80 100 B −14000 −12000 −10000 lnP(AAA,bbb)
- 40. Underfitting: The “resolution limit” problem Remaining networkMerge candidates 100 101 102 103 104 105 N/B 101 102 103 104 ec Detectable Undetectable N = 103 N = 104 N = 105 N = 106 Minimum detectable block size ∼ √ N. Why?
- 41. Microcanonical equivalence Marginal likelihood: P(A|b) = P(A|λ, b)P(λ|b) dλ = ¯λE (¯λ + 1)E+B(B+1)/2 × r<s ers! r err!! r ner r i<j Aij! i Aii!!
- 42. Microcanonical equivalence Marginal likelihood: P(A|b) = P(A|λ, b)P(λ|b) dλ = ¯λE (¯λ + 1)E+B(B+1)/2 × r<s ers! r err!! r ner r i<j Aij! i Aii!! Equal to the joint probability of a microcanonical SBM: P(A|b) = P(A|e, b)P(e|b)
- 43. Microcanonical equivalence Marginal likelihood: P(A|b) = P(A|λ, b)P(λ|b) dλ = ¯λE (¯λ + 1)E+B(B+1)/2 × r<s ers! r err!! r ner r i<j Aij! i Aii!! Equal to the joint probability of a microcanonical SBM: P(A|b) = P(A|e, b)P(e|b) P(A|e, b) = r<s ers! r err!! r ner r i<j Aij! i Aii!! P(e|b) = r<s ¯λers (¯λ + 1)ers+1 r ¯λers/2 (¯λ + 1)ers/2+1
- 44. Microcanonical equivalence Marginal likelihood: P(A|b) = P(A|λ, b)P(λ|b) dλ = ¯λE (¯λ + 1)E+B(B+1)/2 × r<s ers! r err!! r ner r i<j Aij! i Aii!! Equal to the joint probability of a microcanonical SBM: P(A|b) = P(A|e, b)P(e|b) P(A|e, b) = r<s ers! r err!! r ner r i<j Aij! i Aii!! P(e|b) = r<s ¯λers (¯λ + 1)ers+1 r ¯λers/2 (¯λ + 1)ers/2+1 62 7 7 117 2 1 46 2 60 Edge counts, e Network, A
- 45. Minimum description length (MDL) P(b|A) = P(A, b) P(A) = P(A, e, b) P(A) = 2−Σ P(A) Description length: Σ = − log2 P(A, b) = − log2 P(A|e, b) data|model, S − log2 P(e, b) model, L
- 46. Minimum description length (MDL) P(b|A) = P(A, b) P(A) = P(A, e, b) P(A) = 2−Σ P(A) Description length: Σ = − log2 P(A, b) = − log2 P(A|e, b) data|model, S − log2 P(e, b) model, L B = 2, S ≈ 1805.3 bits Model, L ≈ 122.6 bits Σ ≈ 1927.9 bits
- 47. Minimum description length (MDL) P(b|A) = P(A, b) P(A) = P(A, e, b) P(A) = 2−Σ P(A) Description length: Σ = − log2 P(A, b) = − log2 P(A|e, b) data|model, S − log2 P(e, b) model, L B = 3, S ≈ 1688.1 bits Model, L ≈ 203.4 bits Σ ≈ 1891.5 bits
- 48. Minimum description length (MDL) P(b|A) = P(A, b) P(A) = P(A, e, b) P(A) = 2−Σ P(A) Description length: Σ = − log2 P(A, b) = − log2 P(A|e, b) data|model, S − log2 P(e, b) model, L B = 4, S ≈ 1640.8 bits Model, L ≈ 270.7 bits Σ ≈ 1911.5 bits
- 49. Minimum description length (MDL) P(b|A) = P(A, b) P(A) = P(A, e, b) P(A) = 2−Σ P(A) Description length: Σ = − log2 P(A, b) = − log2 P(A|e, b) data|model, S − log2 P(e, b) model, L B = 5, S ≈ 1590.5 bits Model, L ≈ 330.8 bits Σ ≈ 1921.3 bits
- 50. Minimum description length (MDL) P(b|A) = P(A, b) P(A) = P(A, e, b) P(A) = 2−Σ P(A) Description length: Σ = − log2 P(A, b) = − log2 P(A|e, b) data|model, S − log2 P(e, b) model, L B = 6, S ≈ 1554.2 bits Model, L ≈ 386.7 bits Σ ≈ 1940.9 bits
- 51. Minimum description length (MDL) P(b|A) = P(A, b) P(A) = P(A, e, b) P(A) = 2−Σ P(A) Description length: Σ = − log2 P(A, b) = − log2 P(A|e, b) data|model, S − log2 P(e, b) model, L B = 10, S ≈ 1451.0 bits Model, L ≈ 590.8 bits Σ ≈ 2041.8 bits
- 52. Minimum description length (MDL) P(b|A) = P(A, b) P(A) = P(A, e, b) P(A) = 2−Σ P(A) Description length: Σ = − log2 P(A, b) = − log2 P(A|e, b) data|model, S − log2 P(e, b) model, L B = 20, S ≈ 1300.7 bits Model, L ≈ 1037.8 bits Σ ≈ 2338.6 bits
- 53. Minimum description length (MDL) P(b|A) = P(A, b) P(A) = P(A, e, b) P(A) = 2−Σ P(A) Description length: Σ = − log2 P(A, b) = − log2 P(A|e, b) data|model, S − log2 P(e, b) model, L B = 40, S ≈ 1092.8 bits Model, L ≈ 1730.3 bits Σ ≈ 2823.1 bits
- 54. Minimum description length (MDL) P(b|A) = P(A, b) P(A) = P(A, e, b) P(A) = 2−Σ P(A) Description length: Σ = − log2 P(A, b) = − log2 P(A|e, b) data|model, S − log2 P(e, b) model, L B = 70, S ≈ 881.3 bits Model, L ≈ 2427.3 bits Σ ≈ 3308.6 bits
- 55. Minimum description length (MDL) P(b|A) = P(A, b) P(A) = P(A, e, b) P(A) = 2−Σ P(A) Description length: Σ = − log2 P(A, b) = − log2 P(A|e, b) data|model, S − log2 P(e, b) model, L B = N, S = 0 bits Model, L ≈ 3714.9 bits Σ ≈ 3714.9 bits
- 56. Minimum description length (MDL) P(b|A) = P(A, b) P(A) = P(A, e, b) P(A) = 2−Σ P(A) Description length: Σ = − log2 P(A, b) = − log2 P(A|e, b) data|model, S − log2 P(e, b) model, L B = 3, S ≈ 1688.1 bits Model, L ≈ 203.4 bits Σ ≈ 1891.5 bits
- 57. Noninformative priors and underfitting Σ ≈ −(E − N) log2 B + B(B + 1) 2 log2 E
- 58. Noninformative priors and underfitting Σ ≈ −(E − N) log2 B + B(B + 1) 2 log2 E Bmax ∝ √ N “resolution limit”
- 59. Noninformative priors and underfitting Σ ≈ −(E − N) log2 B + B(B + 1) 2 log2 E Bmax ∝ √ N “resolution limit” Q: How to do better without prior information?
- 60. Noninformative priors and underfitting Σ ≈ −(E − N) log2 B + B(B + 1) 2 log2 E Bmax ∝ √ N “resolution limit” Q: How to do better without prior information? A: Construct a model for the model! P(A|b) = P(A|λ, b)P(λ|φ)P(φ) dλ dφ
- 61. Noninformative priors and underfitting Σ ≈ −(E − N) log2 B + B(B + 1) 2 log2 E Bmax ∝ √ N “resolution limit” Q: How to do better without prior information? A: Construct a model for the model! P(A|b) = P(A|λ, b)P(λ|φ)P(φ) dλ dφ Microcanonical: P(A|b) = P(A|e, b)P(e|ψ)P(ψ)
- 62. Prior for the partition
- 63. Prior for the partition Option 1: Noninformative P(b) = 1 N B=1 N B B!
- 64. Prior for the partition Option 1: Noninformative P(b) = 1 N B=1 N B B! Option 2: Slightly less noninformative P(b|B) = 1 N B B! P(B) = 1 N
- 65. Prior for the partition Option 1: Noninformative P(b) = 1 N B=1 N B B! Option 2: Slightly less noninformative P(b|B) = 1 N B B! P(B) = 1 N Option 3: Conditioned on group sizes P(b|B) = P(b|n)P(n) = N! r nr! × N − 1 B − 1 −1
- 66. Prior for the partition Option 1: Noninformative P(b) = 1 N B=1 N B B! Option 2: Slightly less noninformative P(b|B) = 1 N B B! P(B) = 1 N Option 3: Conditioned on group sizes P(b|B) = P(b|n)P(n) = N! r nr! × N − 1 B − 1 −1 For N B: − ln P(b|B) ≈ NH(n) + O(B ln N) H(n) = − r nr N ln nr N
- 67. Prior for the edge counts 62 7 7 1 17 2 1 46 2 60 Option 1: Noninformative P(e) = B 2 E −1 n m = n+m−1 m
- 68. Nested SBM: Group hierarchies l = 0 Condition P(e) on... another SBM!
- 69. Nested SBM: Group hierarchies l = 0 l = 1 Condition P(e) on... another SBM!
- 70. Nested SBM: Group hierarchies l = 0 l = 1 l = 2 Condition P(e) on... another SBM!
- 71. Nested SBM: Group hierarchies l = 0 l = 1 l = 2 l = 3 Condition P(e) on... another SBM!
- 72. Nested SBM: Group hierarchies l = 0 l = 1 l = 2 l = 3 NestedmodelObservednetwork N nodes E edges B0 nodes E edges B1 nodes E edges B2 nodes E edges Condition P(e) on... another SBM!
- 73. Nested SBM: Group hierarchies l = 0 l = 1 l = 2 l = 3 NestedmodelObservednetwork N nodes E edges B0 nodes E edges B1 nodes E edges B2 nodes E edges Condition P(e) on... another SBM!
- 74. Nested SBM: Group hierarchies l = 0 l = 1 l = 2 l = 3 NestedmodelObservednetwork N nodes E edges B0 nodes E edges B1 nodes E edges B2 nodes E edges Condition P(e) on... another SBM! 100 101 102 103 104 105 N/B 101 102 103 104 ec Detectable Detectable with nested model Undetectable N = 103 N = 104 N = 105 N = 106 For planted partition: Bmax = O N log N √ N
- 75. Nested SBM prevents underfitting 64 cliques of size 10 0 20 40 60 80 100 B 6000 8000 10000 12000 14000 16000 Σ=−log2P(AAA,bbb)(bits) SBM Nested SBM
- 76. Resolution problem in the wild Noninformative Hierarchical 102 103 104 105 106 107 E 101 102 103 104 N/B 0 1 2 3 4 5 6 7 8 9 10 11 12 1314 1516 17 18 19 20 21 2223 24 25 26 272829 30 31 32 102 103 104 105 106 107 E 101 102 103 104 N/B 0 1 2 3 4 5 6 7 8 9 1011 121314 1516 17 18 1920 21 2223 24 25 26 27 2829 30 31 32
- 77. Hierarchical model: Built-in validation 0.5 0.6 0.7 0.8 0.9 1.0 c 0.0 0.2 0.4 0.6 0.8 1.0 NMI 1 2 3 4 5 L (a) (b) (c) (d) NMI (B=16) NMI (nested) Inferred L (a) (b) (c) (d)
- 78. Nested SBM: Modeling at multiple scales Internet (AS) (N = 52, 104, E = 399, 625)
- 79. Nested SBM: Modeling at multiple scales IMDB Film-Actor Network (N = 372, 447, E = 1, 812, 312, B = 717)
- 80. Nested SBM: Modeling at multiple scales Human connectome
- 82. Degree-correction Traditional SBM Degree-corrected SBM P(A|λ, θ, b) = i<j (θiθjλbibj )Aij e −θiθj λbibj Aij! × i (θ2 i λbibi /2)Aii/2 e−θ2 i λbibi /2 (Aii/2)! θi → average degree of node i (Karrer and Newman 2011)
- 83. Degree-correction Traditional SBM Degree-corrected SBM P(A|λ, θ, b) = i<j (θiθjλbibj )Aij e −θiθj λbibj Aij! × i (θ2 i λbibi /2)Aii/2 e−θ2 i λbibi /2 (Aii/2)! θi → average degree of node i (Karrer and Newman 2011)
- 84. Degree-corrected microcanonical SBM Noninformative priors: P(λ|b) = r≤s e−λrs/(1+δrs)¯λ /(1 + δrs)¯λ P(θ|b) = r (nr − 1)!δ( i θiδbi,r − 1)
- 85. Degree-corrected microcanonical SBM Noninformative priors: P(λ|b) = r≤s e−λrs/(1+δrs)¯λ /(1 + δrs)¯λ P(θ|b) = r (nr − 1)!δ( i θiδbi,r − 1) Marginal likelihood: P(A|b) = P(A|λ, θ, b)P(λ|b)P(θ|b) dλdθ = ¯λE (¯λ + 1)E+B(B+1)/2 × r<s ers! r err!! i<j Aij! i Aii!! × r (nr − 1)! (er + nr − 1)! × i ki!
- 86. Degree-corrected microcanonical SBM Noninformative priors: P(λ|b) = r≤s e−λrs/(1+δrs)¯λ /(1 + δrs)¯λ P(θ|b) = r (nr − 1)!δ( i θiδbi,r − 1) Marginal likelihood: P(A|b) = P(A|λ, θ, b)P(λ|b)P(θ|b) dλdθ = ¯λE (¯λ + 1)E+B(B+1)/2 × r<s ers! r err!! i<j Aij! i Aii!! × r (nr − 1)! (er + nr − 1)! × i ki! Microcanonical equivalence: P(A|b) = P(A|k, e, b)P(k|e, b)P(e) P(A|k, e, b) = r<s ers! r err!! i ki! i<j Aij! i Aii!! r er!! P(k|e, b) = r nr er −1 Edge counts e. Degrees, k. Network, A.
- 87. Prior for the degrees Option 0: Random half-edges (Non-degree-corrected) P(k|e, b) = r er! ner r i∈r ki! 0 20 40 60 80 100 k 10−1 100 101 102 103 ηk
- 88. Prior for the degrees Option 0: Random half-edges (Non-degree-corrected) P(k|e, b) = r er! ner r i∈r ki! Option 1: Noninformative P(k|e, b) = r nr er −1 0 20 40 60 80 100 k 10−1 100 101 102 103 ηk Non-degree-corrected Noninformative
- 89. Prior for the degrees Option 2: Conditioned on degree distribution P(k|b, e) = P(k|η)P(η) = r nr! r ηr k! × r q(er, nr)−1
- 90. Prior for the degrees Option 2: Conditioned on degree distribution P(k|b, e) = P(k|η)P(η) = r nr! r ηr k! × r q(er, nr)−1 0 500 1000 1500 2000 k 10−3 10−2 10−1 100 101 102 103 104 ηk Non-degree-corrected Uniform Conditioned on uniform hyperprior 100 101 102 103 104 10−5 10−4 10−3 10−2 10−1 100 101 102 103 104
- 91. Prior for the degrees Option 2: Conditioned on degree distribution P(k|b, e) = P(k|η)P(η) = r nr! r ηr k! × r q(er, nr)−1 0 500 1000 1500 2000 k 10−3 10−2 10−1 100 101 102 103 104 ηk Non-degree-corrected Uniform Conditioned on uniform hyperprior 100 101 102 103 104 10−5 10−4 10−3 10−2 10−1 100 101 102 103 104 Bose-Einstein statistics N “bosons” (nodes) ki → “energy level” (degree) ηk ≈ 1 exp k ζ(2)/E − 1 . ηk ≈ E/ζ(2)/k for k √ E, exp(−k ζ(2)/E) for k √ E.
- 92. Prior for the degrees Option 2: Conditioned on degree distribution P(k|b, e) = P(k|η)P(η) = r nr! r ηr k! × r q(er, nr)−1 0 500 1000 1500 2000 k 10−3 10−2 10−1 100 101 102 103 104 ηk Non-degree-corrected Uniform Conditioned on uniform hyperprior 100 101 102 103 104 10−5 10−4 10−3 10−2 10−1 100 101 102 103 104 Bose-Einstein statistics N “bosons” (nodes) ki → “energy level” (degree) ηk ≈ 1 exp k ζ(2)/E − 1 . ηk ≈ E/ζ(2)/k for k √ E, exp(−k ζ(2)/E) for k √ E. − ln P(k|e, b) ≈ r nrH(ηr) + O( √ nr) H(ηr) = − k (ηr k/nr) ln(ηr k/nr)
- 93. Prior for the degrees: Integer partitions q(m, n) → number of partitions of integer m into at most n parts Exact computation q(m, n) = q(m, n − 1) + q(m − n, n) Full table for n ≤ m ≤ M in time O(M2 ).
- 94. Prior for the degrees: Integer partitions q(m, n) → number of partitions of integer m into at most n parts Exact computation q(m, n) = q(m, n − 1) + q(m − n, n) Full table for n ≤ m ≤ M in time O(M2 ). Approximation q(m, n) ≈ f(u) m exp( √ mg(u)), u = n/ √ m f(u) = v(u) 23/2πu 1 − (1 + u2 /2)e−v(u) −1/2 g(u) = 2v(u) u − u ln(1 − e−v(u) ) v = u −v2/2 − Li2(1 − ev) (Szekeres, 1951)
- 95. Prior for the degrees: Integer partitions q(m, n) → number of partitions of integer m into at most n parts Exact computation q(m, n) = q(m, n − 1) + q(m − n, n) Full table for n ≤ m ≤ M in time O(M2 ). 0 2000 4000 6000 8000 10000 m 0 50 100 150 200 250 lnq(m,n) n = 10000 n = 100 n = 30 n = 10 n = 2 Exact Approximation Approximation q(m, n) ≈ f(u) m exp( √ mg(u)), u = n/ √ m f(u) = v(u) 23/2πu 1 − (1 + u2 /2)e−v(u) −1/2 g(u) = 2v(u) u − u ln(1 − e−v(u) ) v = u −v2/2 − Li2(1 − ev) (Szekeres, 1951)
- 96. Example: Political blogs redux N = 1, 222, E = 19, 027 (a) NDC-SBM, B1 = 42, Σ ≈ 89938 bits (b) DC-SBM, uniform prior, B1 = 23, Σ ≈ 87162 bits (c) DC-SBM, uniform hyperprior, B1 = 20, Σ ≈ 84890 bits
- 97. Model selection Λ = P(A, {bl}|C1)P(C1) P(A, {bl}|C2)P(C2) = 2−∆Σ
- 98. Model selection Λ = P(A, {bl}|C1)P(C1) P(A, {bl}|C2)P(C2) = 2−∆Σ Southern w om en interactions Zachary’skarateclub D olphin socialnetw ork Charactersin LesM is´erables A m erican collegefootball Floridafood w eb (w et) Residencehallfriendships C.elegansneuralnetw ork Scientificcoauthorships Country-languagenetw ork M alariagenesim ilarityE-m ail Politicalblogs Scientificcoauthorships Protein interactions(I) Biblenam esco-ocurrence G lobalairportnetw ork W estern statespow ergrid Protein interactions(II) InternetA S A dvogato usertrust Chessgam es D ictionary entries Coracitations G oogle+ socialnetw ork arX iv hep-th citations Linux sourcedependency PG P w eb oftrust Facebook w allposts Brightkitesocialnetw ork G nutellahosts Youtubegroup m em berships −105 −104 −103 −102 −101 −100 0 log10Λ1 DC-SBM, uniform hyperprior DC-SBM, uniform prior NDC-SBM
- 99. Inferring group assignments: Sampling vs. Maximization ˆb → estimator, b∗ → true partition Maximum a posteriori (MAP) Indicator loss function: ∆(ˆb, b∗ ) = i δˆbi,b∗ i Maximization over the posterior b ∆(ˆb, b)P(b|A) yields the MAP estimator ˆb = argmax b P(b|A). (Identical to MDL.) Node marginals Overlap loss function: d(ˆb, b∗ ) = 1 N i δˆbi,b∗ i Maximization over the posterior b d(ˆb, b)P(b|A) yields the marginal estimator ˆbi = argmax r πi(r), πi(r) = bbi P(bi = r, b bi|A).
- 100. Sampling vs. maximization Zachary’s karate club (a) b0, Σ = 321.3 bits (b) b1, Σ = 327.5 bits (c) b2, Σ = 329.3 bits Partition space Partition space −Σ=log2P(AAA,bbb) −355 −350 −345 −340 −335 −330 −325 bbb2bbb1 bbb0 (d) 1 2 3 4 5 B 0.0 0.1 0.2 0.3 0.4 0.5 P(B|AAA) (e)
- 101. Sampling vs. Maximization Bias-variance trade-off Maximization (MDL) {ˆbl} = argmax {bl} P({bl}|A) Finds the best partition, and number of groups {Bl}. Lower variance, higher bias Tendency to underfit. Sampling {bl} ∼ P({bl}|A) Finds the best posterior ensemble; marginal posterior P(Bl|A). Higher variance, lower bias Tendency to overfit.
- 102. Sampling vs. maximization Collaborations between scientists (N = 1, 589, E = 2, 742) (a) (b) 40 45 50 55 60 65 70 75 80 85 90 B1 0.00 0.02 0.04 0.06 0.08 0.10 0.12 0.14 0.16 0.18 P(B1|AAA) DC-SBM, uniform hyperprior DC-SBM, uniform prior NDC-SBM 12 15 18 21 24 27 30 33 36 B2 0.00 0.05 0.10 0.15 0.20 0.25 0.30 P(B2|AAA) 4 8 12 16 20 B3 0.00 0.05 0.10 0.15 0.20 0.25 0.30 0.35 0.40 P(B3|AAA)
- 103. Inference algorithm: Metropolis-Hastings Move proposal, bi = r → bi = s Accept with probability a = min 1, P(b |A)P(b → b ) P(b|A)P(b → b) . Move proposal of node i requires O(ki) operations. A whole MCMC sweep can be performed in O(E) time, independent of the number of groups, B. In contrast to: 1. EM + BP with Bernoulli SBM: O(EB2 ) (Semiparametric) [Decelle et al, 2011] 2. Variational Bayes with (overlapping) Bernoulli SBM: O(EB) (Semiparametric) [Gopalan and Blei, 2011] 3. Bernoulli SBM with noninformative priors: O(EB2 ) (Greedy) [Cˆome and Latouche, 2015] 4. Poisson SBM with noninformative priors: O(EB2 ) (heat bath) [Newman and Reinert, 2016]
- 104. Efficient inference: other improvements Smart move proposals Choose a random vertex i (happens to belong to group r). Move it to a random group s ∈ [1, B], chosen with a probability p(r → s|t) proportional to ets + , where t is the group membership of a randomly chosen neighbour of i. i bi = r j bj = t etr ets etur t s u Fast mixing times. Agglomerative initialization Start with B = N. Progressively merge groups. Avoids metastable states.
- 105. Efficient inference: other improvements 100 101 102 103 104 τ + 1 (sweeps) 0.0 0.2 0.4 0.6 0.8 1.0 R(τ) = 0.01 → ∞ 0 200 400 600 800 1000 1200 MCMC Sweeps −1.2 −1.0 −0.8 −0.6 −0.4 −0.2 0.0 St Greedy heuristic: P(b|A)β , β → ∞
- 106. Fundamental limits on community detection Bayes-optimal case, with known parameters: γ, λ Partition prior: P(b|γ) = i γbi . Parametric posterior: P(b|A, λ, γ) = P(A|b, λ)P(b|γ) P(A|λ, γ) = e−H(b) Z Potts-like Hamiltonian: H(b) = − i<j (Aij ln λbi,bj − λbi,bj ) − i ln γbi , Partition function: Z = b e−H(b) Aurelien Decelle, Florent Krzakala, Cristopher Moore, and Lenka Zdeborov´a, PRL 107, 065701 (2011).
- 107. Fundamental limits on community detection If A is a tree: F = − ln Z = − i ln Zi + i<j Aij ln Zij − E with the auxiliary quantities given by Zij = N r<s λrs(ψi→j r ψj→i s + ψi→j s ψj→i r ) + N r λrrψi→j r ψj→i r Zi = r nre−hr j∈∂i r Nλrbi ψj→i r , ψi→j r → “messages”, obeying the Belief Propagation (BP) equations: ψi→j r = 1 Zi→j γre−hr k∈∂ij s Nλrsψk→i s → O(NB2 ) Marginal distribution: P(bi = r|A, λ, γ) = ψi r = 1 Zi γr j∈∂i s (Nλrs)Aij e−λrs ψj→i s SBM graphs are asymptotically tree-like! Aurelien Decelle, Florent Krzakala, Cristopher Moore, and Lenka Zdeborov´a, PRL 107, 065701 (2011).
- 108. Fundamental limits on community detection Planted partition: λrs = λinδrs + λout(1 − δrs) = N(λin − λout) 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 overlap ε= cout/cin undetectabledetectable q=2, c=3 εs overlap, N=500k, BP overlap, N=70k, MC 0 0.2 0.4 0.6 0.8 1 0 0.2 0.4 0.6 0.8 1 0 100 200 300 400 500 iterations ε= cout/cin εs undetectabledetectable q=4, c=16 overlap, N=100k, BP overlap, N=70k, MC iterations, N=10k iterations, N=100k 0 0.2 0.4 0.6 0.8 1 12 13 14 15 16 17 18 0 0.1 0.2 0.3 0.4 0.5 fpara-forder c undetect. hard detect. easy detect. q=5,cin=0, N=100k cd cc cs init. ordered init. random fpara-forder Detectability transition: ∗ = B k (Algorithmic independent!) Rigorously proven: e.g. E. Mossel, J. Neeman, and A. Sly (2015).; E. Mossel, J. Neeman, and A. Sly (2014); C. Bordenave, M. Lelarge, and L. Massouli´e, (2015) Aurelien Decelle, Florent Krzakala, Cristopher Moore, and Lenka Zdeborov´a, PRL 107, 065701 (2011).
- 109. Prediction of missing edges A = AO Observed ∪ δA Missing Posterior probability of missing edges P(δA|AO ) ∝ b PG(AO ∪ δA|b) PG(AO|b) PG(b|AO ) A. Clauset, C. Moore, MEJ Newman, Nature, 2008 R. Guimer`a, M Sales-Pardo, PNAS 2009 Drug-drug interactions R. Guimer`a, M. Sales-Pardo, PLoS Comput Biol, 2013
- 110. Weighted graphs Adjacency: Aij ∈ {0, 1} or N Weights: xij ∈ N or R SBMs with edge covariates: P(A, x|θ, γ, b) = P(x|A, γ, b)P(A|θ, b) Adjacency: P(A|θ = {λ, κ}, b) = i<j e−λbi,bj κiκj (λbi,bjκiκj)Aij Aij! , Edge covariates: P(x|A, γ, b) = r≤s P(xrs|γrs) P(x|γ) → Exponential, Normal, Geometric, Binomial, Poisson, . . . C. Aicher et al. Journal of Complex Networks 3(2), 221-248 (2015); T.P.P arXiv: 1708.01432
- 111. Weighted graphs T.P.P arXiv: 1708.01432 Nonparametric Bayesian approach P(b|A, x) = P(A, x|b)P(b) P(A, x) , Marginal likelihood: P(A, x|b) = P(A, x|θ, γ, b)P(θ)P(γ) dθdγ = P(A|b)P(x|A, b), Adjacency part (unweighted): P(A|b) = P(A|θ, b)P(θ) dθ Weights part: P(x|A, b) = P(x|A, γ, b)P(γ) dγ = r≤s P(xrs|γrs)P(γrs) dγrs
- 112. UN Migrations
- 113. UN Migrations 100 101 102 103 104 105 106 Migrations 10−9 10−8 10−7 10−6 10−5 10−4 10−3 10−2 10−1 Probability SBM fit with geometric weights Geometric distribution fit
- 114. Votes in congress Deputy Deputy 0.0 0.2 0.4 0.6 0.8 Votecorrelation Opposit ion Gove rnment −0.2 0.0 0.2 0.4 0.6 0.8 1.0 Vote correlation 0 1 2 3 4 Probabilitydensity SBM fit on original data SBM fit on shuffled data
- 115. Human connectome Right hemisphere Left hemisphere 10−1 100 101 102 Electrical connectivity (mm−1) 10−8 10−6 10−4 10−2 100 Probabilitydensity SBM fit 0.1 0.2 0.3 0.4 0.5 0.6 Fractional anisotropy (dimensionless) 0 1 2 3 4 5 Probabilitydensity SBM fit
- 116. Overlapping groups c) (Palla et al 2005)
- 117. Overlapping groups c) (Palla et al 2005)
- 118. Overlapping groups c) (Palla et al 2005) Number of nonoverlapping partitions: BN Number of overlapping partitions: 2BN
- 119. Overlapping groups c) (Palla et al 2005) Number of nonoverlapping partitions: BN Number of overlapping partitions: 2BN
- 120. Group overlap P(A|κ, λ) = i<j e−λij λ Aij ij Aij! × i e−λii/2 (λii/2)Aii/2 Aii/2! , λij = rs κirλrsκjs Labelled half-edges: Aij = rs Grs ij , P(A|κ, λ) = G P(G|κ, λ)
- 121. Group overlap P(A|κ, λ) = i<j e−λij λ Aij ij Aij! × i e−λii/2 (λii/2)Aii/2 Aii/2! , λij = rs κirλrsκjs Labelled half-edges: Aij = rs Grs ij , P(A|κ, λ) = G P(G|κ, λ) P(G) = P(G|κ, λ)P(κ)P(λ|¯λ) dκdλ, = ¯λE (¯λ + 1)E+B(B+1)/2 r<s ers! r err!! rs i<j Grs ij ! i Grs ii !! × r (N − 1)! (er + N − 1)! × ir kr i !,
- 122. Group overlap P(A|κ, λ) = i<j e−λij λ Aij ij Aij! × i e−λii/2 (λii/2)Aii/2 Aii/2! , λij = rs κirλrsκjs Labelled half-edges: Aij = rs Grs ij , P(A|κ, λ) = G P(G|κ, λ) P(G) = P(G|κ, λ)P(κ)P(λ|¯λ) dκdλ, = ¯λE (¯λ + 1)E+B(B+1)/2 r<s ers! r err!! rs i<j Grs ij ! i Grs ii !! × r (N − 1)! (er + N − 1)! × ir kr i !, Microcanonical equivalence: P(G) = P(G|k, e)P(k|e)P(e), P(G|k, e) = r<s ers! r err!! ir kr i ! rs i<j Grs ij ! i Grs ii !! r er! , P(k|e) = r er N −1
- 123. Overlap vs. non-overlap Social “ego” network (from Facebook) 0 8 16 24 k 0 1 2 3 4 nk 0 5 10 15 20 k 0 2 4 6 nk 3 6 9 k 0 1 2 3 nk 4 8 12 16 k 0 1 2 3 nk B = 4, Λ 0.053
- 124. Overlap vs. non-overlap Social “ego” network (from Facebook) 0 8 16 24 k 0 1 2 3 4 nk 0 5 10 15 20 k 0 2 4 6 nk 3 6 9 k 0 1 2 3 nk 4 8 12 16 k 0 1 2 3 nk 0 8 16 24 k 0 1 2 3 4 nk 0 3 6 k 0 2 4 nk 0 3 6 9 k 0 1 2 3nk 4 8 12 k 0 1 2 3 nk B = 4, Λ 0.053 B = 5, Λ = 1
- 125. Overlap vs. non-overlap 0.0 0.2 0.4 0.6 0.8 1.0 µ 4.5 5.0 5.5 6.0 Σ/E B = 4 (overlapping) B = 15 (nonoverlapping)
- 126. SBM with layers T.P.P, Phys. Rev. E 92, 042807 (2015) C o lla p sed l = 1 l = 2 l = 3 Fairly straightforward. Easily combined with degree-correction, overlaps, etc. Edge probabilities are in general different in each layer. Node memberships can move or stay the same across layer. Works as a general model for discrete as well as discretized edge covariates. Works as a model for temporal networks.
- 127. SBM with layers Edge covariates P({Al}|{θ}) = P(Ac|{θ}) r≤s l ml rs! mrs! Independent layers P({Al}|{{θ}l}, {φ}, {zil}}) = l P(Al|{θ}l, {φ}) Embedded models can be of any type: Traditional, degree-corrected, overlapping.
- 128. Layer information can reveal hidden structure
- 129. Layer information can reveal hidden structure
- 130. ... but it can also hide structure! → · · · × C 0.0 0.2 0.4 0.6 0.8 1.0 c 0.0 0.2 0.4 0.6 0.8 1.0 NMI Collapsed E/C = 500 E/C = 100 E/C = 40 E/C = 20 E/C = 15 E/C = 12 E/C = 10 E/C = 5
- 131. Model selection Null model: Collapsed (aggregated) SBM + fully random layers P({Gl}|{θ}, {El}) = P(Gc|{θ}) × l El! E! (we can also aggregate layers into larger layers)
- 132. Model selection Example: Social network of physicians N = 241 Physicians Survey questions: “When you need information or advice about questions of therapy where do you usually turn?” “And who are the three or four physicians with whom you most often find yourself discussing cases or therapy in the course of an ordinary week – last week for instance?” “Would you tell me the first names of your three friends whom you see most often socially?” T.P.P, Phys. Rev. E 92, 042807 (2015)
- 133. Model selection Example: Social network of physicians
- 134. Model selection Example: Social network of physicians
- 135. Model selection Example: Social network of physicians Λ = 1 log10 Λ ≈ −50
- 136. Example: Brazilian chamber of deputies Voting network between members of congress (1999-2006) PMDB, PP, PT B DEM,PP PT PP,PMDB,PTB PDT ,PSB,PCdoBPTB,PMDBPSDB,PR DEM ,PFLPSDB PT PP,PTB Right Center Left
- 137. Example: Brazilian chamber of deputies Voting network between members of congress (1999-2006) PMDB, PP, PT B DEM,PP PT PP,PMDB,PTB PDT ,PSB,PCdoBPTB,PMDBPSDB,PR DEM ,PFLPSDB PT PP,PTB Right Center Left PR,PFL,PM D B PT PMDB, PP, PTB PDT,PSB,PCdoB PM D B,PPS D EM,PFL PSDB PT PMDB,PP,PTBPTB Government Opposition 1999-2002 PR,PFL,PM D B PT PMDB, PP, PTB PDT,PSB,PCdoB PM D B,PPS D EM,PFL PSDB PT PMDB,PP,PTBPTB Government Opposition 2003-2006
- 138. Example: Brazilian chamber of deputies Voting network between members of congress (1999-2006) PMDB, PP, PT B DEM,PP PT PP,PMDB,PTB PDT ,PSB,PCdoBPTB,PMDBPSDB,PR DEM ,PFLPSDB PT PP,PTB Right Center Left PR,PFL,PM D B PT PMDB, PP, PTB PDT,PSB,PCdoB PM D B,PPS D EM,PFL PSDB PT PMDB,PP,PTBPTB Government Opposition 1999-2002 PR,PFL,PM D B PT PMDB, PP, PTB PDT,PSB,PCdoB PM D B,PPS D EM,PFL PSDB PT PMDB,PP,PTBPTB Government Opposition 2003-2006 log10 Λ ≈ −111 Λ = 1
- 139. Movement between groups... PT PMDB PD T,PSB PMDB P T PSB,PDT PP,PR, PTB PCdoB,PSB PSDB PFL,DEM PPS,PT
- 140. Networks with metadata Many network datasets contain metadata: Annotations that go beyond the mere adjacency between nodes. Often assumed as indicators of topological structure, and used to validate community detection methods. A.k.a. “ground-truth”.
- 141. Example: American college football Metadata (Conferences)
- 142. Example: American college football SBM fit
- 143. Example: American college football Discrepancy
- 144. Example: American college football Discrepancy Why the discrepancy? Some hypotheses:
- 145. Example: American college football Discrepancy Why the discrepancy? Some hypotheses: The model is not sufficiently descriptive.
- 146. Example: American college football Discrepancy Why the discrepancy? Some hypotheses: The model is not sufficiently descriptive. The metadata is not sufficiently descriptive or is inaccurate.
- 147. Example: American college football Discrepancy Why the discrepancy? Some hypotheses: The model is not sufficiently descriptive. The metadata is not sufficiently descriptive or is inaccurate. Both.
- 148. Example: American college football Discrepancy Why the discrepancy? Some hypotheses: The model is not sufficiently descriptive. The metadata is not sufficiently descriptive or is inaccurate. Both. Neither.
- 149. Model variations: Annotated networks M.E.J. Newman and A. Clauset, arXiv:1507.04001 Main idea: Treat metadata as data, not “ground truth”. Annotations are partitions, {xi} Can be used as priors: P(G, {xi}|θ, γ) = {bi} P(G|{bi}, θ)P({bi}|{xi}, γ) P({bi}|{xi}, γ) = i γbixu Drawbacks: Parametric (i.e. can overfit). Annotations are not always partitions.
- 150. Metadata is often very heterogeneous Example: IMDB Film-Actor network Data: 96, 982 Films, 275, 805 Actors, 1, 812, 657 Film-Actor Edges Film metadata: Title, year, genre, production company, country, user-contributed keywords, etc. Actor metadata: Name, Age, Gender, Nationality, etc. User-contributed keywords (93, 448) 100 101 102 103 104 k 100 101 102 103 104 105 Nk Keyword occurrence Number of keywords per film
- 151. Metadata is often very heterogeneous Example: IMDB Film-Actor network Keyword Occurrences ’independent-film’ 15513 ’based-on-novel’ 12303 ’character-name-in-title’ 11801 ’murder’ 11184 ’sex’ 9759 ’female-nudity’ 9239 ’nudity’ 5846 ’death’ 5791 ’husband-wife-relationship’ 5568 ’love’ 5560 ’violence’ 5480 ’police’ 5463 ’father-son-relationship’ 5063
- 152. Metadata is often very heterogeneous Example: IMDB Film-Actor network Keyword Occurrences ’independent-film’ 15513 ’based-on-novel’ 12303 ’character-name-in-title’ 11801 ’murder’ 11184 ’sex’ 9759 ’female-nudity’ 9239 ’nudity’ 5846 ’death’ 5791 ’husband-wife-relationship’ 5568 ’love’ 5560 ’violence’ 5480 ’police’ 5463 ’father-son-relationship’ 5063 Keyword Occurrences ’discriminaton-against-anteaters’ 1 ’partisan-violence’ 1 ’deliberately-leaving-something-behind’ 1 ’princess-from-outer-space’ 1 ’reference-to-aleksei-vorobyov’ 1 ’dead-body-on-the-beach’ 1 ’liver-failure’ 1 ’hit-with-a-skateboard’ 1 ’helping-blind-man-cross-street’ 1 ’abandoned-pet’ 1 ’retired-clown’ 1 ’resentment-toward-stepson’ 1 ’mutilating-a-plant’ 1
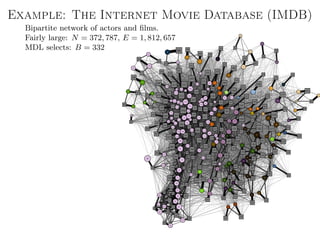
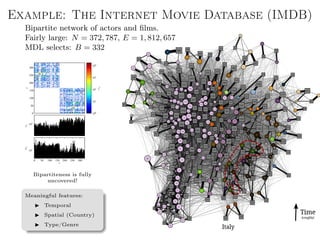
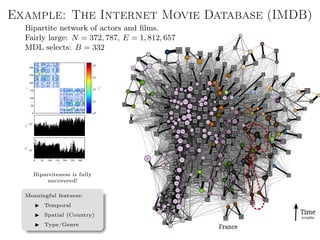
- 153. Better approach: Metadata as data Main idea: Treat metadata as data, not “ground truth”. Generalized annotations Aij → Data layer Tij → Annotation layer D ata, A M etad ata, T Joint model for data and metadata (the layered SBM [1]). Arbitrary types of annotation. Both data and metadata are clustered into groups. Fully nonparametric.
- 154. Example: American college football
- 155. Metadata and prediction of missing nodes Node probability, with known group membership: P(ai|A, bi, b) = θ P(A, ai|bi, b, θ)P(θ) θ P(A|b, θ)P(θ) Node probability, with unknown group membership: P(ai|A, b) = bi P(ai|A, bi, b)P(bi|b), Node probability, with unknown group membership, but known metadata: P(ai|A, T , b, c) = bi P(ai|A, bi, b)P(bi|T , b, c), Group membership probability, given metadata: P(bi|T , b, c) = P(bi, b|T , c) P(b|T , c) = γ P(T |bi, b, c, γ)P(bi, b)P(γ) bi γ P(T |bi, b, c, γ)P(bi, b)P(γ) Predictive likelihood ratio: λi = P(ai|A, T , b, c) P(ai|A, T , b, c) + P(ai|A, b) λi > 1/2 → the metadata improves the prediction task
- 156. Metadata and prediction of missing nodes
- 157. Metadata and prediction of missing nodes FB Penn PPI(krogan) FB Tennessee FB Berkeley FB Caltech FB Princeton PPI(isobasehs) PPI(yu) FB StanfordPGP PPI(gastric) FB Harvard FB Vassar Pol.Blogs PPI(pancreas)Flickr PPI(lung) PPI(predicted) AnobiiSNIM DBAmazon Debianpkgs.DBLP InternetAS APS citations LFR bench. 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 Avg.likelihoodratio,λ λi = P(ai|A, T , b, c) P(ai|A, T , b, c) + P(ai|A, b)
- 158. Metadata and prediction of missing nodes Metadata Data Aligned Misaligned Random 2 3 4 5 6 7 8 9 10 Number of planted groups, B 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 Averagepredictivelikelihoodratio,λ Aligned Random Misaligned Misaligned (N/B = 103)
- 159. Metadata predictiveness Neighbor probability: Pe(i|j) = ki ebi,bj ebi ebj Neighbour probability, given metadata tag: Pt(i) = j P(i|j)Pm(j|t) Null neighbor probability (no metadata tag): Q(i) = j P(i|j)Π(j) Kullback-Leibler divergence: DKL(Pt||Q) = i Pt(i) ln Pt(i) Q(i) Relative divergence: µr ≡ DKL(Pt||Q) H(Q) → Metadata group predictiveness Neighbour prob. without metadata i Q(i) Neighbour prob. with metadata iP(i)
- 160. Metadata predictiveness IMDB film-actor network 100 101 102 103 104 Metadata group size, nr 0.0 0.2 0.4 0.6 0.8 1.0 1.2 Metadatagrouppredictiveness,µr Keywords Producers Directors Ratings Country Genre Production Year
- 161. Metadata predictiveness APS citation network 100 101 102 Metadata group size, nr 0.0 0.2 0.4 0.6 0.8 1.0 Metadatagrouppredictiveness,µr Journal PACS Date
- 162. Metadata predictiveness Amazon co-purchases 101 102 103 104 Metadata group size, nr 0.0 0.2 0.4 0.6 0.8 1.0 Metadatagrouppredictiveness,µr Categories
- 163. Metadata predictiveness Internet AS 100 101 Metadata group size, nr 0.0 0.2 0.4 0.6 0.8 1.0 Metadatagrouppredictiveness,µr Country
- 164. Metadata predictiveness Facebook Penn State 100 101 102 103 Metadata group size, nr 0.0 0.2 0.4 0.6 0.8 1.0 Metadatagrouppredictiveness,µr Dorm Gender High School Major Year
- 165. n-order Markov chains with communities T. P. P. and Martin Rosvall, arXiv: 1509.04740 Transitions conditioned on the last n tokens p(xt|xt−1) → Probability of transition from memory xt−1 = {xt−n, . . . , xt−1} to token xt Instead of such a direct parametrization, we divide the tokens and memories into groups: p(x|x) = θxλbxbx θx → Overall frequency of token x λrs → Transition probability from memory group s to token group r bx, bx → Group memberships of tokens and groups t f s I e a w o h b m i h i t s w b o a f e m (a) I t w a s h e b o f i m (b) t he It of st as s f es t w be wa me e o b th im ti h i t w o a s b f e m (c) {xt} = "It␣was␣the␣best␣of␣times"
- 166. n-order Markov chains with communities {xt} = "It␣was␣the␣best␣of␣times" P({xt}|b) = dλdθ P({xt}|b, λ, θ)P(θ)P(λ) The Markov chain likelihood is (almost) identical to the SBM likelihood that gen- erates the bipartite transition graph. Nonparametric → We can select the number of groups and the Markov order based on statistical evidence! T. P. P. and Martin Rosvall, Nature Communications (in press)
- 167. Bayesian formulation P({xt}|b) = dθ dλ P({xt}|b, λ, θ) r Dr({θx}) s Ds({λrs}) Noninformative priors → Microcanonical model P({xt}|b) = P({xt}|b, {ers}, {kx}) × P({kx}|{ers}, b) × P({ers}), where P({xt}|b, {ers}, {kx}) → Sequence likelihood, P({kx}|{ers}, b) → Token frequency likelihood, P({ers}) → Transition count likelihood, − ln P({xt}, b) → Description length of the sequence Inference ↔ Compression
- 168. n-order Markov chains with communities US Air Flights War and peace Taxi movements “Rock you” password list n BN BM Σ Σ BN BM Σ Σ BN BM Σ Σ BN BM Σ Σ 1 384 365 364, 385, 780 365, 211, 460 65 71 11, 422, 564 11, 438, 753 387 385 2, 635, 789 2, 975, 299 140 147 1, 060, 272, 230 1, 060, 385, 582 2 386 7605 319, 851, 871 326, 511, 545 62 435 9, 175, 833 9, 370, 379 397 1127 2, 554, 662 3, 258, 586 109 1597 984, 697, 401 987, 185, 890 3 183 2455 318, 380, 106 339, 898, 057 70 1366 7, 609, 366 8, 493, 211 393 1036 2, 590, 811 3, 258, 586 114 4703 910, 330, 062 930, 926, 370 4 292 1558 318, 842, 968 337, 988, 629 72 1150 7, 574, 332 9, 282, 611 397 1071 2, 628, 813 3, 258, 586 114 5856 889, 006, 060 940, 991, 463 5 297 1573 335, 874, 766 338, 442, 011 71 882 10, 181, 047 10, 992, 795 395 1095 2, 664, 990 3, 258, 586 99 6430 1, 000, 410, 410 1, 005, 057, 233 gzip 573, 452, 240 9, 594, 000 4, 289, 888 1, 315, 388, 208 LZMA 402, 125, 144 7, 420, 464 2, 902, 904 1, 097, 012, 288 (SBM can compress your files!) T. P. P. and Martin Rosvall, arXiv: 1509.04740
- 169. n-order Markov chains with communities Example: Flight itineraries xt = {xt−3, Altanta|Las Vegas, xt−1} { { T. P. P. and Martin Rosvall, arXiv: 1509.04740
- 170. Dynamic networks Each token is an edge: xt → (i, j)t Dynamic network → Sequence of edges: {xt} = {(i, j)t} Problem: Too many possible tokens! O(N2 ) Solution: Group the nodes into B groups. Pair of node groups (r, s) → edge group. Number of tokens: O(B2 ) O(N2 ) Two-step generative process: {xt} = {(r, s)t} (n-order Markov chain of pairs of group labels) P((i, j)t|(r, s)t) (static SBM generating edges from group labels) T. P. P. and Martin Rosvall, arXiv: 1509.04740
- 171. Dynamic networks Example: Student proximity Static part PC PCstMPst1 M P MPst2 2BIO 1 2BIO22BIO3 PSIst T. P. P. and Martin Rosvall, arXiv: 1509.04740
- 172. Dynamic networks Example: Student proximity Static part PC PCstMPst1 M P MPst2 2BIO 1 2BIO22BIO3 PSIst Temporal part T. P. P. and Martin Rosvall, arXiv: 1509.04740
- 173. Dynamic networks in continuous time xτ → token at continuous time τ P({xτ }) = P({xt}) Discrete chain × P({∆t}|{xt}) Waiting times Exponential waiting time distribution P({∆t}|{xt}, λ) = x λ kx bx e−λbx ∆x Bayesian integrated likelihood P({∆t}|{xt}) = r ∞ 0 dλ λer e−λ∆r P(λ|α, β), = r Γ(er + α)βα Γ(α)(∆r + β)er+α . Hyperparameters: α, β. Noninformative limit α → 0, β → 0 leads to Jeffreys prior: P(λ) ∝ 1 λ T. P. P. and Martin Rosvall, arXiv: 1509.04740
- 174. Dynamic networks Continuous time {xτ } → Sequence of notes in Beethoven’s fifth symphony 0 4 8 12 16 20 Memory group 10−4 10−3 10−2 10−1 Avg.waitingtime(seconds) Without waiting times (n = 1) 0 4 8 12 16 20 24 28 32 Memory group 10−7 10−6 10−5 10−4 10−3 10−2 10−1 Avg.waitingtime(seconds) With waiting times (n = 2)
- 175. Nonstationarity Dynamic networks {xt} → Concatenation of “War and peace,” by Leo Tolstoy, and “ `A la recherche du temps perdu,” by Marcel Proust. Unmodified chain Tokens Memories − log2 P({xt}, b) = 7, 450, 322
- 176. Nonstationarity Dynamic networks {xt} → Concatenation of “War and peace,” by Leo Tolstoy, and “ `A la recherche du temps perdu,” by Marcel Proust. Unmodified chain Tokens Memories − log2 P({xt}, b) = 7, 450, 322 Annotated chain xt = (xt, novel) Tokens Memories − log2 P({xt}, b) = 7, 146, 465
- 177. Latent space models P. D. Hoff, A. E. Raferty, and M. S. Handcock, J. Amer. Stat. Assoc. 97, 1090–1098 (2002) P(G|{xi}) = i>j p Aij ij (1 − pij)1−Aij pij = exp − (xi − xj)2 . (Human connectome) Many other more elaborate embeddings (e.g. hyperbolic spaces). Properties: Softer approach: Nodes are not placed into discrete categories. Exclusively assortative structures. Formulation for directed graphs less trivial.
- 178. Discrete vs. continuous Can we formulate a unified parametrization?
- 179. The Graphon P(G|{xi}) = i>j p Aij ij (1 − pij)1−Aij pij = ω(xi, xj) xi ∈ [0, 1] Properties: Mostly a theoretical tool. Cannot be directly inferred (without massively overfitting). Needs to be parametrized to be practical.
- 180. The SBM → a piecewise-constant Graphon ω(x, y)
- 181. A “soft” graphon parametrization M.E.J. Newman, T. P. Peixoto, Phys. Rev. Lett. 115, 088701 (2015) puv = dudv 2m ω(xu, xv) ω(x, y) = N j,k=0 cjkBj(x)Bk(y) Bernstein polynomials: Bk(x) = N k xk (1−x)N−k , k = 0 . . . N 0.0 0.2 0.4 0.6 0.8 1.0 x 0.0 0.2 0.4 0.6 0.8 1.0 Bk(x) k = 0 k = 1 k = 2 k = 3 k = 4 k = 5
- 182. A “soft” graphon parametrization M.E.J. Newman, T. P. Peixoto, Phys. Rev. Lett. 115, 088701 (2015) puv = dudv 2m ω(xu, xv) ω(x, y) = N j,k=0 cjkBj(x)Bk(y) Bernstein polynomials: Bk(x) = N k xk (1−x)N−k , k = 0 . . . N 0.0 0.2 0.4 0.6 0.8 1.0 x 0.0 0.2 0.4 0.6 0.8 1.0 Bk(x) k = 0 k = 1 k = 2 k = 3 k = 4 k = 5 ω(x, y)
- 183. Inferring the model Semi-parametric Bayesian approach Expectation-Maximization algorithm 1. Expectation step q(x) = P(A, x|c) P(A, x|c)dnx 2. Maximization step P(A|c) = P(A, x|c)dn x ˆcjk = argmax cjk P(A|c) Belief-Propagation ηu→v(x) = 1 Zu→v exp − w dudw 1 0 qw(y)ω(x, y)dy × w(=v) auw=1 1 0 ηw→u(y)ω(x, y)dy, quv(x, y) = ηu→v(x)ηv→u(y)ω(x, y) 1 0 ηu→v(x)ηv→u(y)ω(x, y)dxdy . Algorithmic complexity: O(mN2)
- 184. Example: SBM sample
- 185. Example: School friendships 12 14 16 18 Age 0 1Nodeparameter
- 186. Example: C. elegans worm
- 187. Example: C. elegans worm