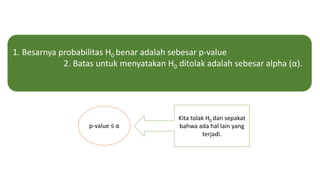
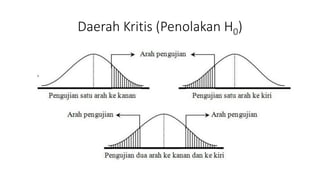
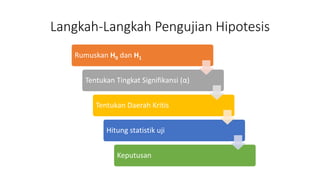
Dokumen tersebut membahas tentang pengujian hipotesis statistik untuk mengetahui apakah mean time response situs e-commerce memenuhi kriteria tertentu. Hipotesis nol menyatakan bahwa mean time response adalah sama dengan 2,5 detik, sedangkan hipotesis alternatif menyatakan kurang dari 2,5 detik. Dokumen tersebut juga menjelaskan langkah-langkah pengujian hipotesis statistik seperti menentukan tingkat signifikansi, daerah

1. Probability & Statistics
Statistical Hypothesis
Dibuat oleh: Bayu Rima Aditya

2. Layanan pesaing aku sudah ditutup..
Ini kesempatanku.. Tapi…apakah
mean time response situs e-
commerceku mampu menyaingi
performansi situs dia yang mencapai
2,5 detik?
Aku harus survey ke user untuk
menguji apakah mean time response
user terhadap situs e-commerce aku
adalah kurang dari 2,5 detik.

3. Contoh Hasil Survey
Dari 100 user yang sering
menggunakan situs e-
commerce Donal Duck,
diperoleh mean time
response yang mereka alami
untuk satu klik permintaan
layanan adalah 2,25 detik.

4. Hipotesis Nol : Mean time response e-commerce Donald Duck sama dengan 2,5 detik ; μ = 2,5 detik
Hipotesis Alternatif : Mean time response e-commerce Donald Duck kurang dari 2,5 detik ; μ < 2,5 detik
Dimulai dengan asumsi
bahwa hipotesis nol
adalah benar

5. Penentuan apakah
H0 diterima (dianggap
benar) atau ditolak
(dianggap salah)
adalah merupakan tujuan
dari pengujian Hipotesis
Statistik.

6. Hipotesis Statistik
1. Hipotesis Statistik adalah suatu proporsi atau anggapan mengenai
paramaeter populasi yang dapat diuji secara statistik melalui
sampel yang diambel populasi.
2. Hipotesis statistik terdiri dari hipotesis nol (H0) dan hipotesis
alternatif (H1).
3. H0 dan H1 adalah mutually exclusive dan exhaustive (lengkap)

7. H0 : Tidak ada perbedaan (sama / “=“) rata-rata lama
waktu pengerjaan staff IT untuk membuat suatu aplikasi
android.
H1 : Ada perbedaan rata-rata lama waktu pengerjaan
staff IT untuk membuat suatu aplikasi android.
Contoh Hipotesis Statistik
H0 : Tidak ada hubungan antara lokasi download dengan
kecepatan download.
H1 : Ada hubungan antara lokasi download dengan
kecepatan download.

8. Penulisan Hipotesis untuk Mean
Bentuk penulisan hipotesis satu arah untuk mean:
H0 : µ = µ0 atau H0 : µ = µ0
H1 : µ < µ0 H1 : µ > µ0
Bentuk penulisan hipotesis dua arah untuk mean:
H0 : µ = µ0
H1 : µ ≠ µ0

9. Penulisan Hipotesis untuk Proporsi
Bentuk penulisan hipotesis satu arah untuk proporsi:
H0 : p = p0 atau H0 : p = p0
H1 : p < p0 H1 : p > p0
Bentuk penulisan hipotesis dua arah untuk proporsi:
H0 : p = p0
H1 : p ≠ p0

10. Bagaimana dengan
alpha (α)?
Bagaimana dengan p-
value?
Bagaimana dengan
daerah penolakan?
Bagaimana dengan
statistik uji?

11. 1. Besarnya probabilitas H0 benar adalah sebesar p-value
2. Batas untuk menyatakan H0 ditolak adalah sebesar alpha (α).
Kita tolak H0 dan sepakat
bahwa ada hal lain yang
terjadi.
p-value ≤ α

12. Untuk kegiatan ilmiah,
sering digunakan
tingkat α sebesar 0,05
atau 0,01

13. Statistik Uji
Suatu metode statistik yang digunakan
untuk menganalisis bukti terhadap
hipotesis nol.
Sampel Besar n ≥ 30 Sampel Kecil n < 30
Uji z Uji t

14. Daerah Kritis (Penolakan H0)

15. Langkah-Langkah Pengujian Hipotesis
Rumuskan H0 dan H1
Tentukan Tingkat Signifikansi (α)
Tentukan Daerah Kritis
Hitung statistik uji
Keputusan

16. Pengujian μ = μ0; Sampel Besar
1. H0 : μ = μ 0
2. H1 : alternatif
a. μ < μ0
b. μ > μ0
c. μ ≠ μ0
3. Tentukan level of sgnifikansi atau α.
4. Daerah Kritis
a. untuk H1 : μ < μ0
b. untuk H1 : μ > μ0
c. untuk H1 : µ ≠ µ0
5. Hitung 𝑥 dan s dari sampel acak berukuran n. Kemudian hitung nilai statistik uji
6. Keputusan: Tolak H0 jika nilai statistik uji (z) jatuh pada daerah kritis.
zz 
zz 
22
 zzorzz 
n
s
x
XSE
x
z 00
)(
 




17. Pengujian μ = μ0; Sampel Kecil
1. H0 : μ = μ 0
2. H1 : alternatif
a. μ < μ0
b. μ > μ0
c. μ ≠ μ0
3. Tentukan level of sgnifikansi atau α.
4. Daerah Kritis
a. untuk H1 : μ < μ0
b. untuk H1 : μ > μ0
c. untuk H1 : µ ≠ µ0
5. Hitung 𝑥 dan s dari sampel acak berukuran n. Kemudian hitung nilai statistik uji
6. Keputusan: Tolak H0 jika nilai statistik uji (t) jatuh pada daerah kritis.
tt 
tt 
22
 ttortt 
n
s
x
XSE
x
t 00
)(
 


