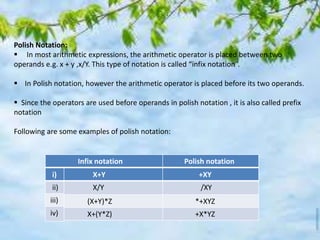
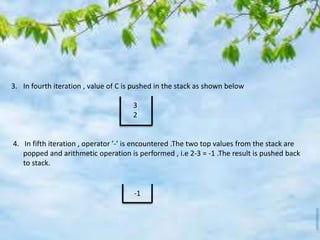
The document discusses stacks and their implementation in computer programs. It defines a stack as a linear data structure that only allows two operations - insertion and deletion from one end. Common examples provided are a dish rack and array-based implementation in memory. Key points covered include LIFO behavior, push and pop operations, algorithms to implement these, and using a stack to evaluate postfix expressions by operating on elements in the order they are encountered. An example calculation is presented to demonstrate the postfix evaluation process step-by-step using a stack.

3. Presentation topic:
Stack
Group members:
Iqra Zubair
BSCS(3rd)
Roll#12
Hira Bashir
BSCS(3rd)
Roll#15

4. What is stack?
Stack:
“ A stack is a special kind of linear list in which only two operations, insertion and
deletion can be performed.”
The items in it are stored and retrieved in LIFO manner.
L Last
I In
F First
O Out

5. A common example of stack is a dish rack. A dish rack is a spring loaded
device that holds dishes such in a manner that only the top dish is visible. It is used
such that
 A clean dish is placed on the top of the stack. This forces the spring down and
only the new dish is available.
 When a clean dish is needed, the top one is removed. This causes the spring to
release so that the second dish becomes available.
 The last dish cleaned is a first one used.
Example:

6. A stack is usually represented by a linear array in the computer memory
93 51 77 38
1 2 3 4 5 6 7 8 9 10
Bottom top
The most accesible item in the stack is called Top of the stack and the least accessible
item is called Bottom of the stack.
Stack Operations:
The only two operations that can be performed on a stack are:
 insertion (Pushing)
 deletion (Popping)

7. Insertion:
The process of insertion or adding new items into stack is called Pushing.
• Before pushing an item into a stack, it is tested whether or not there is any vacancy in
the stack to store the item.
• If there is no vacancy in the stack then the stack condition is known as overflow.
Deletion:
This process of removing or deleting items from a stack is called Popping.
• Before pushing an item from a stack, it is tested whether or not there at least one
element present in the stack to delete the item.
• If there is no element exist in the stack i.e,the stack is empty, then the stack condition
is known as underflow.

8. Algorithm: (Push procedure-Push(S,X)) :
Suppose the stack has N elements and pointer Top represents the top element in the
stack. The algorithm is as follow:
1. [Check for overflow condition]
IF Top > = N then
PRINT “Stack is overflow”.
RETURN
[End of IF Structure]
2. [Increment 1 Into Top]
Top=Top+1
3. [Add element X into Stack “S”]
S[Top] = X
[End of procedure]
4. RETURN

9. The algorithm is as follow:
1. [Check for Underflow condition]
IF Top > = 0 then
PRINT “Stack is underflow”.
RETURN
[End of IF Structure]
2. [Decrement 1 from Top]
Top=Top-1
[End of procedure]
4. RETURN
Algorithm: (Pop procedure-Push(S , Top)) :

10. // program to push and pop items in a stack .
#include<iostream.h>
#include<conio.h>
class stack
{
private:
int top;
int S[10];
public:
// constructor to initialize a stack
stack();
{
top = -1;
}
// member function to push item into stack
push (int n)
{
If(top == 9)
Code:

11. {
cout<<“Stack overflow”;
getch();
return 0;
}
top ++;
S[top] = n;
}
// member function to delete item from stack
int pop()
{
if (top==-1)
{
cout<<“Stack is empty;”
getch();
return NULL;
}
data=S[top] ;
top - -;
return data;
}

12. // member function to print item of stack
print()
{
if(top==-1)
{
cout<<“Stack is empty”;
return NULL;
; }
for(int i=top; i>0 ; i - -)
cout<<S[i]<<endl;
getch();
}
};
main()
{
stack obj ;
int opt , val ;
while(opt!=3)

13. clrscr();
cout<<“1: Pushn”;
cout<<“2: Popn”;
cout<<“3: Exitn”;
cout<<“ Enter the choicen”;
cin>>opt
cout<<“1: Pushn”;
cout<<“2: Popn”;
cout<<“3: Exitn”;
cout<<“ Enter the choicen”;
cin>>opt;
switch(opt)
{
case 1:
cout<<“Enter Value to insert?”;
cin>>val ;

14. obj.print();
break();
case 2:
cout<< “n Value “<<obj.pop()<<“is poppedn”;
obj.print();
break;
}
}
}

15. Infix notation Polish notation
i)
ii)
iii)
iv)
X+Y +XY
X/Y /XY
(X+Y)*Z *+XYZ
X+(Y*Z) +X*YZ
Polish Notation:
 In most arithmetic expressions, the arithmetic operator is placed between two
operands e.g. x + y ,x/Y. This type of notation is called “infix notation”.
 In Polish notation, however the arithmetic operator is placed before its two operands.
 Since the operators are used before operands in polish notation , it is also called prefix
notation
Following are some examples of polish notation:

16. The polish notation is named in honour of Polish mathematicians Jan Lukasiewiez.
Note: Parenthesis are not used in polish notation.
The computer evaluates an expression given in infix notation by converting
it into postfix notation .
The stack is used to perform this operation.

17. The following steps are taken to evaluate a postfix expression:
 The expression is scanned from left to right until the end of the expression.
 When an operator is encountered, it is pushed into stack.
 When an operator is encountered, then:
 The top two operands of stack are removed.
The arithmetic operation is performed.
The computed result is pushed back to the stack.
 When end of the expression is reached, the top value from the stack is picked. It is the
computed value of the expression.

18. Example:
Evaluate expression AB/C-DE*+ when A=12, B=6, C=3, D=4, E=5.
1. In first and second iteration, the values of A and B are pushed into the stack as
shown below:
2. In the third iteration, the operator ‘ / ’ is encountered. So, the two values 6 and 12
are removed from stack and division is performed, i.e. 12 / 6 = 2. The computed
value is pushed back to the stack. The values in the stack will be:
6
12
2

19. 3. In fourth iteration , value of C is pushed in the stack as shown below
4. In fifth iteration , operator ’-’ is encountered .The two top values from the stack are
popped and arithmetic operation is performed , i.e 2-3 = -1 .The result is pushed back
to stack.
3
2
-1

20. 5 . In sixth and seventh iterations , value of D and E are pushed into the stack as
shown below:
6 . In eight iteration , multiplication operator * is encountered , Thus 4 & 5 are
popped .
Multiplication operation is performed and calculated result 20 is pushed in the
stack .
The stack will be shown below
5
4
-1
20
-1

21. 7 . In ninth repetition the operator ‘+’ is encountered . Two values 20 and -1 are
popped .
The addition of these numbers is performed and the result 19 is pushed
back to stack.
8 . The top value in stack is 19 . It is the final value after evaluating the
expression:
12 / 6 – 3 + 4 * 5 =
= 2 – 3 + 20
= -1 + 20
= 19
19