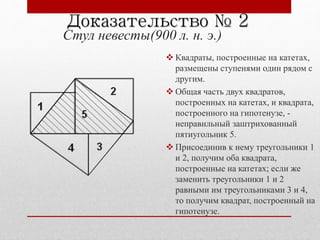
Документ обсуждает теорему Пифагора, её исторические корни, начиная с Древнего Китая и Египта. Приводятся алгебраическая и геометрическая формулировки теоремы, а также несколько различных доказательств. Отмечается, что теорема сохраняет свою актуальность и точность на протяжении веков.

1. Теорема
Пифагора
Подготовил:
Федотов Александр,
ученик 9А класса
гимназии №18

2. Из истории теоремы
Своё начало теорема берёт из Древнего Китая. В
математической книге Чу-пей так говорится о
Пифагоровом треугольнике со сторонами 3, 4 и 5:
"Если прямой угол разложить на составные
части, то линия, соединяющая концы его сторон,
будет 5, когда основание есть 3, а высота 4".

3. Теорема Пифагора в Египте
• Кантор (крупнейший
немецкий историк
математики) считает, что
равенство 3² + 4² = 5²
• было известно
египтянам еще в 2300 году
до н. э.
Кантор

4. Теорема в Вавилоне
• В одном тексте,
относимом ко
времени
Хаммураби, т. е. к
2000 г. до н. э.,
приводится
приближенное
вычисление
гипотенузы
прямоугольного
треугольника.

5. "Заслугой первых греческих
математиков, таких как
Фалес, Пифагор и
пифагорейцы, является не
открытие математики, но
ее систематизация и
обоснование. В их руках
вычислительные рецепты,
основанные на смутных
представлениях,
превратились в точную
науку."
Ван-Дер-Варден

6. Краткая биография Пифагора
Пифагор Самосский -
древнегреческий математик и
философ-идеалист. Получил
хорошее образование. По
преданию Пифагор, чтобы
ознакомиться с мудростью
восточных ученых, выехал в
Египет и прожил там 22 года.

7. • Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвопринашенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
• Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее учуя ,вслед.
Они не в силах свету помешать ,
А могут лишь закрыв глаза дрожать
От страха, что вселил в них Пифагор.

8. Алгебраическая формулировка :
“ В прямоугольном треугольнике
квадрат длины гипотенузы равен
сумме квадратов длин катетов”.
𝒂 𝟐 + 𝒃 𝟐 = 𝒄 𝟐, где a и b – катеты,
а c –гипотенуза.
с
a
b
Теорема имеет алгебраическую и геометрическую трактовку.

9. Геометрическая формулировка :
“В прямоугольном треугольнике
площадь квадрата, построенного
на гипотенузе, равна сумме площадей
квадратов, построенных на катетах”.

10. для ΔABC: квадрат,
построенный на
гипотенузе АС, содержит 4
исходных треугольника, а
квадраты, построенные на
катетах, - по два. Теорема
доказана.
Доказательство № 1

11. Стул невесты(900 л. н. э.)
 Квадраты, построенные на катетах,
размещены ступенями один рядом с
другим.
 Общая часть двух квадратов,
построенных на катетах, и квадрата,
построенного на гипотенузе, -
неправильный заштрихованный
пятиугольник 5.
 Присоединив к нему треугольники 1
и 2, получим оба квадрата,
построенные на катетах; если же
заменить треугольники 1 и 2
равными им треугольниками 3 и 4,
то получим квадрат, построенный на
гипотенузе.
Доказательство № 2

12. a
Интересно это доказательство тем,
что рисунок сопровождался лишь
криком: “Смотри!”
Сторона маленького квадрата, получившегося в
центре, равна c - a , тогда:
222222
22)(24 caccaacaaccab 
Доказательство № 3

13. Доказательство № 4
(через подобные треугольники)
• Пусть ABC - прямоугольный треугольник с прямым углом C.
Проведём высоту из C и обозначим её основание через H.
Треугольник ACH подобен треугольнику ABC по двум углам.
Аналогично, треугольник CBH подобен ABC. Введя обозначения:
• |BC|=a; |AC|=b; |AB|=c
• Получаем:
• Сложив, получаем
• Или 𝑎2 + 𝑏2 = 𝑐2
b
AH
c
b
a
HB
c
a ||
;
||

222
|)||(| cAHHBcba 
С
А
B
H

14. Достроим треугольник до квадрата
со стороной равной a + b. Площадь
S этого квадрата равна (a + b)². С
другой стороны, этот квадрат
составлен из четырёх равных
прямоугольных треугольников,
площадь каждого из которых
равна 0.5ab и квадрата со стороной
c. Поэтому:
Доказательство № 5
22
2
2
1
4 cabcabS 
c
b
a
a
a
a
c
c c
c
b
b
b

15. Итог :