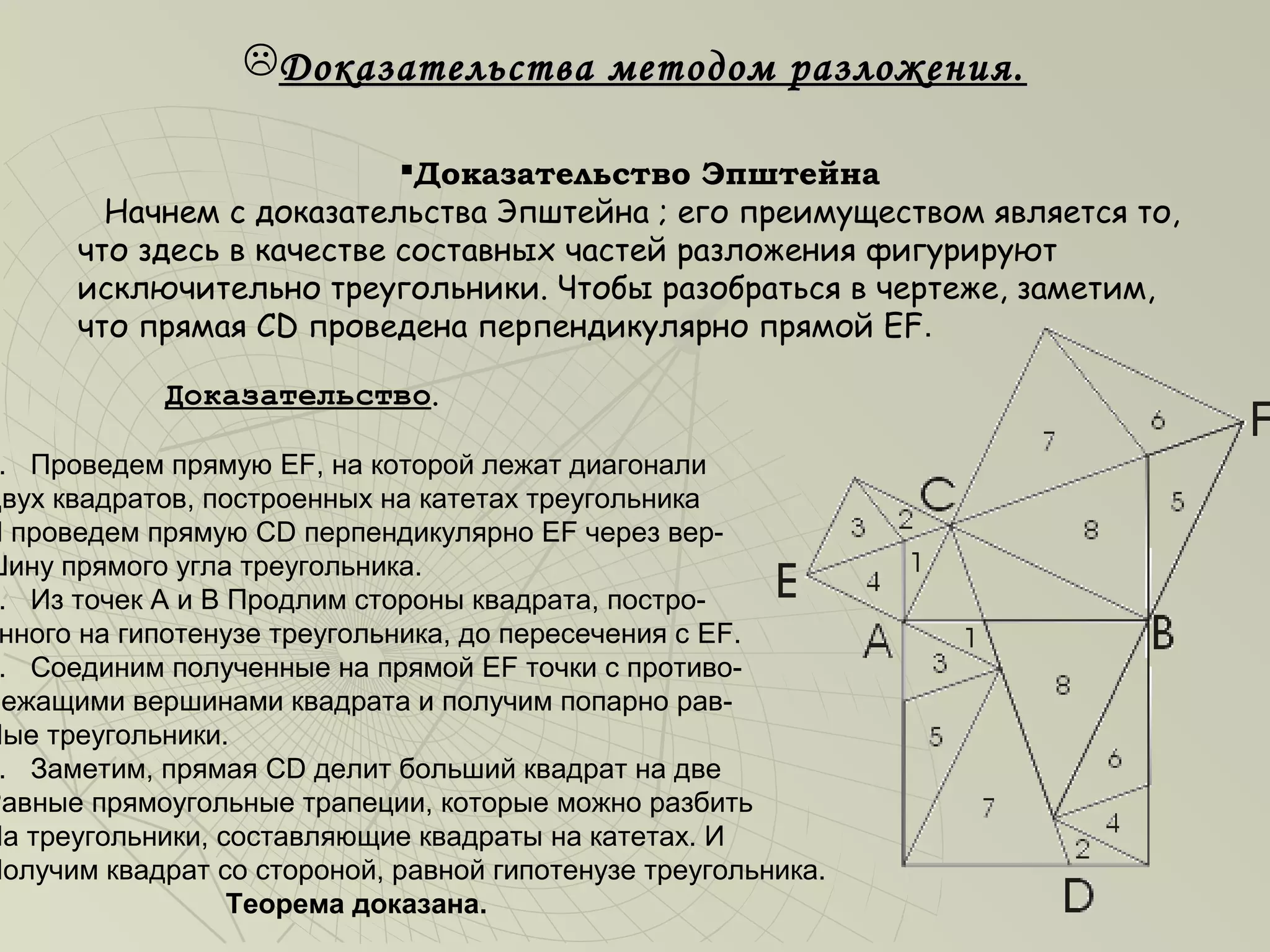
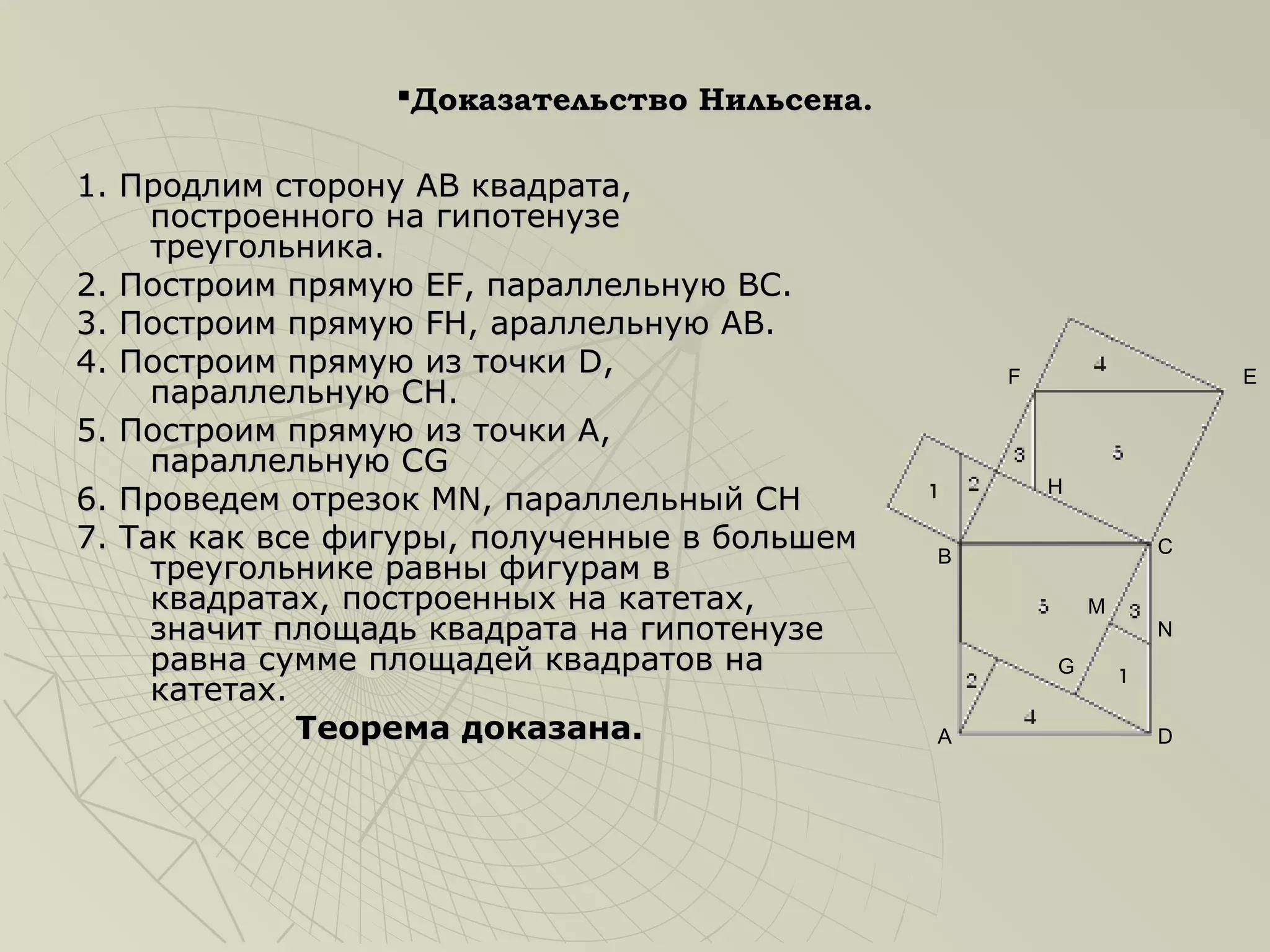
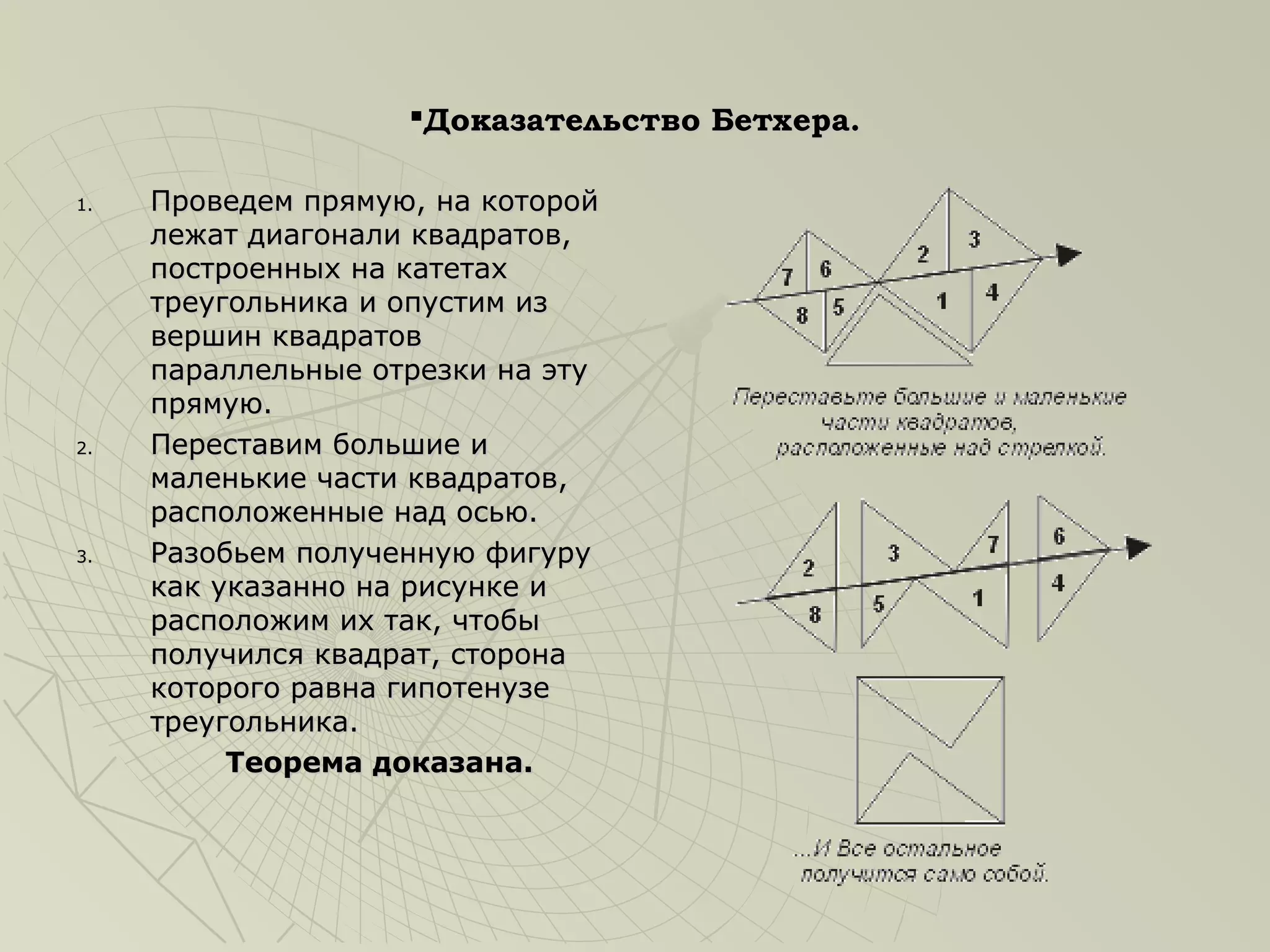
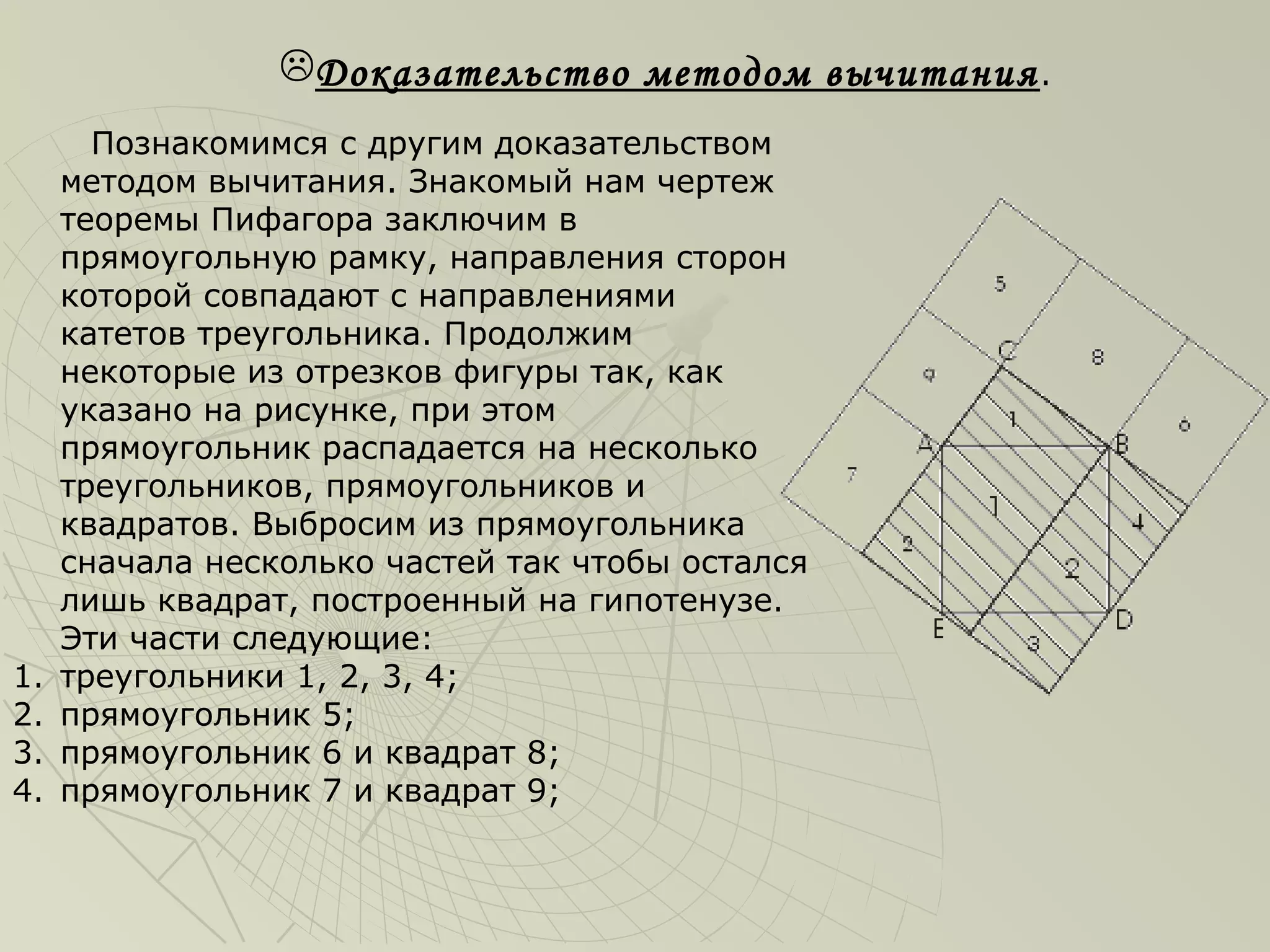
Документ охватывает историю и доказательства теоремы Пифагора, начиная с древнего Китая и Египта, где уже использовались примеры чисел 3, 4 и 5. Он содержит биографические данные о Пифагоре и различные методы доказательства теоремы, включая простейшие и более сложные подходы, такие как методы разложения и вычитания. Также упоминаются известные историки математики и их вклад в изучение теоремы, что подчеркивает её значимость в математике.