Презентация с доклада об идиоматичном ФП-коде и функциональных идиомах "зиппер", "комонада". #1 LambdaNsk

1. Идиоматичный
функциональный код
Александр Гранин
graninas@gmail.com

2. Изменяемое состояние
Присваивание
Сторонние эффекты
Методы, функции
Циклы
Базовые типы
Иммутабельность
Декларация
Чистые функции
Функции, лямбды
Рекурсия
Базовые типы
Императивное
программирование
Функциональное
программирование

3. Класс = поля + методы
Объект класса
Наследование, ассоциация
Функторы, делегаты
Интерфейсы
ООП-паттерны
Модуль = типы + функции
Значение АТД
Комбинаторы, композиция
Лямбды, ФВП, продолжения
Обобщение типов
???
Объектно -
ориентированное
программирование
Функциональное
программирование

4. Класс = поля + методы
Объект класса
Наследование, ассоциация
Функторы, делегаты
Интерфейсы
ООП-паттерны
Модуль = типы + функции
Значение АТД
Комбинаторы, композиция
Лямбды, ФВП, продолжения
Обобщение типов
Функциональные идиомы
Объектно -
ориентированное
программирование
Функциональное
программирование

5. Функциональные идиомы
● Foldable, Traversable
● Functors
● Applicative Functors
● Monoids
● Monads
● ...
● Existential types
● Lenses
● Zippers
● Comonads
● GATDs
● ...

6. Функциональные идиомы
● Foldable, Traversable
● Functors
● Applicative Functors
● Monoids
● Monads
● Existential types
● Lenses
● Zippers
● Comonads
● GATDs
В чем разница между понятиями
“ООП-паттерн” и “ФП-идиома”?

7. ООП-паттерн vs Идиома
Паттерн: подход “снаружи”.
Несколько классов связываются в единую
систему с обобщающими интерфейсами.
Идиома: подход “изнутри”.
Идиома структурирует данные, обобщает и
пополняет их свойства.

8. Zippers
http://design.vidanto.com/?p=225

9. Список
-- Список на АТД:
data List a = Empty | Cons a (List a)
myList1 = Cons 1 (Cons 2 (Cons 3 Empty))
-- Списки в Haskell:
myList1 = [1, 2, 3]
myList2 = 1 : 2 : 3 : []
myList3 = 1 : [2, 3]
http://learnyouahaskell.com/zippers

10. Zipper для списка
data Zipper a = Zip [a] a [a]
toLeft (Zip xs a (y:ys)) = Zip (a:xs) y ys
toRight (Zip (x:xs) a ys) = Zip xs x (a:ys)
extract (Zip _ a _) = a
http://learnyouahaskell.com/zippers

11. Zipper для списка
zipper = Zip [] 0 [1..10]
> toLeft zipper
Zip [0] 1 [2, 3, 4, 5, 6, 7, 8, 9, 10]
> extract (toLeft (toLeft zipper))
2

12. Zip [2, 1, 0] 3 [4..10]
Текущий элемент
Сохраненный Контекст

13. data Tree a = Empty | Node a (Tree a) (Tree a)
data Direction = L | R
modify :: (a -> a) -> Tree a -> [Direction] -> Tree a
Дерево
1
2
5 3
1
2
50 30

14. data Tree a = Empty | Node a (Tree a) (Tree a)
data Direction = L | R
modify :: (a -> a) -> Tree a -> [Direction] -> Tree a
newTree1 = modify (*10) myTree [R, L]
newTree2 = modify (*10) newTree1 [R, R]
Изменение дерева
1
2
50 30

15. data Tree a = Empty | Node a (Tree a) (Tree a)
data NodeCtx a = LCtx a (Tree a)
| RCtx a (Tree a)
data TreeZipper a = TZ (Tree a) [NodeCtx a]
extract (TZ (Node a _ _) _) = a
Zipper для дерева

16. goLeft :: TreeZipper a -> TreeZipper a
goLeft (TZ (Node a l r) ctxs) = (TZ l (LCtx a r : ctxs))
goRight :: TreeZipper a -> TreeZipper a
goRight (TZ (Node a l r) ctxs) = (TZ r (RCtx a l : ctxs))
goUp :: TreeZipper a -> TreeZipper a
goUp = ...
Zipper для дерева

17. 2
35 RCtx 1
> goRight zipper
TZ (Node 2 (Node 5 Empty Empty)
(Node 3 Empty Empty))
[RCtx 1 Empty]
1
2
35
tree = Node 1
Empty
(Node 2
(Node 5 Empty Empty)
(Node 3 Empty Empty))
zipper = TZ tree []

18. fromZipper :: TreeZipper a -> Tree a
fromZipper (TZ cur []) = cur
fromZipper z = fromZipper (goUp z)
Сборка дерева
RCtx 1
LCtx 2 3
5
1
2
35

19. data TreeDir = U | L | R
modify :: (a -> a) -> TreeZipper a -> [TreeDir] -> TreeZipper a
modify f (TZ (Node a l r) ctxs) [] = TZ (Node (f a) l r) ctxs
modify f z (L:dirs) = modify f (goLeft z) dirs
modify f z (R:dirs) = modify f (goRight z) dirs
modify f z (U:dirs) = modify f (goUp z) dirs
Изменение дерева

20. tree = Node 1
Empty
(Node 2
(Node 5 Empty Empty)
(Node 3 Empty Empty))
zipper = TZ tree []
newZipper1 = modify (*10) zipper [R, L]
newZipper2 = modify (*10) newZipper1 [U, R]
newTree = fromZipper newZipper
Изменение дерева 1
2
5 3
1
2
50 30

21. Комонады
https://greyfog.files.wordpress.com/2010/02/esploso-cellular-
automata.jpg

22. “Жизнь” без идиом
type Cell = (Int, Int)
type Grid = [Cell]
step :: Grid -> Grid
step p = let
next all [] = []
next all cur@((aX, aY) : alives) =
[(x, y) | x <- lim aX, y <- lim aY, length (neighbours8 (x, y) all) == 3]
++ (next all alives)
alive all cell = length (neighbours8 cell all) `elem` [2,3]
in L.nub $ filter (alive p) p ++ (next p p)

23. “Жизнь” без идиом
type Cell = (Int, Int)
type Grid = [Cell]
step :: Grid -> Grid
step p = let
next all [] = []
next all cur@((aX, aY) : alives) =
[(x, y) | x <- lim aX, y <- lim aY, length (neighbours8 (x, y) all) == 3]
++ (next all alives)
alive all cell = length (neighbours8 cell all) `elem` [2,3]
in L.nub $ filter (alive p) p ++ (next p p)
这是什么？

24. “Жизнь” на монадах
type Cell = (Int, Int)
type Grid = [Cell]
step :: Grid -> Grid
step cells = do
(newCell, n) <- frequencies $ concatMap neighbours cells
guard $ (n == 3) || (n == 2 && newCell `elem` cells)
return newCell
http://rhnh.net/2012/01/02/conway's-game-of-life-in-haskell

25. “Жизнь” на комонадах и зипперах
data Universe a = Universe [a] a [a]
data Cell = Dead | Alive
newtype Grid = Grid (Universe (Universe Cell))
rule :: Grid Cell -> Cell
rule grid
| nc == 2 = extract grid
| nc == 3 = Alive
| otherwise = Dead
where nc = length $ filter (==Alive) (neighbours grid)
next grid = grid =>> rule
http://habrahabr.ru/post/225473/

26. Множество Кантора на комонадах

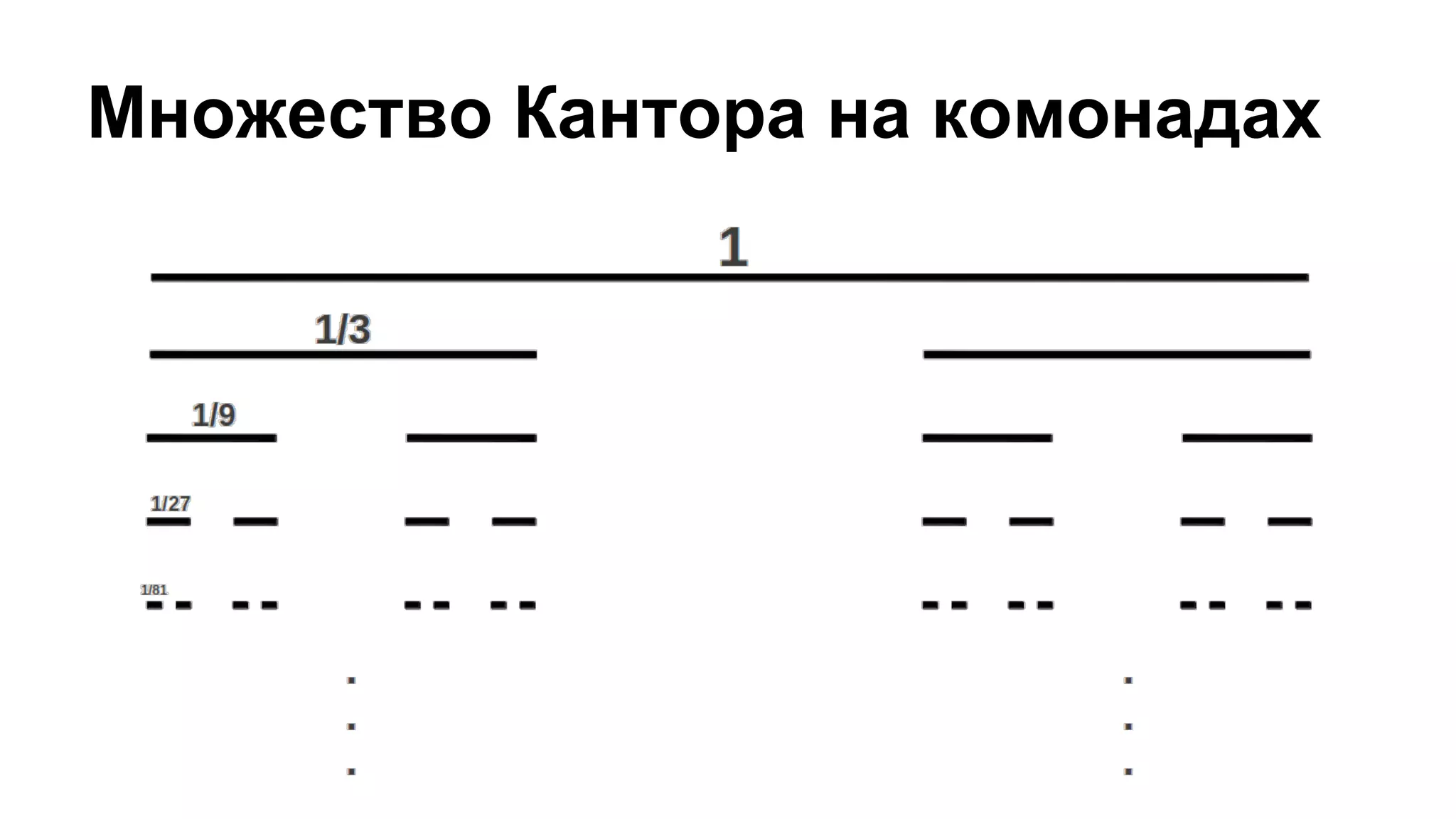
27. Правило вывода
type Segment = (Float, Float)
type Segments = [(Float, Float)]
cantorRule :: Segment -> Segments
cantorRule (x1, x2) = let
len = x2 - x1
oneThird = len / 3.0
in [(x1, x1 + oneThird), (x2 - oneThird, x2)]

28. Фрактал - список списков
cantorGen :: Segments -> Segments
cantorGen segs = concatMap cantorRule segs
fractal :: [Segments]
fractal = iterate cantorGen [(0.0, 0.9)]
> take 2 fractal
[ [(0.0,0.9)], [(0.0,0.3),(0.6,0.9)] ]

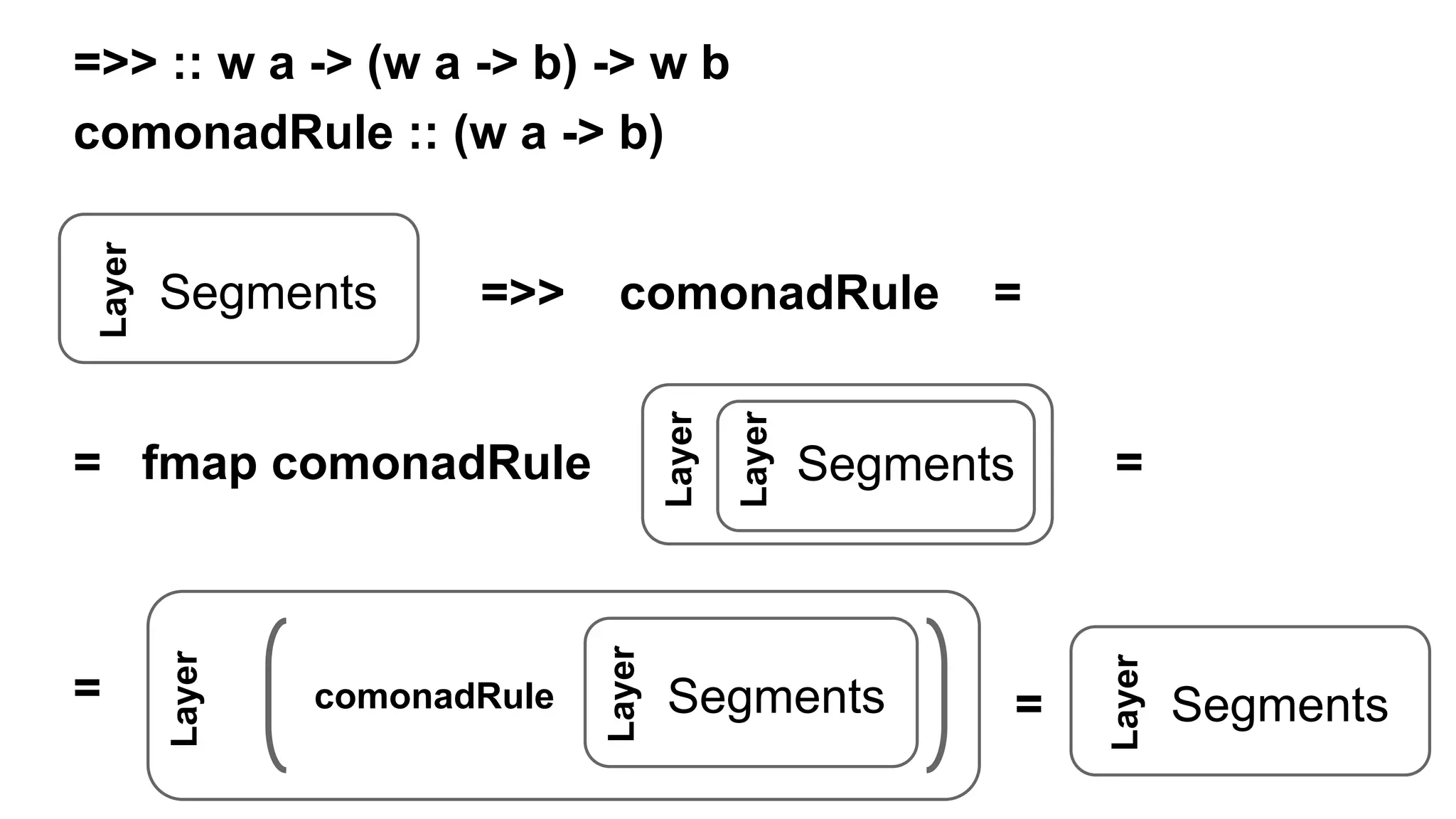
29. data Layer a = Layer a
comonadCantorRule :: Layer Segments -> Segments
comonadCantorRule layer = cantorGen (extract layer)
comonadCantorGen :: Layer Segments -> Layer Segments
comonadCantorGen layer = layer =>> comonadCantorRule
> take 2 $ iterate comonadCantorGen cantorLayer
[ Layer [(0.0,9.0)], Layer [(0.0,3.0),(6.0,9.0)] ]
Фрактал - список слоев

30. Определение комонады
class Functor w => Comonad w where
extract :: w a -> a
duplicate :: w a -> w (w a)
extend :: (w a -> b) -> w a -> w b
extend f = fmap f . duplicate
duplicate = extend id
(=>>) :: Comonad w => w a -> (w a -> b) -> w b
cx =>> rule = extend rule cx

31. Простейшая комонада Layer
data Layer a = Layer a
instance Functor Layer where
fmap f (Layer a) = Layer (f a)
instance Comonad Layer where
duplicate (Layer a) = Layer (Layer a) -- w a -> w (w a)
extract (Layer a) = a -- w a -> a

32. Layer
Segments
Layer
Segments
Layer
duplicate =
Layer
Segments Segmentsextract =
duplicate :: w a -> w (w a)
extract :: w a -> a

33. =
Layer
Segments
Layer
comonadRule =
Layer
Segments
Layer
Segments =>> comonadRule =
=>> :: w a -> (w a -> b) -> w b
comonadRule :: (w a -> b)
Layer
Segments
Layer
= fmap comonadRule =

34. Спасибо за внимание!
Александр Гранин
graninas@gmail.com

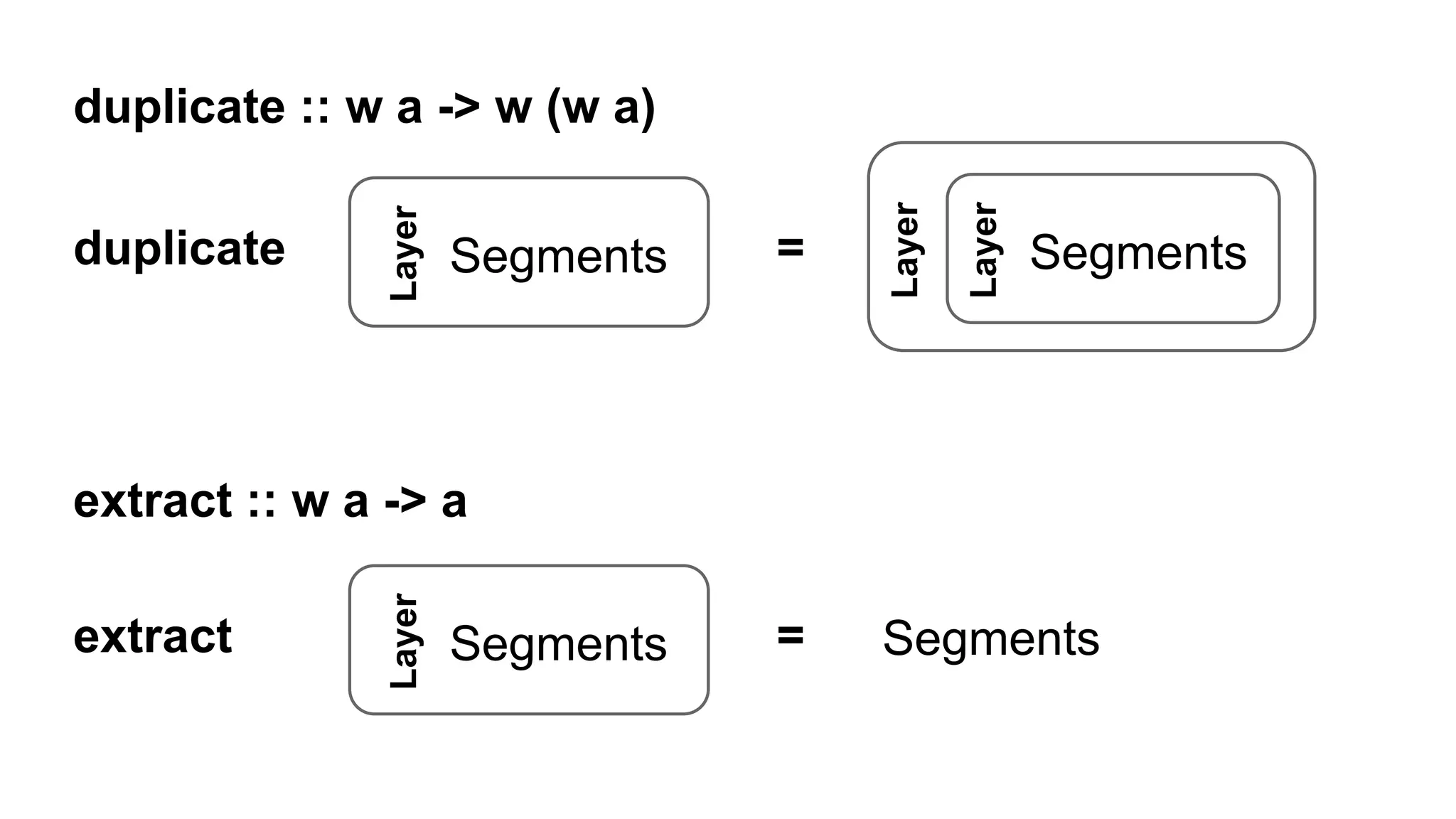
35. Зипперы - это комонады
http://habrahabr.ru/post/225473/
data Universe a = Universe [a] a [a]
left, right :: Universe a -> Universe a
left (Universe (a:as) x bs) = Universe as a (x:bs)
right (Universe as x (b:bs)) = Universe (x:as) b bs
extract :: Universe a -> a
extract (Universe _ x _) = x
duplicate :: Universe a -> Universe (Universe a)
duplicate u = Universe (tail $ iterate left u) u (tail $ iterate right u)

36. Зиппер зипперов чисел
universe = Universe [-1, -2..] 0 [1, 2..]
universeOfUniverses = duplicate universe
http://habrahabr.ru/post/225473/

37. 1
2
35
> goLeft (goRight zipper)
TZ (Node 5 Empty Empty)
[ LCtx 2 (Node 3 Empty Empty)
, RCtx 1 Empty]
RCtx 1
LCtx 2 3
5