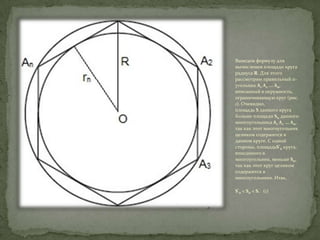
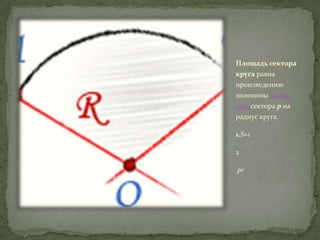
Документ описывает основные геометрические характеристики окружности, включая определения радиуса и диаметра, формулы для их вычисления, а также празднование дня числа π. Упоминаются даты, связанные с числом π, и приводится формула для вычисления площади круга. Также объясняется отношение между многоугольниками и окружностью при увеличении числа сторон.

1. КУШЕКОВ НАРИМАН

2. 2
Окружность — геометрическое место точек плоскости,
удалённых от некоторой точки — центра окружности —
на заданное расстояние, называемое радиусом
окружности.

3. Неофициальный праздник «День числа Пи» отмечается 14
марта, которое в американском формате дат (месяц/день)
записывается как 3.14, что соответствует приближённому
значению числа π.
Ещё одной датой, связанной с числом π, является 22 июля,
которое называется «Днём приближённого числа Пи», так
как в европейском формате дат этот день записывается
как 22/7, а значение этой дроби является приближённым
значением числа π.

4. 1
Диаметр можно найти по формуле: D = 2R, где диаметр равен удвоенному радиусу
окружности.
Радиус - расстояние от центра до любой точки окружности. Обозначается латинской R.
Если известен радиус окружности, допустим, он равен 8 см, то значит D = 2 * 8 = 16 см.

5. Радиус окружности: R = L/2π

6. Вторая формула, по которой можно найти диаметр окружности, выглядит так: D =
длину окружности поделить на Пи.
Число Пи применяется в математике для обозначения определённого
иррационального числа, и равно приблизительно 3,14.
Если известна длина окружности, допустим, 18 см, то значит D = 18 : 3,14 = 5,73 см

7. Вот так, оказывается, совсем несложно найти диаметр
окружности.

8. Напомним, что кругом называется часть плоскости, ограниченная
окружностью. Круг радиусаR с центром O содержит точку O и все
точки плоскости, находящиеся от точки O на расстоянии, не
большем R.

9. Будем теперь неограниченно увеличивать число сторон многоугольника.
,
где r n — радиус вписанной в многоугольник окружности. При
cos (180° / n) → 1, поэтому . Иными
словами, при неограниченном увеличении сторон многоугольника вписанная в него окружность
«стремится» к описанной окружности, поэтому при . Отсюда из неравенств (1) следует, что при . .

10. Выведем формулу для
вычисления площади круга
радиуса R. Для этого
рассмотрим правильный nугольник A1 A2 ... An,
вписанный в окружность,
ограничивающую круг (рис.
1). Очевидно,
площадь S данного круга
больше площади Sn данного
многоугольника A1 A2 ... An,
так как этот многоугольник
целиком содержится в
данном круге. С одной
стороны, площадьS'n круга,
вписанного в
многоугольник, меньше Sn,
так как этот круг целиком
содержится в
многоугольнике. Итак,
S'n < Sn < S. (1)

11. . По формуле S n = 1 / 2 P n r n ,
где P n — периметр многоугольника A 1 A 2 ... A n . Учитывая, что , , при ,
получаем . Итак, для вычисления площади S круга радиуса R мы
получили формулу S = πR 2

12. Площадь сектора
круга равна
произведению
половины длины
дугисектора p на
радиус круга.
1.S=1
2
pr

13. Площадь сегмента
круга,
окружностинаход
ится, как
разность площади
сектора AOBи площ
ади
равнобедренного
треугольникаAOB в
ыраженную через
угол
1.Sсегм= Sсект−Sтреуг