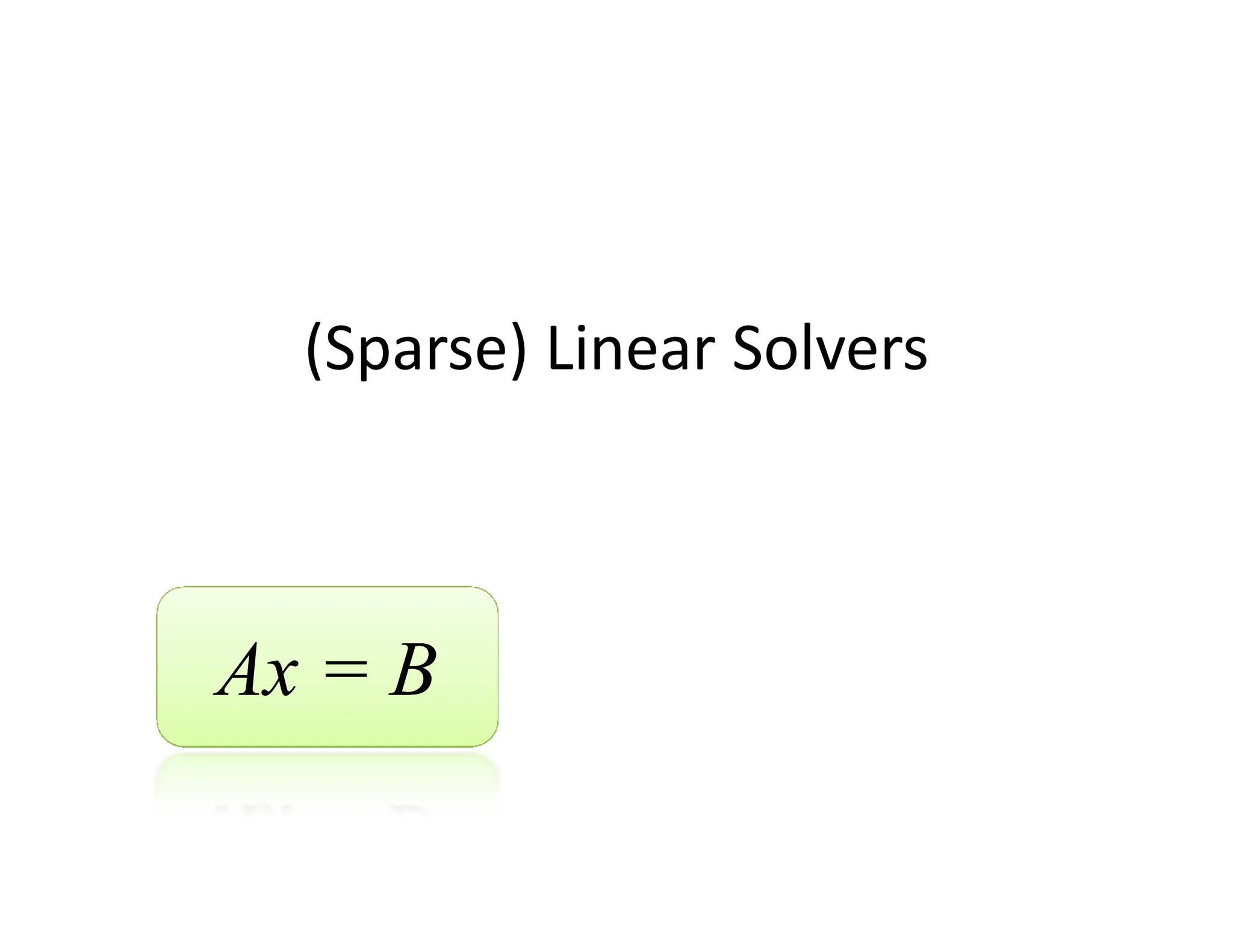
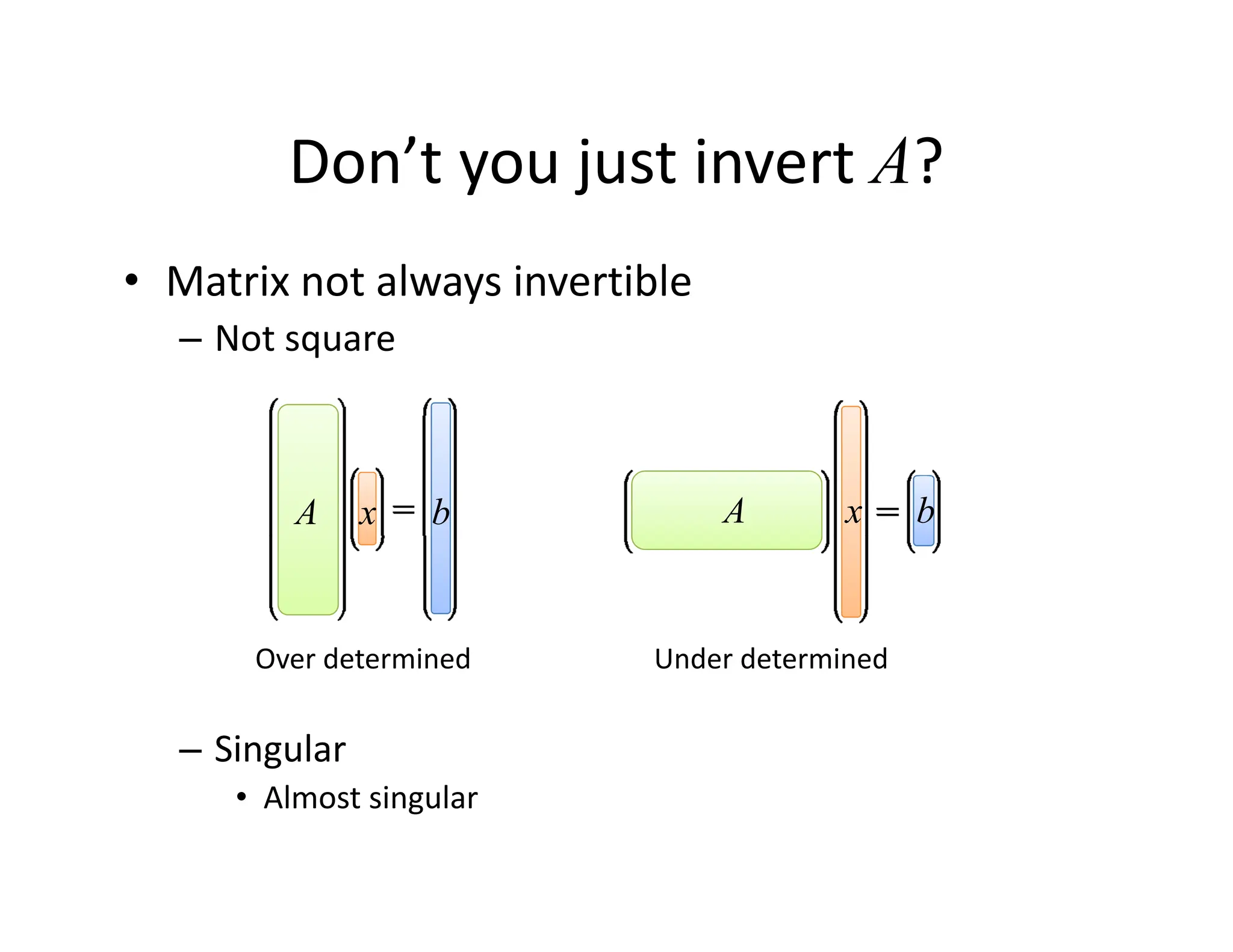
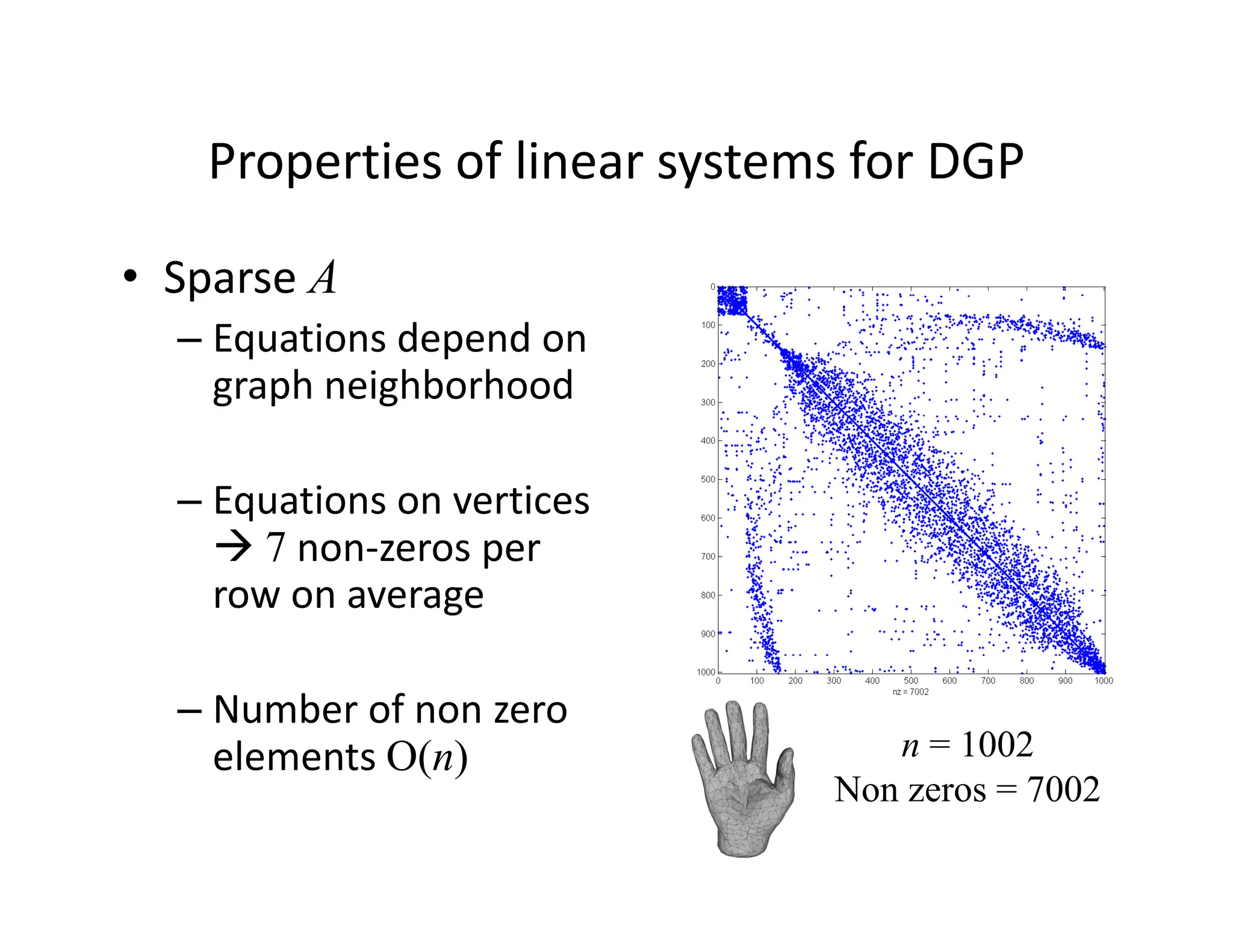
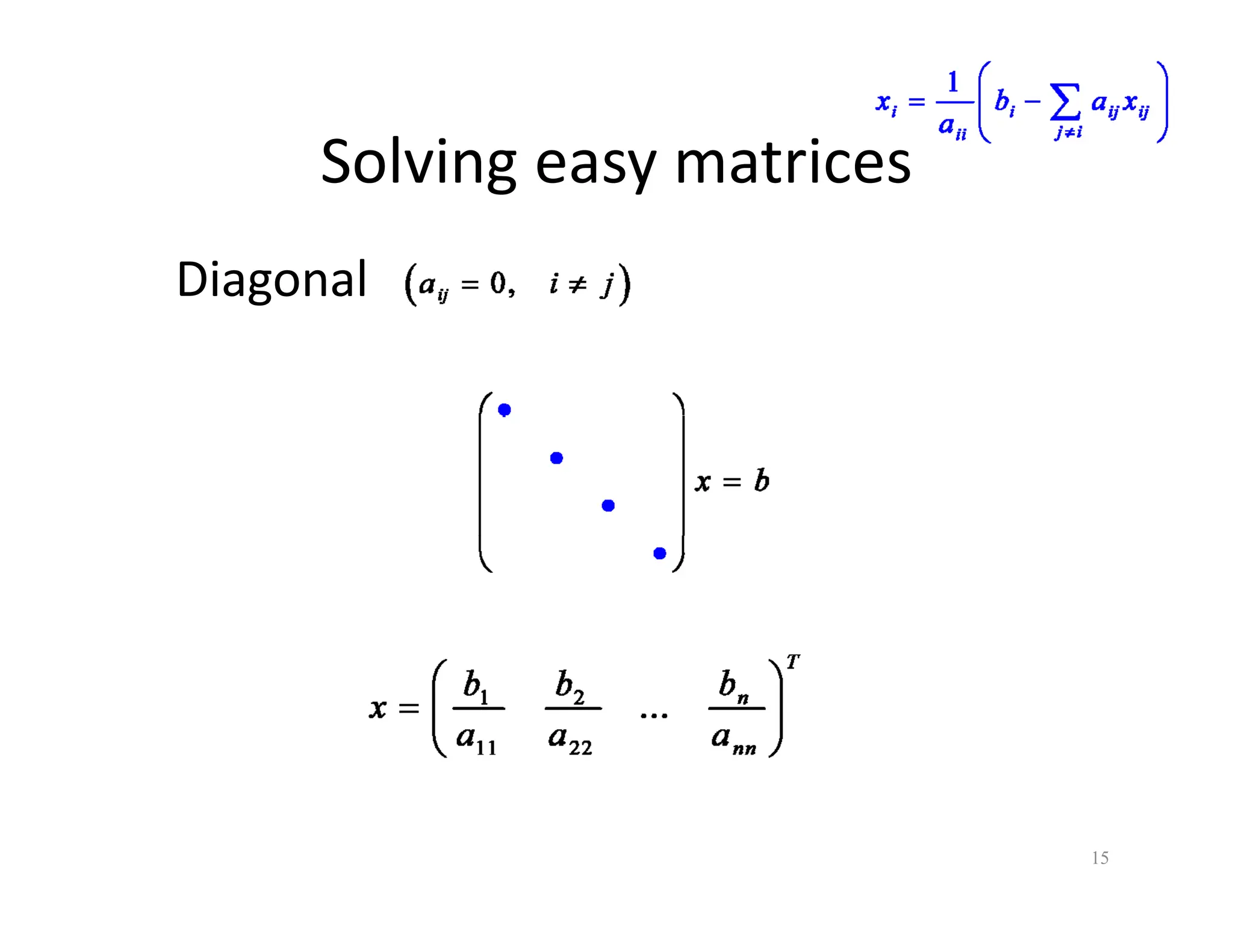
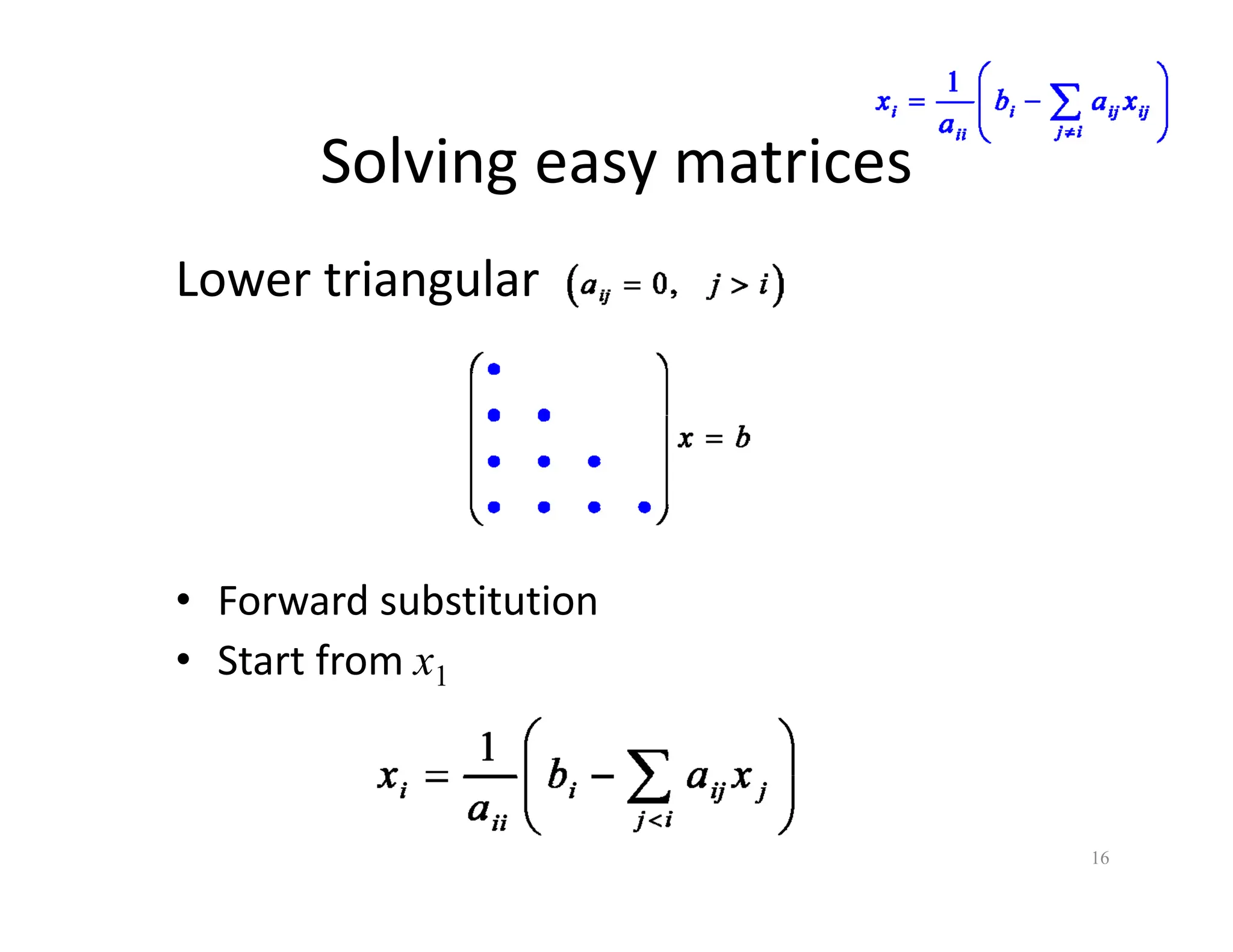
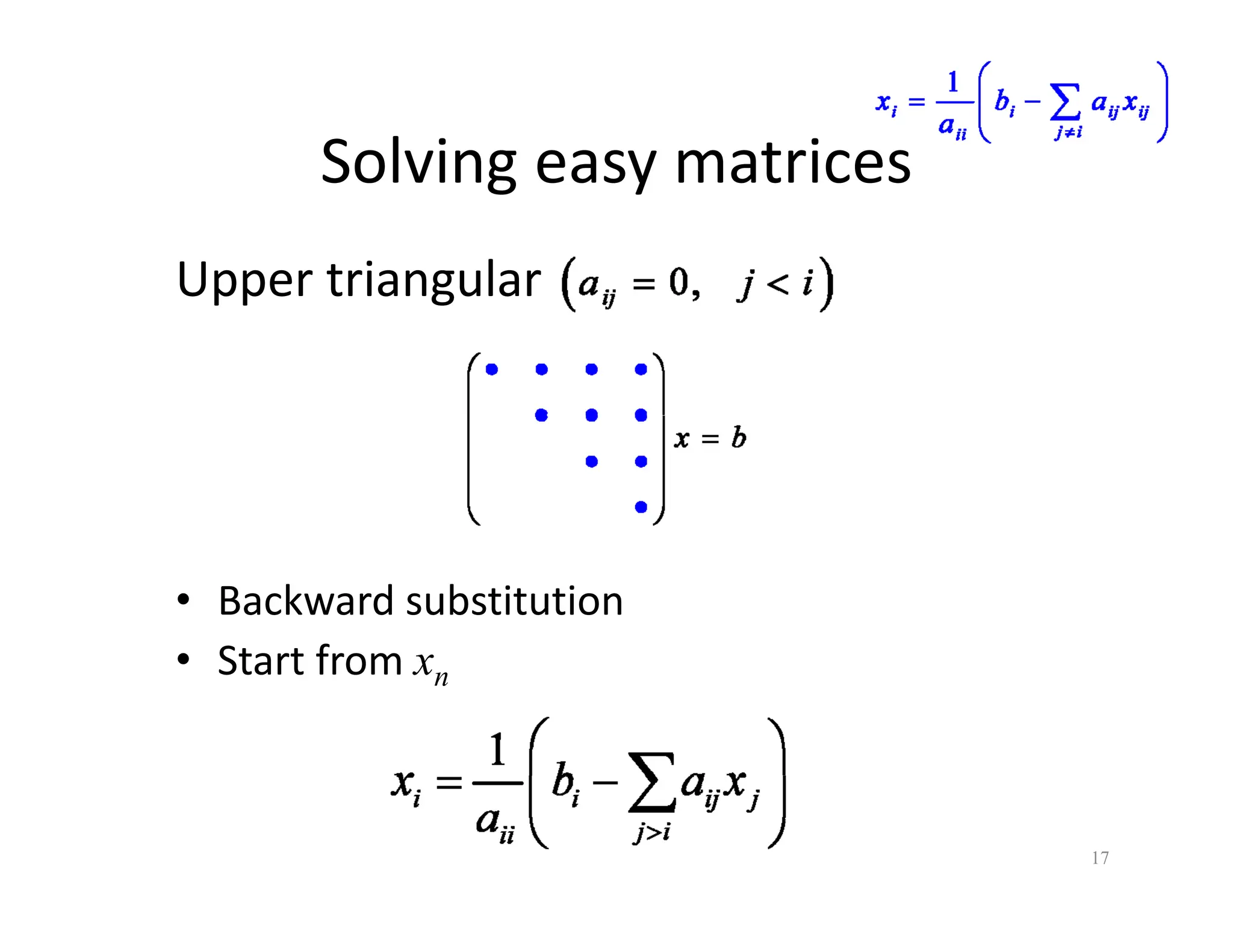
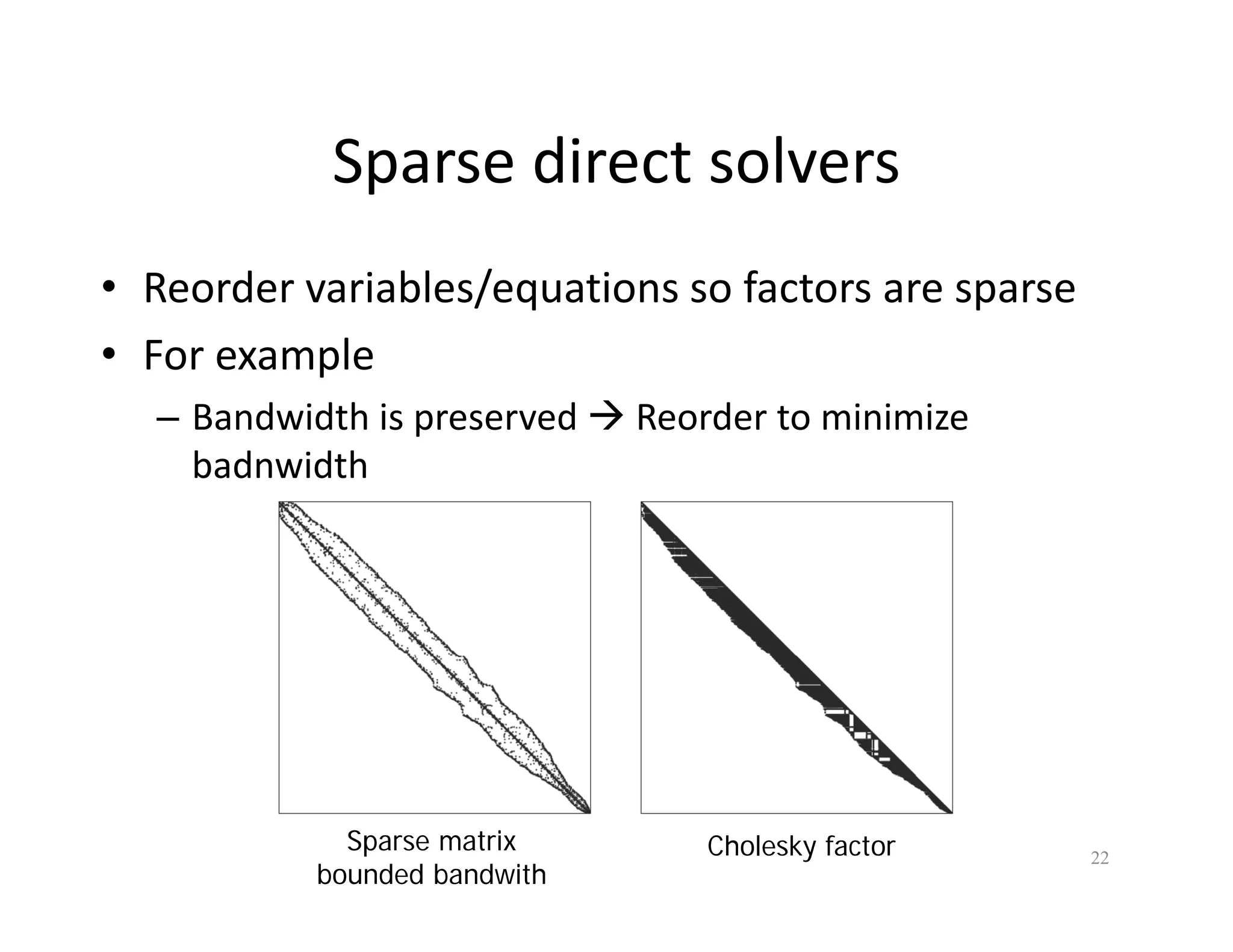
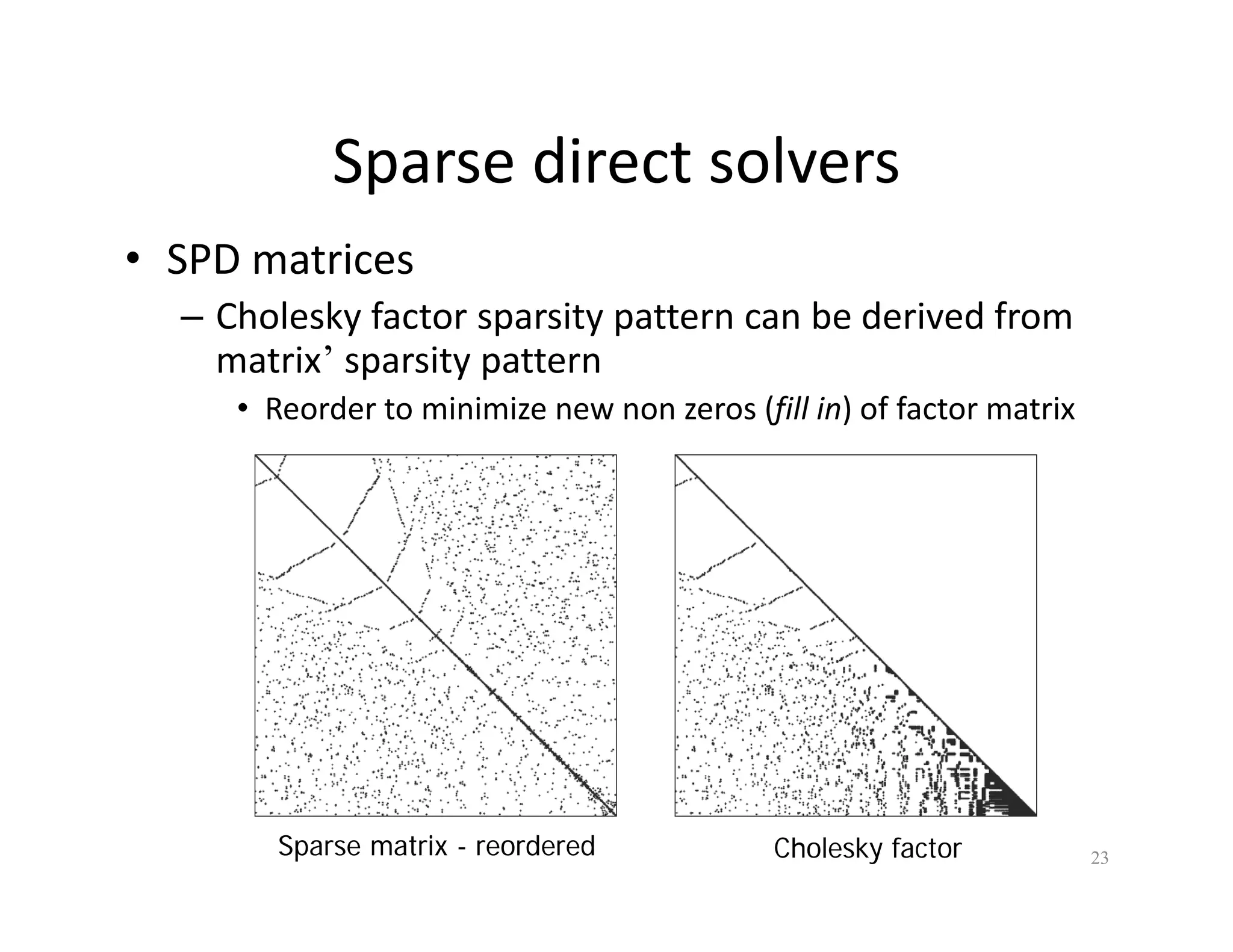
The document discusses various linear solvers useful for geometry processing applications, emphasizing the importance of solving linear systems defined by sparse matrices. It explains different types of solvers, including iterative and direct methods, outlining their respective advantages and disadvantages. The conclusions highlight that sparse solvers are often the best choice for sparse symmetric positive definite systems generated by geometry processing algorithms.