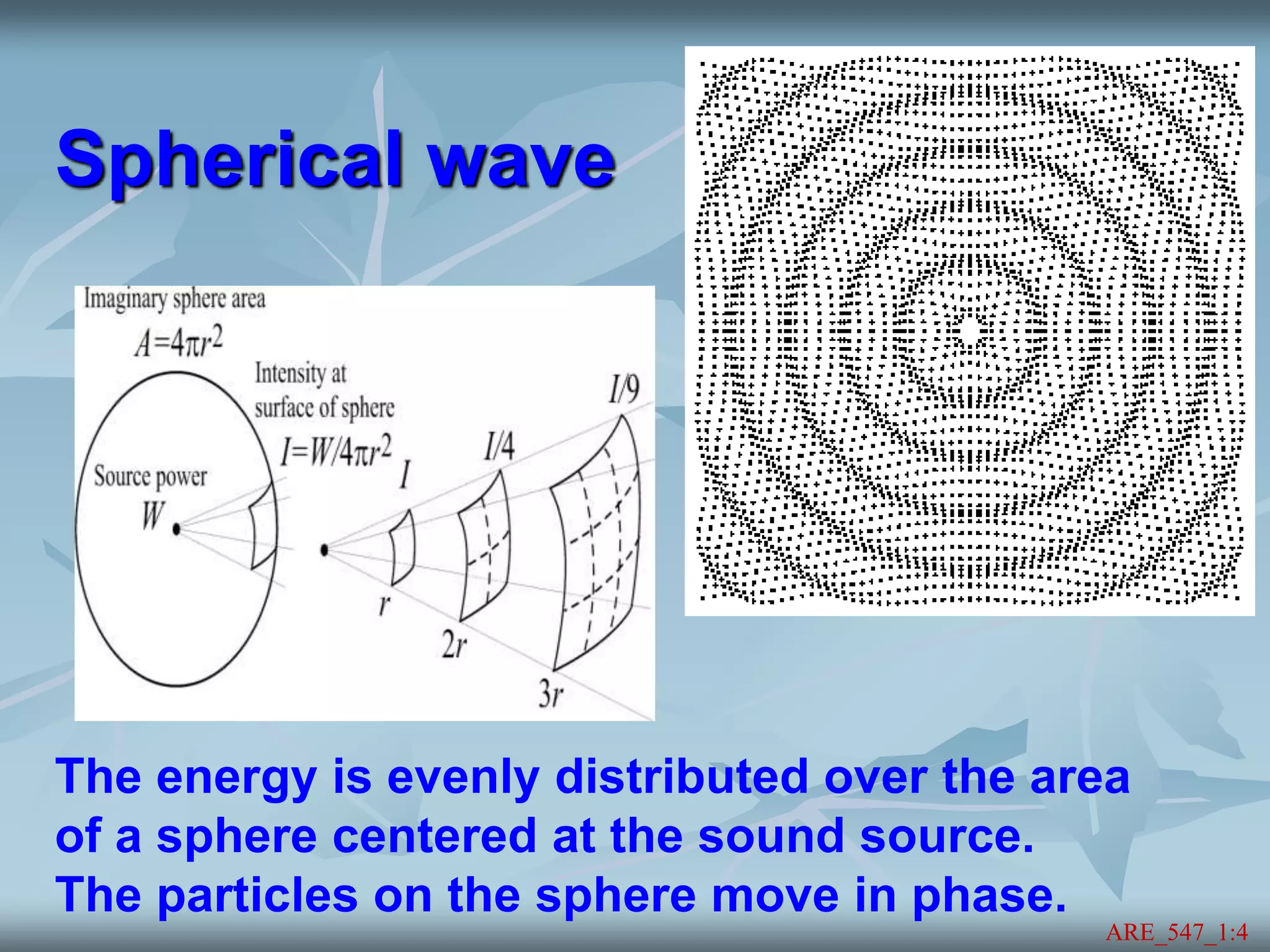
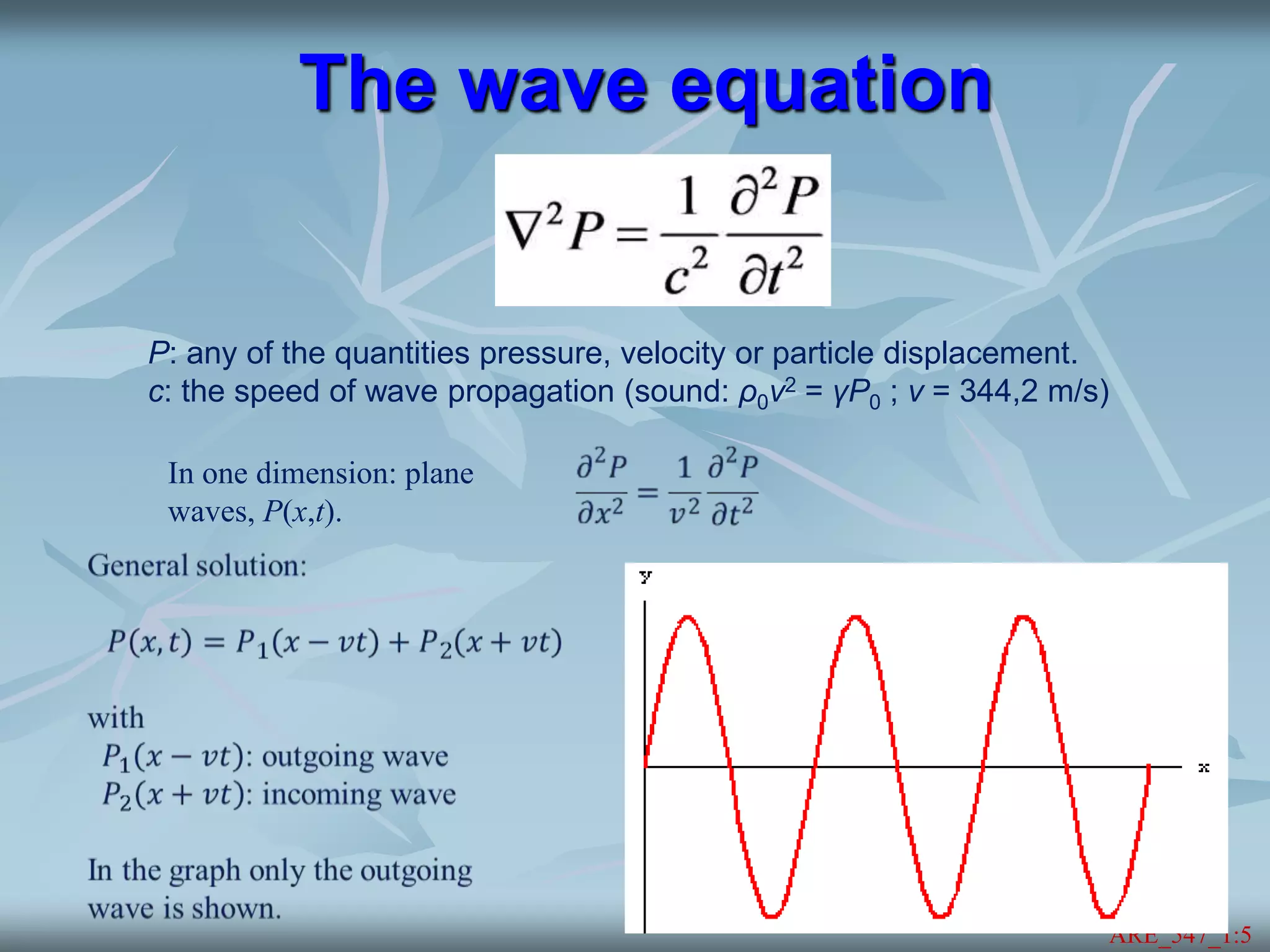
This document discusses the field of acoustics. It begins with definitions of acoustics and lists some of the main subfields, including physical acoustics, room acoustics, and building acoustics. Some pioneering figures in acoustics are mentioned, like Pythagoras, Vitruvius, and Helmholtz. The document then covers basics of sound waves, including propagation, reflection, refraction, diffraction, interference, and the Doppler effect. Key concepts discussed are the wave equation, standing waves, wavelength, frequency, and speed of sound in different media.

1. Building Acoustics
ARE 547
Dpt of Architectural Engineering
College of Environmental Design
KFUPM
Lecture 1
Djamel Ouis
2nd semester 2015
ARE_547_1

2. Acoustics
The science concerned with the
production, control, transmission,
reception, and effects of sound.
The science of sound and
vibrations.

3. Acoustics and its involvements:
Lindsay’s ”Wheel of Acoustics”
ARE_547_1:1

4. Acoustics: Sound and Vibrations
• Physical Acoustics: Wave propagation and vibrations
• Room Acoustics: sound within closed spaces
• Building Acoustics: Transmission of sound in
constructions
• Environmental Acoustics: road, train and air traffic,
industry
• Electroacoustics: Loudspeakers and Microphones
• Underwater Acoustics: Sonars and submarines
• Psychoacoustics: Hearing perception
• Speech and hearing
• Non-linear Acoustics: loud explosions
• Medical and chemical: ultrasounics
ARE_547_1:2

5. Acoustics
The oldest branch of “Natural Philosophy”?
In the 6th Century BC, the ancient
Greek philosopher Pythagoras wanted
to know why some combinations of
musical sounds seemed more beautiful
than others, and he found answers in
terms of numerical ratios representing
the harmonic overtone series on a string.
He is reputed to have observed that
when the lengths of vibrating strings
are expressible as ratios of integers (e.g. 2 to 3, 3 to 4), the
tones produced will be harmonious, and the smaller the
integers the more harmonious the sounds.

6. Acoustics
Vitruvius (80/70-15 BC), Roman architect: father of
architectural acoustics, used bronze vessels to control
reverberation (echeia). He made accurate description
of their placement, number, and tuning; desirable for
music but not always for speech.
Gallilei (1564-1642) and French mathematician Marin Mersenne
(1588-1648) studied the vibration of stretched strings, and found
the complete laws of their vibrations.
Colladon and Sturm measured in 1826,
Lake Geneva, the speed of sound in water:
1437 m/s (today’s: 1481 m/s, 3% error)

7. Acoustics; some great names
H. von Helmholtz
(1821-94)
On the Sensations
of Tone (1863)
Lord Rayleigh
(1842-1919)
The Theory of
Sound (1877)
Collected Papers
on Acoustics (1923)
J. W. Sabine
(1868-1919)

8. Basics of Sound
 Sound is the result of propagation of a perturbation in a
medium: No sound in a vacuum.
 A sound wave is a longitudinal wave: the particle motion
is in the direction of propagation of the wave (cf EM wave)
ARE_547_1:3
A transversal wave, here a seismic wave
(Rayleigh surface wave): The particles at the
surface move along an elliptical pathway.

9. Spherical wave
The energy is evenly distributed over the area
of a sphere centered at the sound source.
The particles on the sphere move in phase.
ARE_547_1:4

10. The wave equation
ARE_547_1:5
P: any of the quantities pressure, velocity or particle displacement.
c: the speed of wave propagation (sound: ρ0v2 = γP0 ; v = 344,2 m/s)
In one dimension: plane
waves, P(x,t).

11. A standing wave
Example of a sound wave in a
closed tube
Superposition of 2 waves
traveling in opposite directions
Red wave: moving right,
Green wave: moving left
Blue wave: sum of the two;
a standing wave
ARE_547_1:6

12. Period, frequency and wavelength
ARE_547_1:7
A (harmonic) wave (often) has a double periodicity:
in space (wavelength: l), and in time (period: T)
f
v
Tv l
vair= 340 m/s
vwater= 1400 m/s
vsteel= 5400 m/s

13. Wave propagation phenomena:
Reflection
Reflection law: The angle of
reflection is equal to the angle
of incidence: θi= θr
String held fixed at one
end: Reflection with
phase shift (180o).
Hard boundary
String with free end:
Reflection with no
phase shift.
Soft boundary
ARE_547_1:8

14. Wave propagation phenomena:
Refraction
ARE_547_1:9
Change of the direction of
propagation due to a change in
the wave propagation speed.
e.g. wind gradient or
temperature gradient
Medium with lower speed => shorter
wavelength
f
v
l

15. Wave propagation phenomena:
Diffraction
 Diffraction occurs whenever a wave encounters
an obstacle: The wavefront is influenced.
ARE_547_1:10
From a plane wave to a
spherical wave.
The wavefronts get less deformed for
a wider gap.

16. Diffraction
ARE_547_1:11
Barrier height: λ Barrier height: 2 λ Barrier height: 4 λ
Diffraction is a low frequency phenomenon:
Wave proceeds indisturbed for obstacles of the size << λ.
We can hear, but not see around a corner!
Interference: here with two sources. Both
interference and diffraction are involved.
Principle of superposition:
The effect of a sum of causes is equal to
the sum of the effects of each cause.

17. Wave superposition
Beats, amplitude modulation, AM
 Superposition of two harmonic signals with nearby
frequencies. Adjusting musical instruments (piano &
pitch fork)
ARE_547_1:12

18. The Doppler Effect
The moving sound source
ARE_547_1:13
Stationary sound source Moving sound source
Change of frequency (pitch):