Solution 3 3

Classical Mechanics Homework 2
Due October 12, 2012

1. (Taylor, Problem 2-11) Consider an object that is thrown vertically up
with initial speed v0 in a linear medium.
StatementThis is another problem in which we consider the effects of air
resistance on motion under gravity. In this case we need to find the height
as a function of time going up, starting with some initial velocity.
AssumptionsWe assume linear drag plus gravity, and linear motion. The
object is a point particle.
Physical representationThe forces we need are gravity pointing down,
hence negative, and drag pointing down, also negative. We consider mo-
tion going up only, and do not worry what happens after we reach the top
of the orbit.
Mathematical representation and solutionMathematical representa-
tion and solution, see parts below.

(a) Measuring y upward from the point of release, write expressions for
the object’s velocity vy (t) and position y(t).
This follows exactly what we did in class. Starting with an expression
for Newton’s 2nd Law (coordinate system positive upward):

mv
˙ = −mg − bv
∫ v ∫ t
m
dv ′ = − dt′
v0 mg + bv ′ 0
( )
m mg + bv
− ln = t
b mg + bv0
( mg ) mg
v = + v0 e−bt/m −
b b
Now, separate again to find position as a function of time:
∫ y ∫ t [( )
′ mg ′ mg ] ′
dy = + v0 e−bt /m − dt
y0 0 b b

m ( mg )( ) mg
y − y0 = + v0 1 − e−bt/m − t
b b b

(b) Find the time for the object to reach its highest point and its position
ymax at that point.

The highest point occurs when the velocity goes to zero:
( )
m mg + bv
t = − ln
b mg + bv0
( )
m mg
tmax = − ln
b mg + bv0
( )
m mg + bv0
= ln
b mg
Finding the height at this time:
−b −m
( mg )
e−btmax /m = e m b
ln mg+bv
0

mg
=
mg + bv0

m ( mg )( mg
)
m2 g
(
mg + bv0
)
ymax − y0 = + v0 1− − 2 ln
b b mg + bv0 b mg

mg bv0
1− =
mg + bv0 mg + bv0
( )
m ( mg ) v0 m2 g mg + bv0
ymax − y0 = + v0 ( mg ) − 2 ln
b b b + v0
b mg

( )
m m2 g mg + bv0
ymax − y0 = v0 − 2 ln
b b mg

(c) Show that as the drag coeﬃcient approaches zero, your last answer
2
reduces to the well known result ymax = 1/2 v0 /g for an object in
vacuum. [Hint: If the drag force is very small, the terminal speed is
very big, so v0 /vterm is very small. Use the Taylor series for the log
function to approximate ln (1 + δ) by δ − 1 δ 2 .
2
Now, recognizing that b is small:
( ) ( )
mg + bv0 bv0
ln = ln 1 +
mg mg

bv0 1 (bv0 )2
≈ −
mg 2 (mg)2

So, the maximum height becomes:
( )
m m2 g bv0 1 (bv0 )2
ymax − y0 ≈ v0 − 2 −
b b mg 2 (mg)2

2
m m 1 v0
= v0 − v0 +
b b 2 g
2
1 v0
ymax − y0 ≈
2 g
So, the power series approximation of the maximum height in drag
case reduces to the non-drag case when the drag coefficient is small
(as it should).
Evaluation The equation we found for y(t) had the same form as the
equation we had in class, so that sounds right. There is a term linear
in time going down, representing the terminal velocity, and an exponen-
tial approach to this terminal velocity. The formula gives us a maximum
height, which in the limit of small drag gives the standard result. We could
also check to see that the maximum height is actually less than the maxi-
mum height without drag! Finally, for linear motion the equation is valid
for all directions of the motion, so we can use the same equation for going
down!
2. (Thorton & Marion, Problem 2-15) A particle of mass m slides down an
inclined plane under the influence of gravity. If the motion is resisted by
a force f = kmv 2 , show that the time required to move a distance d after
starting from rest is:

cosh−1 ekd
t= √
kg sin θ
where θ is the angle of inclination of the plane.
StatementThis problem is a variation on the well known inclined plane
problem. We add friction and are asked to evaluate distance versus time.
The equations are more complicated then those we had in Ph211.
AssumptionsWe assume we have a point particle, with gravity, and that
the friction force is quadratic. We included the mass as a second factor
in the model for friction, the guess is that this will make the equations
somewhat more simple.
Physical representationThis is a problem with motion in one dimen-
sion, one degree of freedom, so we use a coordinate system that reflects
this. Taking the x-axis along the plane of the incline seems reasonable.
We take x positive in the down direction. The set-up of the problem is a
second law problem, F=ma, which we need to solve.
I’ll use a coordinate system where the coordinate x is parallel to the in-
clined plane. The component of the net force parallel to the incline is:
ΣFx = mvx = mg sin θ − kmv 2
⃗ ˙

mdv ′
= dt′
mg sin(θ) − kmv ′ 2
Note that as usual the mass of the object drops out! Gravity and acceler-
ation always contain mass in the same manner.
dv ′
= dt′
g sin(θ) − kv ′ 2
Integrating:
∫ ∫
v
dv ′ t
= dt′
0 g sin θ − kv ′ 2 0

∫ ∫
1 v
dv ′ t
− = dt′
k 0 v ′ − c2
2
0
where we have deﬁned
g
sin(θ) c2 =
k
∫ v[ ] ∫ t
1 dv ′ dv ′
− − ′ = dt′
2ck 0 v ′ − c v + c 0
1
−
[ln(|v − c|) − ln(c) − ln(v + c) + ln(c)] = t
2ck
We know that we have v < c, we never reach terminal velocity. Therefore
c−v
ln( ) = −2ckt
c+v
Solve for v so that I can ﬁnd the distance:

(c − v) = (c + v)e−2ckt

v(1 + e−2ckt ) = c(1 − e−2ckt )
1 − e−2ckt
v=c
1 + e−2ckt
√ (√ )
g sin θ
v = tanh t kg sin θ
k
∫ d ∫ t √ ( √ )
g sin θ
dx′ = tanh t′ kg sin θ dt′
0 0 k
√ [ ( √ )]
g sin θ 1 t
d = √ ln cosh t′ kg sin θ
k kg sin θ 0

1 [ (√ )]
d = ln cosh t kg sin θ
k

Solving for t:
(√ )
ekd = cosh t kg sin θ

cosh−1 ekd
t = √
kg sin θ
This part of the question was not asked, but is a useful example. Using:
2
k = 0.5 N/(m/s)
π
θ = radians
3

0.7

0.6

0.5

Time, t [s] 0.4

0.3

0.2

0.1

0
0 0.5 1.0 1.5 2.0
Distance , d m
Quadratic Drag No Drag

For the no drag case: √
2d
t=
g sin θ
The plot shows that the no drag case reaches a larger distance in the same
amount of time.
Evaluation In order to make sense of the results we do have to look at
the extra parts. With friction we travel a smaller distance than without,
which is expected. Also, in the limit of zero friction we have from
1 − e−2ckt
v=c
1 + e−2ckt
that
2ckt
v≈c = c2 kt
1+1

, or
v = g sin(θ)t
as expected.

3. (Taylor, Problem 2-55) A charged particle of mass m and positive charge q
moves in uniform electric and magnetic fields, E pointing in the y-direction
and B in the z-direction (an arrangement called “crossed E and B fields”).
Suppose the particle is initially at the origin and is given a kick at time
t = 0 along the x-axis with vx = vx0 (positive or negative).
Statement This is an example of a two-dimensional problem, with a ve-
locity dependent force. Hence the directions of the force are complicated,
even though the magnitudes are not.
AssumptionsWe assume a point particle. The total force is a combina-
tion of the electric and magnetic force.
Physical representationWe need to write a two dimensional form of
F=ma. The forces are given by the Lorentz force. The velocities are given
by vx and vy , the components of the velocity, and these components can
be negative. It is easiest to work in Carthesian coordinates.

(a) Write down the equation of motion for the particle and resolve it
into its three components. Show that the motion remains in the
plane z = 0
Starting with Newton’s Second Law:

ΣF = mv = q(E + v × B)
˙

Looking at each of the fields:

E = E0 ˆ
j
v × B = vy B 0 ˆ − vx B 0 ȷ
ı ˆ

So, the equations of motion become:
qB0
vx
˙ = vy
m
q
vy
˙ = (E0 − B0 vx )
m

(b) Prove that there is a unique value of vx0 , called the drift speed ddr ,
for which the particle moves undeflected through the fields. (This is

the basis of velocity selectors, which select particles traveling at one
chosen speed from a beam with many different speeds.)
For there to be no deflection, the force in the y-direction must be
zero.

ΣFy = q(E0 − B0 vx )

0 = q(E0 − B0 vx )

E0
vx =
B0

E0
vdr =
B0

(c) Solve the equations of motion to give the particle’s velocity as a
function of t, for arbitrary values of vx0 . [Hint: The equations for
(vx , vy ) should look very much like Equations (2.86) except for an
offset of vx by a constant. If you make a change of variables of the
form ux = vx − vdr and uy = vy , the equations for (ux , uy ) will have
exactly the form (2.68), whose general solution you know.]
Letting

ux = vx − vdr

uy = vy

The equations of motion become:
qB0
ux
˙ = uy
m
qB0
uy
˙ = − ux
m

Taking another time derivative of the x equation yields:
qB0
ux =
¨ uy
˙
m

Now, substituting the original equation of motion:
qB0
ux
¨ = − ux
m
ux = A sin ω t + B cos ω t

vx = A sin ω t + B cos ω t + vdr

qB0
where ω = m This gives
u˙x = Aω cos(ωt) − Bω sin(ωt)
qB0
uy = Aω cos(ωt) − Bω sin(ωt)
m
Using the initial condition that uy (t = 0) = 0 gives A = 0. Using the
initial condition that vx (t = 0) = vx0 :
vx0 = B + vdr

B = vx0 − vdr

vx = (vx0 − vdr ) cos ω t + vdr

Now, using this result to ﬁnd the vy
qB0
uy
˙ = − ux
m
qB0
vy
˙ = − (vx − vdr )
m
qB0
vy
˙ = − (vx0 − vdr ) cos ω t
m
∫ vy ∫ t
′
dvy = −ω(vx0 − vdr ) cos ω t′ dt′
0 0

vy = −(vx0 − vdr ) sin ω t

(d) Integrate the velocity to ﬁnd the position as a function of t and sketch
the trajectory for various values of vx0
The integration is straightforward:
vx = (vx0 − vdr ) cos (ω t) + vdr
∫ x ∫ t
dx′ = [(vx0 − vdr ) cos (ω t′ ) + vdr ] dt′
x0 0

[ ] t
vx0 − vdr
x − x0 = sin (ω t′ ) + vdr t′
ω 0

vx0 − vdr
x − x0 = sin (ω t) + vdr t
ω

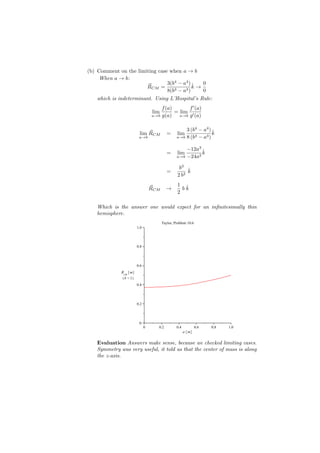
vy = −(vx0 − vdr ) sin (ω t)
∫ y ∫ t
′
dy = − (vx0 − vdr ) sin (ω t′ ) dt′
y0 0

t
vx0 − vdr
y − y0 = cos (ω t′ )
ω 0

vx0 − vdr
y − y0 = [cos (ω t) − 1]
ω
Trajectories can be oscillatory or run back.

0.0 2.5 5.0 7.5 10.0 12.5
0.0

−0.5

−1.0

−1.5

−2.0

Evaluation We found several familiar results. The condition for no de-
flection was found in Ph213, as was the cyclotron frequency. We can
also set the electric field equal to zero, which gives vdr = 0 and the orbit
becomes a circle as expected.
4. (Thorton & Marion, Problem 9-60) A rocket has an initial mass of 7 × 104
kg and on firing burns its fuel at a rate of 250 kg/s. The exhaust velocity
is 2500 m/s. If the rocket has a vertical ascent from rest on the earth, how
long after the rocket engines fire will the rocket lift off? What is wrong
with the design of this rocket?
StatementAn application of what we did in class, but now using realistic
numbers. We are asked about the conditions for lift-off for a rocket, and
need to check if the thrust is strong enough.
AssumptionsThe fuel is spent at a constant rate, and we do not take
into account how the exhaust gas hits the launch pad.

Physical representationWe choose dm negative, which makes sense
from a mathematical perspective. We use the equation of motion for the
center of mass to get a simple formula. Momentum is changing because
gravity is acting.
The rocket will lift oﬀ when the acceleration is positive. From the equation
for the motion of the center of mass in the book we have

dP = mdv + vex dm = −mgdt

and we need a positive value of dv, or

|dm|vex > mgdt

or
dm
|
|vex > mg
dt
We’re given that m = constant = −250 kg/s, vex = 2500 m/s. This
˙
implies
9.8m < (250)(2500)
m < 63.8 × 103 kg
But m0 = 7 × 104 kg. Hence we need to lose 6, 200 kg before we can take
oﬀ. At the rate we have here that takes 24.8 seconds!
Evaluation This is a long time to be sitting on the launch pad. Either
the rocket should be made lighter (perhaps by including less fuel, or by
constructing it out of lighter materials) or the thrust should be bigger (by
increasing the relative velocity of the rocket and the exhaust or by increas-
ing the fuel burn rate m.
˙

30

20

t [s]
liftoff

10

K K K K
0

280 270 260 250

dm kg
dt s

5. (Taylor, Problem 10.6) Find the CM of a uniform hemispherical shell of
inner and outer radii a and b and mass M .
Statement This problem asks us to evaluate the center of mass.
AssumptionsWe have a hemispherical shell with constant mass density.
Physical representationThis problem seems like it works best with spher-
ical coordinates. We take the x and y axis along the plane of the cut, and
have the z-axis pointing upwards through the hemisphere. This represen-
tations makes full use of the symmetry of the problem.
I’m going to place my origin of coordinates at the center of the sphere.
Using spherical coordinates:
∫
1
⃗
RCM = ρ(⃗′ ) ⃗′ dτ ′
r r
M
∫ ∫ ∫
1
ρ(⃗′ ) ⃗′ r′ dr′ sinθ dϕ′ dθ′
2
= r r
M

⃗
r ˆ
= r cos ϕ sin θˆ + r sin ϕ sin θˆ + r cos θk
ı ȷ

ρ(⃗′ ) =
r ρ
∫ π/2 ∫ 2π ∫ b [ ]
ρ
⃗
RCM = r′ cos ϕ′ sin θ′ˆ + r′ sin ϕ′ sin θ′ ȷ + r′ cos θ′ k r′ sinθ dr′ dϕ′ dθ′
ı ˆ ˆ 2
M 0 0 a

Considering each component separately:
∫ π/2 ∫ 2π ∫ b
ρ
r′ cos ϕ′ sin θ′ˆr′ sinθ dr′ dϕ′ dθ′
2
Rx = ˆ
ı ı
M 0 0 a

In performing the ϕ integral, since I’m integrating over a full period, the
integral goes to zero. This is true for Ry too. So:

Rx = 0

Ry = 0

∫ π/2 ∫ 2π ∫ b
ρ ˆ
r′ cos θ′ r′ sinθ dr′ dϕ′ dθ′
2
Rz = k
M 0 0 a

( b
)∫
π/2
ρ r4
= 2π sin θ′ cos θ′ dθ′
M 4 a 0

let u = sin θ′ so du = cos θ′ dθ′ , then:
( )∫ 1
ρ b4 − a4
Rz = 2π u du
M 4 0

( )
ρ b4 − a4 1
= 2π
M 4 2

As expected, RCM lies on the z-axis (expected because of symmetry). Now,
substituting in for the density:
M M 3M
ρ= = =
V (4/3)π(b3 −a3 ) 2π(b3 − a3 )
2

⃗ 3 b4 − a4 ˆ
RCM = k
8 b3 − a3

(a) Comment on the limiting case when a → 0.
When a → 0:
3(b4 − a4 ) ˆ 3 ˆ
⃗
RCM = 3 − a3 )
k→ bk
8(b 8
Which is the center of mass for a hemisphere of radius b.

(b) Comment on the limiting case when a → b
When a → b:
3(b4 − a4 ) ˆ 0
⃗
RCM = k→
8(b3 − a3 ) 0
which is indeterminant. Using L’Hospital’s Rule:
f (a) f ′ (a)
lim = lim ′
a→b g(a) a→b g (a)

⃗ 3 (b4 − a4 ) ˆ
lim RCM = lim k
a→b a→b 8 (b3 − a3 )

−12a3 ˆ
= lim k
a→b −24a2

b3 ˆ
= k
2 b2
1 ˆ
⃗
RCM → bk
2

Which is the answer one would expect for an inﬁnitesimally thin
hemisphere.
Taylor, Problem 10.6
1.0

0.8

0.6
Rcm m
b =1
0.4

0.2

0
0 0.2 0.4 0.6 0.8 1.0
a m

Evaluation Answers make sense, because we checked limiting cases.
Symmetry was very useful, it told us that the center of mass is along
the z-axis.

Solution 3 3

More Related Content

Similar to Solution 3 3

More from usepnuh

Solution 3 3