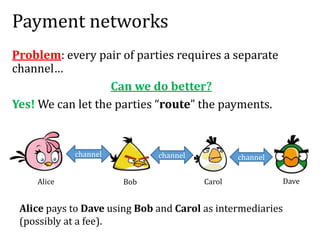
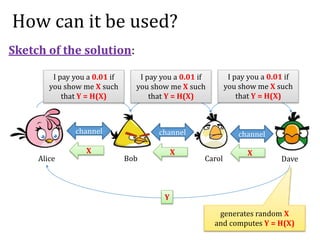
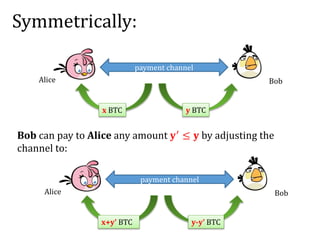
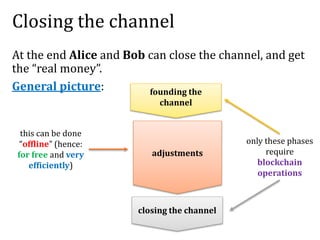
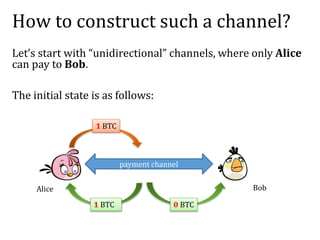
The document provides an introduction to smart contracts and scripting in Bitcoin, explaining how transactions can be structured through conditions and signatures. It discusses challenges such as micropayments and introduces payment channels, allowing for off-chain transactions to avoid high fees and delays. Additionally, it outlines the use of hash-locked transactions and improvements brought by the Lightning Network to enhance transaction efficiency.

1. Smart Contracts and Applications
(part I)
Stefan Dziembowski
University of Warsaw
Workshop on Bitcoin, Introduction to Cryptocurrencies,
Kfar Maccabiah, Ramat Gan, Israel, June 6-7, 2016

2. This lecture
We give a short introduction to the smart
contracts and the scripting features of
Bitcoin

3. Strange transactions:
T2 = (User P1 sends 1 BTC from T1 to P2 signature of P1 on [T2])
T3 = (User P2 sends 1 BTC from T2 to P3 signature of P2 on [T3])
P2
P3
T2 = a condition C2 to spend T2 a “witness W2”
T3 = a “witness W3”
P2
P3
T1
1
BTC
T2
1
BTC a condition C3 to spend T3
a Boolean function
Standard transactions:

4. Redeeming condition
T3 redeems T2 if
C2 evaluates to true on input ([T3],W3).
Note: in the the standard transactions:
C2([T3],W3) = Vrfy(pk2,[T3],W3)
[T3]
T2 = a condition C2 to spend T2 a “witness W2”
T3 = a “witness W3”
P2
P3
T1
1
BTC
T2
1
BTC a condition C3 to spend T2

5. Example: “Alice gives 1 BTC to the Bob if
he factors 2501.”
T2 =
can be spent using Bob’s
signature and p and q
such that p,q > 1
and pq = 2501
Alice’s
signature
T1
1
BTC
T3 =
can be spent using
Bob’s signature
p=41
q=61
Bob’s
signature
on [T3]
T2
1
BTC
Alice posts:
T1 --- earlier transaction that can be spent by Alice
Bob claims the
money by
posting:
formally:
C([T],(p,q,𝝈)) = true iff
p,q>1 & pq=2501
and 𝝈 is Bob’s signature on [T]

6. How are the conditions written?
In Bitcoin scripting language (non-Turing
complete stack-based)
Example:
OP_DUP OP_HASH160
02192cfd7508be5c2e6ce9f1b6312b7f268476d2
OP_EQUALVERIFY OP_CHECKSIG

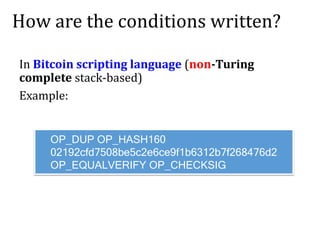
7. Bitcoin contracts
The “strange transactions” can be used to create the “Bitcoin
contracts”.
Simple examples:
• Payment channels
• Pay money to anyone who knows some password.
• Assurance contracts.
• Put a “deposit” to prove you are not a spammer.
• Pay money only if some event happens (may require an oracle).
More advanced examples:
• ‘’decentralized organizations”
• secure multiparty computation protocols [Andrychowicz, D.,
Malinowski, Mazurek, 2014, Bentov and Kumaresan 2014].

8. Payment channels

9. A problem with Bitcoin
It’s hard to do micropaments in Bitcoin.
Reasons:
• non-negligible transactions fees
• long transaction confirmation times
Inherent limitation of Bitcoin: 7 transactions/second.
paymements worth a fraction of a cent

10. A way to deal with this problem
Payment channels (e.g. the Lightning Network).
Alice and Bob establish a channel that allows them to
do transactions without posting them on the
blockchain.
Alice Bob
payment channel

11. How shall it look?
Alice Bob
payment channel
1 BTC 1 BTC
1. Initially they put some money into the channel,
2. and they decide how much money goes to each
party.

12. For example, initially the “state” of the
channel is as follows:
payment channel
1 BTC1 BTC
Important: this is just a “virtual” payment (it is not
“formalized” on the blockchain).

13. Channel adjustment
Suppose Alice wants to pay to Bob 0.01 BTC.
Then they can “adjust” the channel as follows:
payment channel
Alice Bob
1 BTC1 BTC 1.01 BTC0.99 BTC

14. In general
Given a “state” (with non-negative x and y such that 𝐱 + 𝐲 = 𝟐):
payment channel
y BTCx BTC
Alice Bob
Alice can pay to Bob any amount 𝐱′ ≤ 𝐱 by adjusting the
channel to:
payment channel
y+x’ BTCx-x’ BTC
Alice Bob

15. Symmetrically:
payment channel
y BTCx BTC
Alice Bob
Bob can pay to Alice any amount 𝐲′
≤ 𝐲 by adjusting the
channel to:
payment channel
y-y’ BTCx+y’ BTC
Alice Bob

16. Closing the channel
At the end Alice and Bob can close the channel, and get
the “real money”.
General picture: founding the
channel
adjustments
closing the channel
only these phases
require
blockchain
operations
this can be done
“offline” (hence:
for free and very
efficiently)

17. How to construct such a channel?
Let’s start with “unidirectional” channels, where only Alice
can pay to Bob.
The initial state is as follows:
Alice Bob
payment channel
1 BTC
0 BTC1 BTC

18. Tool: mulisignature transactions
The Bitcoin scripts permit to create
k-out-of-n mulisignature transactions.
These are transactions that can be claimed only by providing
signatures from k users (from some set of n users).
Example: a 2-out-of-2 multisignature transaction
T2 =
can be spent by any
transaction that has
signatures of Alice and Bob
signature of CarolT1
1
BTC
some unspent transaction of Carol
Then T2 can be redeemed by
can be spent by Dave
signature of Alice
T2
1
BTC
signature of Bob

19. Convention
T2 =
can be spent by any
transaction that has
signatures of Alice and Bob
signature of CarolT1
1
BTC
we will write
Carol sends 1 BTC from T1 to Alice&Bob signature of Carol𝐓𝟐 =
Instead of

20. Founding a channel
Alice sends 1 BTC from T to Alice&Bob signature of Alice𝐓𝟎 =
Alice creates a founding transaction 𝐓𝟎 as follows:
some unspent transaction of Alice
Can Alice post 𝐓𝟎 on the blockchain or show it to Bob?
No! Then her money from T could be locked forever.

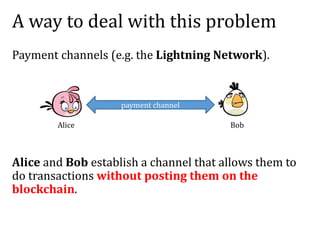
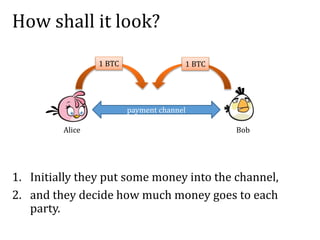
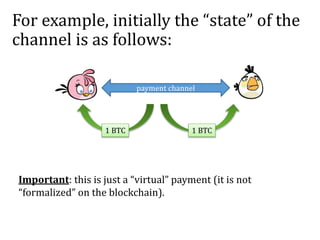
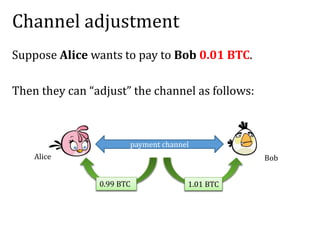
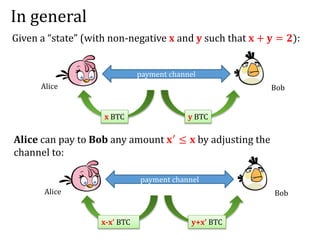
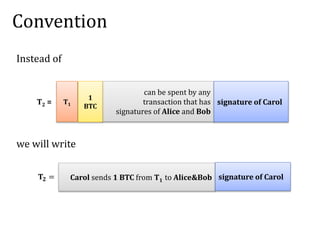
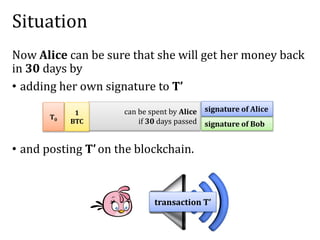
21. Solution: Alice asks Bob to sign a “refund”
transaction T’ with a timelock.
Please sign the following:
[T’] =
can be spent by Alice
if 30 days passed
T0
1
BTC
ok, here is my signature
Good news: technically this can be done without showing T’ to Bob.
Bad news: this solution has problems with transaction malleability
(but let’s ignore them here).
signature of Bob

22. Situation
Now Alice can be sure that she will get her money back
in 30 days by
• adding her own signature to T’
• and posting T’on the blockchain.
transaction T’
can be spent by Alice
if 30 days passed signature of Bob
T0
1
BTC
signature of Alice

23. First blockchain transaction
Since Alice is sure that she will get her money back, she
can now post T0 on the blockchain.
transaction T0

24. How to make a micropayment
Alice sends 0.99 BTC from T0 to Alice,
Alice sends 0.01 BTC from T0 to Bob
if 29 days have passed
signature of Alice𝐓𝟏 =
In order to send 0.01 BTC to Bob, Alice sends to Bob a
transaction 𝐓𝟏 constructed as:
𝐓𝟏
How can Bob get the real money from 𝐓𝟏?
He can just add his own signature and post 𝐓𝟏 on the blockchain.
Important: he has to do it before day 30 (as otherwise Alice
can steal all the money)
signature of Bob

25. And so on…
Alice sends 0.98 BTC from T0 to Alice,
Alice sends 0.02 BTC from T0 to Bob
if 29 days have passed
signature of Alice
𝐓𝟐 =
In order to further send 0.01 BTC to Bob, Alice sends to Bob a
transaction 𝐓𝟐 constructed as:
Alice Bob
𝐓𝟏

26. In general to send y BTC:
if the last transaction sent by Alice to Bob was:
then Alice can sends to Bob the following transaction:
𝐓𝐢+𝟏 =
Alice sends x BTC from T0 to Alice,
Alice sends 1-x BTC from T0 to Bob
if 29 days have passed
signature of Alice
𝐓𝐢 =
Alice sends x-y BTC from T0 to Alice,
Alice sends 1-(x-y) BTC from T0 to Bob
if 29 days have passed
signature of Alice

27. How to close the channel?
If Bob wants to close the channel then he simply adds
his signature and posts the last 𝐓𝐢 on the blockchain (at
day 29).
Observe: the 𝐓𝐢’s only get better and better for him.
Therefore he will always post the last 𝐓𝐢.
To close the channel Alice has to wait (or ask Bob).

28. Suppose Bob wants to send money
back to Alice.
How to “invert the channel”?
The situation with the unidirectional channels:
Bob’s
payout
time
1 BTC

29. We want:
Bob’s
payout
time
1 BTC
Observe: in these periods it’s Alice
who is “gaining money with time”

30. Let’s concentrate on single inversion:
Suppose the state of the channel is
(1-y BTC to Alice, y BTC to Bob)
Bob’s
payout
1 BTC
y BTC

31. Solution
Invert the situation: let now Bob send “signed
transactions” to Alice.
To send y BTC from Bob to Alice:
Alice sends 1-(y-y’) BTC from T0 to Alice,
Alice sends y-y’ BTC from T0 to Bob
if 28 days have passed signature of Bob
𝐓𝐢 =
Alice Bob
𝐓𝐢
why 28?

32. Why the timelock is “28 days” now?
Remember: Bob is now “loosing money”.
At day 29 he could post the transaction that gives
him y BTC…
Bob’s
payout
1 BTC
y BTC
Alice needs to be able to “react” earlier (in day 28).

33. Payment networks
Problem: every pair of parties requires a separate
channel…
Can we do better?
Yes! We can let the parties “route” the payments.
channel channel channel
Alice Bob Carol Dave
Alice pays to Dave using Bob and Carol as intermediaries
(possibly at a fee).

34. What if Alice and Dave do not trust the
intermediaries?
There is a solution that uses
hash-locked transactions
H – hash function
Let Y := H(X)
A Y-hash-locked transaction from A to B can be
redeemed only by publishing X:
T2 =
can be spent using B’s
signature and X such that
Y = H(X)
A’s
signature
T1
1
BTC

35. How can it be used?
Sketch of the solution:
channel channel channel
Alice Bob Carol Dave
generates random X
and computes Y = H(X)
Y
I pay you a 0.01 if
you show me X such
that Y = H(X)
I pay you a 0.01 if
you show me X such
that Y = H(X)
I pay you a 0.01 if
you show me X such
that Y = H(X)
XXX

36. Improvements
Assuming some improvements in Bitcoin, the Lightning
network achieves the following:
• channels can be open “forever” (no need to have
specified timelocks)
• but can be reasonably quickly closed at a request of
any party.

37. ©2016 by Stefan Dziembowski. Permission to make digital or hard copies of part or
all of this material is currently granted without fee provided that copies are made
only for personal or classroom use, are not distributed for profit or commercial
advantage, and that new copies bear this notice and the full citation.