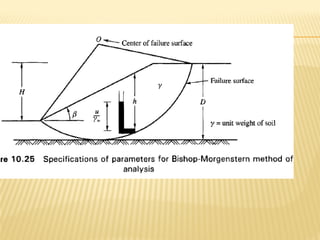
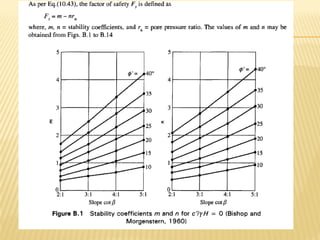
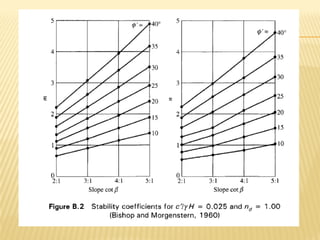
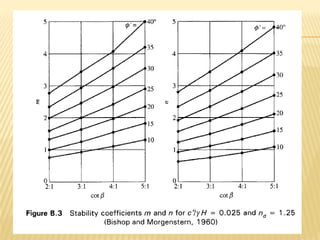
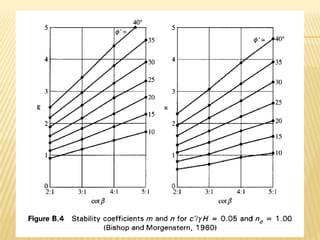
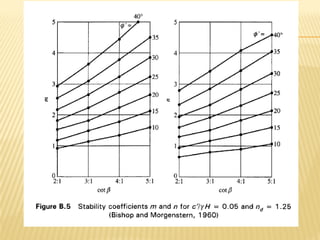
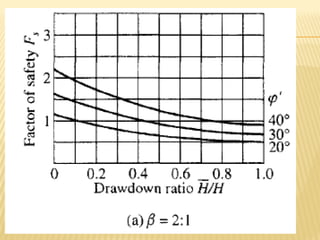
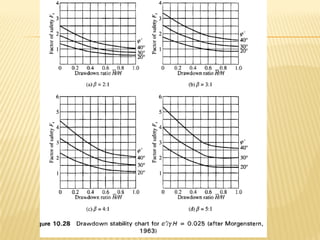
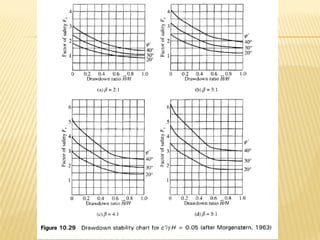
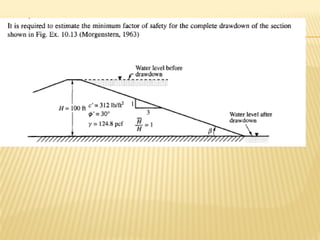
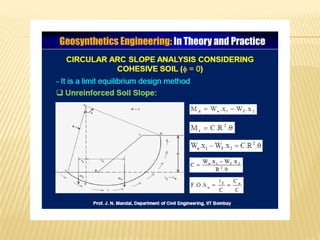
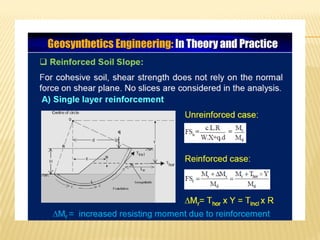
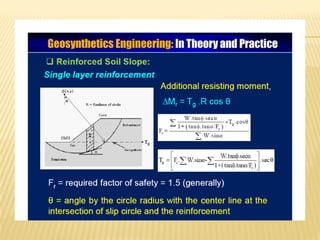
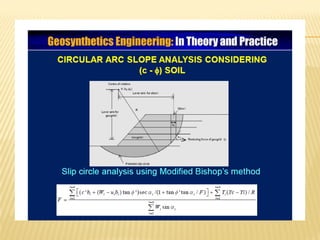
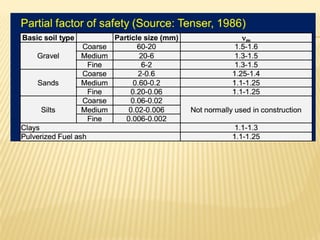
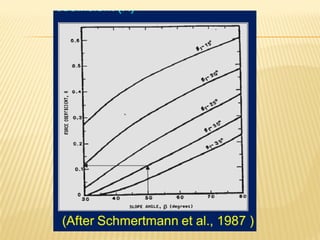
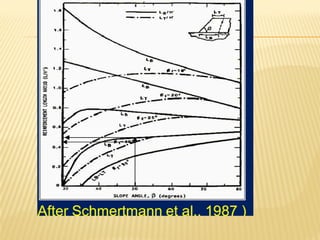
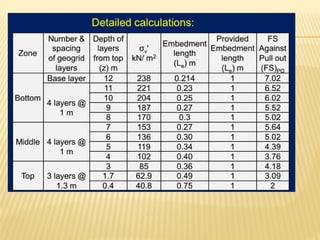
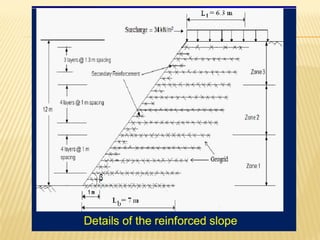
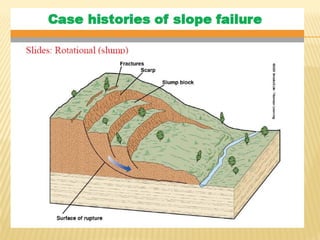
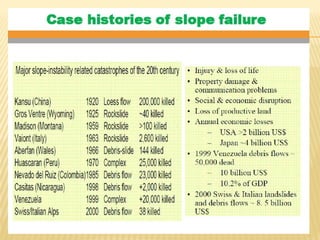
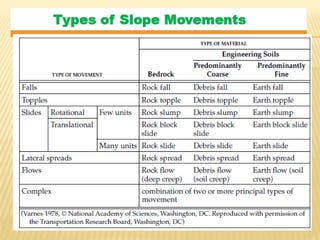
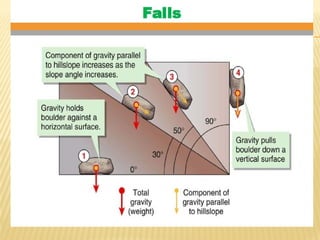
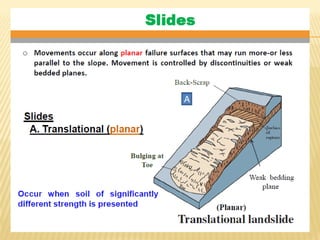
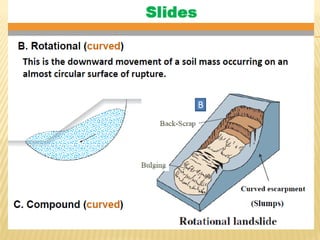
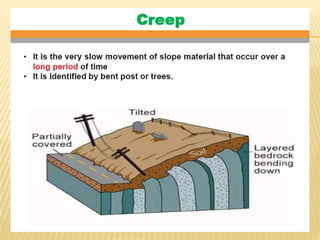
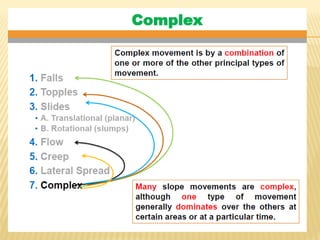
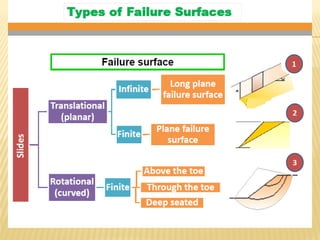
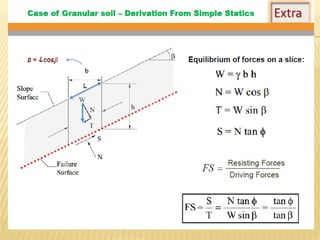
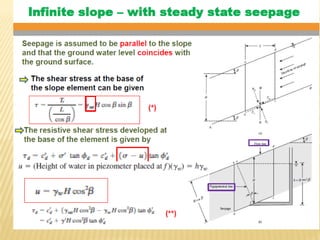
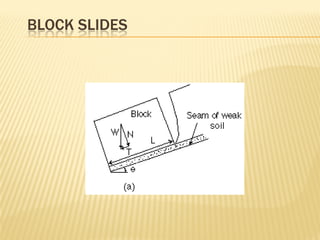
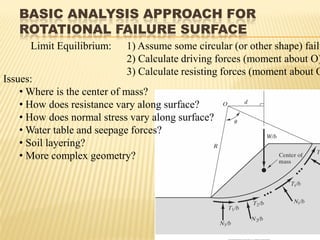
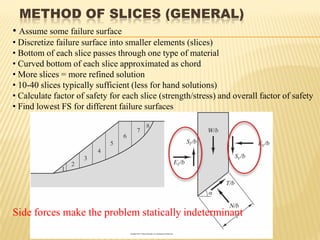
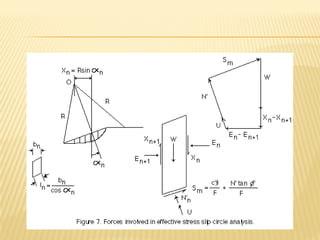
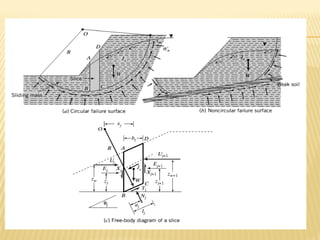
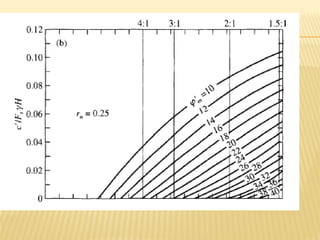
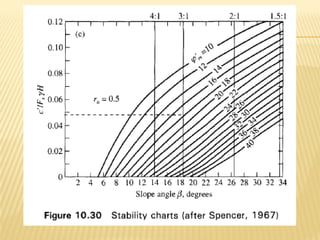
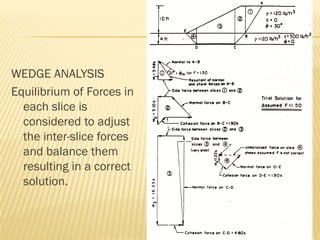
The document discusses methods for analyzing slopes, earth-retaining structures, and underground structures, focusing on finite slopes and failure surfaces. It details various approaches, including the method of slices, which involves discretizing failure surfaces to calculate factors of safety for slope stability. Several specific methods are highlighted, such as the Ordinary Method of Slices, Bishop's Simplified Method, and Spencer's Method, each tailored for different conditions and types of soil.

1. ANALYSIS OF SLOPES, EARTH RETAINING
STRUCTURES AND UNDERGROUND STRUCTURES
CENG 6208
ARGAW.A (PHD)

36. 36

37. 37

38. 38

39. 39

52. FINITE SLOPES: PLANE FAILURE
SURFACE
 Translational Block Slides along single
plane of weakness or geological interface
 F = c’L + (W cosθ − uL) tanφ’ / W sinθ + Fw

53. BLOCK SLIDES

54. Limit Equilibrium: 1) Assume some circular (or other shape) failu
2) Calculate driving forces (moment about O)
3) Calculate resisting forces (moment about O
BASIC ANALYSIS APPROACH FOR
ROTATIONAL FAILURE SURFACE
Issues:
• Where is the center of mass?
• How does resistance vary along surface?
• How does normal stress vary along surface?
• Water table and seepage forces?
• Soil layering?
• More complex geometry?

55. METHOD OF SLICES (GENERAL)
• Assume some failure surface
• Discretize failure surface into smaller elements (slices)
• Bottom of each slice passes through one type of material
• Curved bottom of each slice approximated as chord
• More slices = more refined solution
• 10-40 slices typically sufficient (less for hand solutions)
• Calculate factor of safety for each slice (strength/stress) and overall factor of safety
• Find lowest FS for different failure surfaces
Side forces make the problem statically indeterminant

56. SLOPE ANALYSIS METHODS:
ROTATIONAL FAILURE SURFACE
“OMS”
“Modified Bishop’s”

57. FINITE SLOPES: CIRCULAR FAILURE
SURFACE
 Rotational Slides - Method of Slices
 Applies to slopes containing cohesive soils
 Ordinary Method of Slices (Fellenius’ Method)
 Bishop’s Simplified Method
 Spenser’s Method

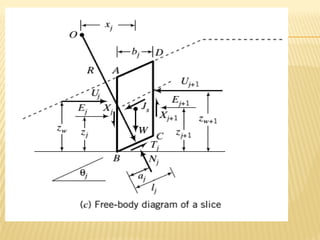
61. ORDINARY METHOD OF SLICES
 Assumes that resultant of side forces on each
slice are collinear and act parallel to failure
surface and therefore cancel each other
 F = Σ[cn ln + (Wn cosαn - un ln) tanφn] / ΣWn sinαn
 Undrained analysis: F = Σ[cn ln] / ΣWn sinαn

62. SIDE FORCES IN ORDINARY METHOD OF
SLICES

63. BISHOP’S SIMPLIFIED METHOD
 Assumes that resultant of side forces on each slice
act in horizontal direction and therefore vertical
side force components cancel each other
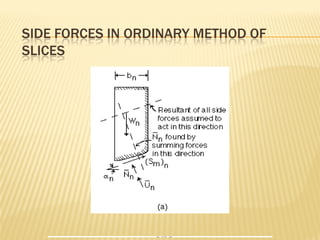
 F = Σ[cn bn + (Wn - un bn) tanφn](1/mα) / ΣWn sinαn
 mα = cosαn + (sinαn tanαn)/F
 Undrained analysis: F = Σ[cn ln] / ΣWn sinαn

64. CHART FOR Mα

65. SIDE FORCES IN
BISHOP’S METHOD

66. SPENCER’S METHOD
 Assumes that the point of application of
resultant of side forces on each slice is at mid-
height of each slice but no assumption is made
regarding inclination of resultants; inclination is
determined as part of the solution
 This method is more exact than Bishop’s

70. FINITE SLOPES: NONCIRCULAR FAILURE
SURFACE
 Wedge Method
 Janbu’s Simplified Method
 Morgenstern-Bishop Method

71. WEDGE METHOD
 Failure surface consists of two or more planes
and applicable to slope containing several
planes of interfaces and weak layers
 Force equilibrium is satisfied
 Assumes that resultant of side forces on each
slice either acts horizontally or at varying
angles from horizontal (typically up to 15o)

72. WEDGE METHOD
Layer B
Layer A
4
3
2
1
φm
θ

73. WEDGE ANALYSIS
Equilibrium of Forces in
each slice is
considered to adjust
the inter-slice forces
and balance them
resulting in a correct
solution.

74. JANBU’S SIMPLIFIED METHOD
 A method of slices applicable to circular and
noncircular failure surfaces
 F = fo Σ{[cn bn + (Wn - un bn) tanφn](1/ cosαnmα)}
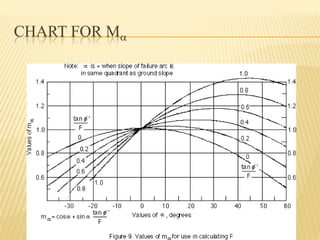
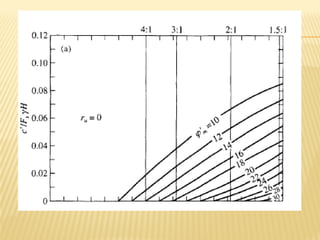
/ ΣWn tanαn
 fo is a correction factor that varies with depth to
length ratio of sliding mass and type of soil
(φ = 0, c, φ or c = 0)

75. Fa cto r, f
o
R a tio, d /L
φ = 0
c, φ so il
c = 0
L
d

76. MORGENSTERN-BISHOP METHOD
 No assumption is made regarding inclination or
point of application of resultants and these are
determined as part of the solution
 Requires computers for solving the basic
equation
 Exact but not practical

83. MORGENSTERN RAPID DRAWN CONDITION

88. GEOSYENTHITICS