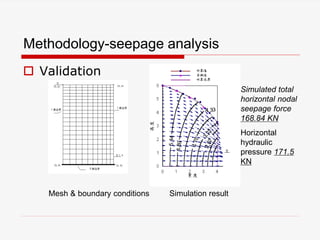
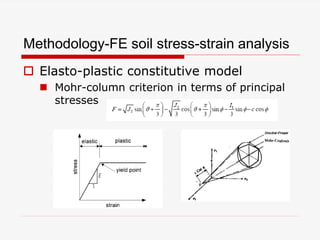
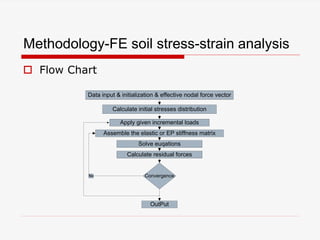
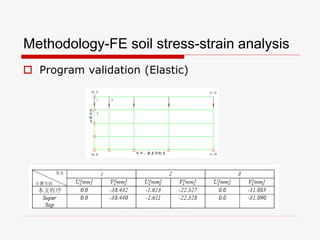
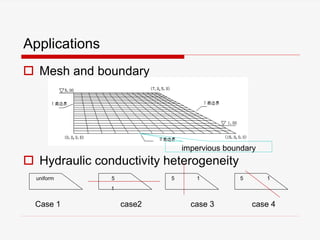
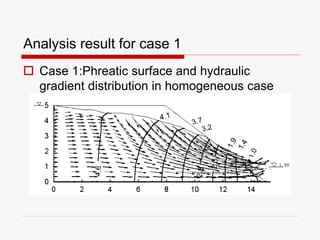
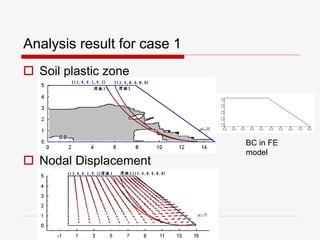
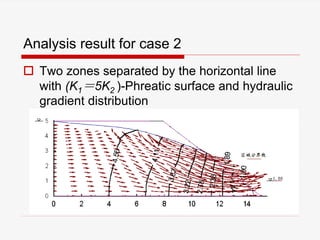
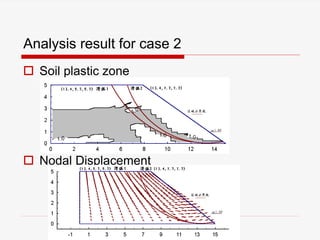
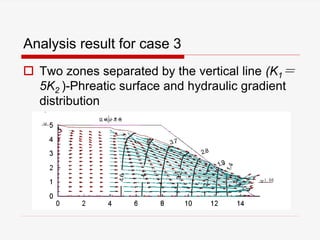
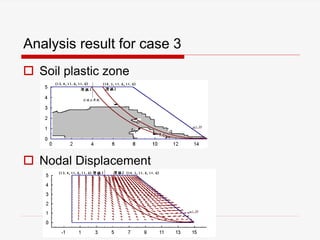
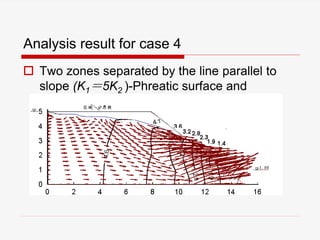
The document presents a finite element analysis (FEA) of groundwater seepage and soil slope stability, detailing methodologies for modeling seepage effects on soil stability. It discusses the implementation of a FEA program for analyzing pore pressure distribution, phreatic surface, and elasto-plastic soil stress-strain responses under varying conditions. The results indicate that non-homogeneous hydraulic conductivity significantly impacts soil slope stability, with findings closely aligning with traditional limit equilibrium methods.

1. FE Numerical Coding and Analysis on
Seepage & Slope Stability
Presented by: Wang Xuejun
Email: wangxuejun@gmail.com
LinkedIn: www.linkedin.com/in/wangxuejun
Master thesis work in Tianjin Univ. (1996- 1999)

2. Outline
 Introduction
 Methodology
 FE ground water seepage analysis
 FE soil slope stability analysis
 Applications
 Concluding remarks

3. Introduction
 Seepage reduces the stability of soil slope
 Seepage makes it easier for soil particles to slide
over each other during failure
 Pore water pressures reduce the inherent strength
and stability of a soil mass
 Analysis methods
 The classical slope stability analysis based on
limit equilibrium (generally using method of slices)
 Numeric solutions mostly based on the finite
elements method

4. Introduction
 Total stress method (left) .vs. effective
stress method (right)
surrounding water pressure
soil saturated density
seepage force (pore pressure)
soil buoyancy density

5. Introduction
A FEM based program is developed to analyze
slope stability under seepage
 Stead state flow modeling
 Phreatic surface & pore pressure distribution
 Seepage force
 Elasto-plastic soil stress-strain modeling
 Plastic zone to predict the slope failure
 Result comparison between the FE method and
Classic method

6. Methodology-seepage analysis
 Use Darcy Rule to solve pore pressure
distribution & phreatic surface
 Steady flow
 Saturated flow
0)()( 









y
h
k
yx
h
k
x
yx
impervious boundary
phreatic
surface

7. Methodology-seepage analysis
 FE program implementation-flow chart
Start
Data input, Initialization, Check
Element stiffness; Assemble to give the global
stiffness matrix & ‘load’ vector
Gauss elimination solver
Check pore pressure for each nodes
Mark nodes & modified node water
head information
Satisfied
Calculate phreatic surface
Seepage gradient
Seepage force on nodes
Iteration
OutPut
end
No

8. Methodology-seepage analysis
 FE program implementation
 Numerical integration
 Nodal seepage force
 Hydraulic gradient
 Nodal seepage force as the body force















yh
xh
i
i
i
y
x
    ( ) ( ) ( ) ( ) ( )
1
Nge T T
ig ig ig ig igi
ig
i dxdy W N i g JF N   

  

9. Methodology-seepage analysis
 Phreatic surface solved using iteration method
 Abandon& mark all elements above the upper-
stream water level
 Solve & check nodal water head by
h≥Z+ERROR
 Mark those nodes violate & abandon by
modifying the GM
 Iteration till convergence
 Phreatic surface obtained by interpolation between
those transition elements








ii
ji
ij
ZF
ijnjK
ijnjK
);,1(0
);,1(0

10. Methodology-seepage analysis
 Validation
Mesh & boundary conditions Simulation result
Simulated total
horizontal nodal
seepage force
168.84 KN
Horizontal
hydraulic
pressure 171.5
KN

11. Methodology-FE soil stress-strain analysis
 Elasto-plastic constitutive model
 Mohr-column criterion in terms of principal
stresses

12. Methodology-FE soil stress-strain analysis
 Elastic calculation using Hook’s Law
 Plastic calculation-associated flow rule
 Strain decomposition
 Incremental stress calculation
 Hardening law in differential form
 Nonlinear solver
 Combination of the initial & tangential stiffness method
 
 '
p
p
d
H
d





13. Methodology-FE soil stress-strain analysis
 Flow Chart
Data input & initialization & effective nodal force vector
Calculate initial stresses distribution
Apply given incremental loads
Assemble the elastic or EP stiffness matrix
Solve euqations
Calculate residual forces
ConvergenceNo
OutPut

14. Methodology-FE soil stress-strain analysis
 Program validation (Elastic)

15. Applications -slope stability under seepage
analysis
 Consider hydraulic conductivity
heterogeneity in soil slope by dividing
into two different zones
 Use soil plastic zone to predict potential
sliding surface
 Used other methods based on the FE
simulated stress distributions
 Use limited equilibrium methods

16. Applications
 Mesh and boundary
 Hydraulic conductivity heterogeneity
impervious boundary
Case 1 case2 case 3 case 4
uniform 5 5 1 5 1
1

17. Analysis result for case 1
 Case 1:Phreatic surface and hydraulic
gradient distribution in homogeneous case

18. Analysis result for case 1
 Soil plastic zone
 Nodal Displacement
BC in FE
model

19. Analysis result for case 2
 Two zones separated by the horizontal line
with (K1＝5K2 )-Phreatic surface and hydraulic
gradient distribution

20. Analysis result for case 2
 Soil plastic zone
 Nodal Displacement

21. Analysis result for case 3
 Two zones separated by the vertical line (K1＝
5K2 )-Phreatic surface and hydraulic gradient
distribution

22. Analysis result for case 3
 Soil plastic zone
 Nodal Displacement

23. Analysis result for case 4
 Two zones separated by the line parallel to
slope (K1＝5K2 )-Phreatic surface and
hydraulic gradient distribution

24. Analysis result for case 4
 Soil plastic zone
 Nodal Displacement

25. Other methods based on FE results
 Factor of safety method (for a given
potential sliding surface)
 Force equilibrium method



F

i i
S
i
l
K
l




( )
n
i i i i
i
F n
i i
i
f c l
K
l


 




Potential sliding
surface
Element cut by
potential sliding
surface

26. Results
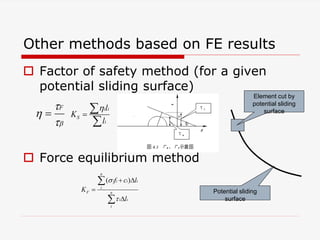
 Comparison of different methods
FE Limited Equilibrium
KS KF KB
Case 1 Surface 1 [13.4 , 9.2 , 9.2 ] 1.190 1.095 1.069
surface 2 [13.4 , 8.0 , 8.0 ] 1.216 1.088 1.155
Case 2 Surface 1 [13.4 , 9.2 , 9.2 ] 1.125 1.070 1.031
surface 2 [13.4 , 8.0 , 8.0 ] 1.172 1.075 1.057
Case 3 Surface 1 [13.4 , 9.2 , 9.2 ] 1.078 1.119 1.067
surface 2 [13.4 , 8.0 , 8.0 ] 1.215 1.100 1.067
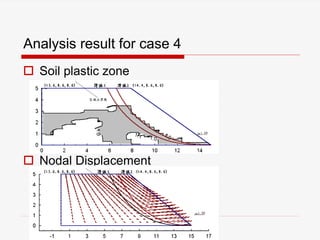
Case 4 Surface 1 [13.4 , 9.2 , 9.2 ] 1.075 1.030 0.994
surface 2 [13.4 , 8.0 , 8.0 ] 1.077 1.018 1.067

27. Concluding remarks
 An alternative method to predict the slope
failure surface induced by the seepage.
 Result shows good agreement with that by
limited equilibrium method (simplified Bishop
method) using FE predicted ground water
table.
 Non-homogenous hydraulic conductivity has
great influence on the soil slope stability.

28. Thank you