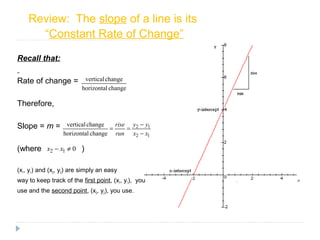
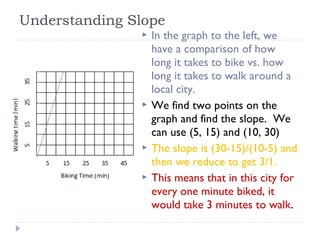
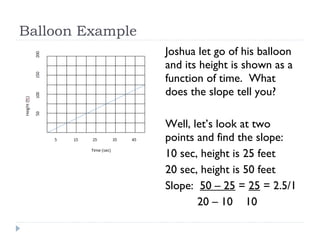
Rate of change and slope allow us to understand the relationship between variables. Rate of change is the change in the dependent variable over the change in the independent variable. Slope is the constant rate of change between two points and is calculated as the rise over the run. Slope can tell us how one quantity changes in relation to another, such as pages read per minute, cost per text, or speed of descent.

1. Rate of Change & Slope

2. Rate of Change
Rate of change allows us to look at the relationship between different quantities. Rate
of change is expressed as a ratio of the dependent variable (y) and the independent
variable (x).
Rate of change =
You can find the rate of change over an interval by finding the difference. You can
compare the rate over change for different intervals to determine where the least and
greatest rate of change occurs.
change in dependent variable
change in independent variable

3. Review: The slope of a line is its
“Constant Rate of Change”
Recall that:
Rate of change =
Therefore,
Slope = m =
(where )
(x1, y1) and (x2, y2) are simply an easy
way to keep track of the first point, (x1, y1), you
use and the second point, (x2, y2), you use.
012 ≠− xx
changehorizontal
changevertical
12
12
changehorizontal
changevertical
xx
yy
run
rise
−
−
==

4. Let’s look at a table
Number of Pages Read 5 15 25 35 45
Amount of Time in Minutes 8 12 16 20 24
Joanna recorded the number of minutes she read and how
many pages she read during that time. What does the slope
tell us about the number of pages she reads?
We will use the first two values in the table to find the slope.
Slope = 12 – 8 = 4/5 = 0.8/1
15 – 5
So that means she reads 4 pages in five minutes or 0.8 pages
in one minute.

5. Let’s try another one!
Number of texts 100 200 300 400 500
Jarrod’s Bill $20 $30 $40 $50 $60
Mike’s Bill $17 $29 $41 $53 $65
What can be determined about which person pays the most
money per text? How much more?
We are going to find the slope for Jarrod and Mike’s bill,
and then compare those slopes to answer the question.

6. Let’s Compare Slopes
 Jarrod’s Bill
30.00 – 20.00
200 – 100
10 dollars/100 texts
$0.10/text
 Mike’s Bill
29.00 – 17.00
200 – 100
12 dollars/100 texts
$0.12/text
Even though Mike paid less money for the smaller number
of texts, he is still paying $0.02 more per text!

7. Understanding Slope
 In the graph to the left, we
have a comparison of how
long it takes to bike vs. how
long it takes to walk around a
local city.
 We find two points on the
graph and find the slope. We
can use (5, 15) and (10, 30)
 The slope is (30-15)/(10-5) and
then we reduce to get 3/1.
 This means that in this city for
every one minute biked, it
would take 3 minutes to walk.

8. What do we do with slope?
 We can use the slope to understand the relationship between the variables.
 Example: When Marvin works 8 hours, he earns $78 He
earns $68.25 when he works for 7 hours. What is the rate
of change?
 So, we use our slope formula:
78 – 68.25 = 9.75 (dollars)
8 – 7 1 (hour)
If we think about the units of the slope, we realize that
this is saying he makes $9.75 for working one hour. So
Marvin makes $9.75 an hour.

9. In terms of an equation
 A local cab company charges by the mile to drive
passengers from one location to another. The equation
can be written as C(m) = 0.85m + $3.00 where m stands
for the number of miles and C(m) stands for the total
cost. What can we conclude about the equation
according to its slope?
 If we think about this equation, we have two numbers in play.
The $3.00 is just a flat rate. You would need to pay that $3.00
just for using the cab.
 We notice that the $0.85/1 is multiplied by the number of
miles, so that is our slope and tells us that each mile travelled
will cost $0.85.

10. Balloon Example
Joshua let go of his balloon
and its height is shown as a
function of time. What
does the slope tell you?
Well, let’s look at two
points and find the slope:
10 sec, height is 25 feet
20 sec, height is 50 feet
Slope: 50 – 25 = 25 = 2.5/1
20 – 10 10

11. So what does this mean?
It means that it takes the balloon
10 seconds to travel 25 feet, or
one second to take 2.5 feet. So,
we can say that the balloon
travels 2.5 feet/second.

12. Bird Example
A bird descends from the sky
according to the graph at the
left. What does the slope
tell us?
Well, let’s look at two points
and find the slope:
0 seconds, 200 feet
15 seconds, 125 feet
Slope: 125 - 200 = -75 = -5/1
15 – 0 15

13. So what does this mean?
It means that over a time of 15
seconds, the bird descends 75
feet. Or, after one second, the
bird descends 5 feet. So the bird
travels down 5 feet/second.