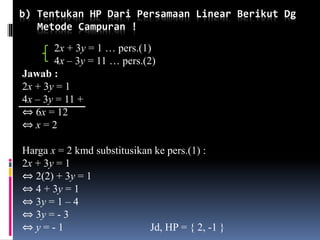
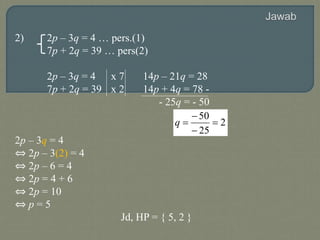
Dokumen ini membahas sistem persamaan linear dua variabel (SPLDV) dan menyajikan metode penyelesaian yang meliputi eliminasi, substitusi, campuran, dan determinan. Setiap metode diilustrasikan melalui contoh yang menunjukkan langkah-langkah penyelesaian dan himpunan penyelesaian. SPLDV merupakan alat penting dalam matematika yang melibatkan dua variabel yang tidak diketahui, sehingga dibutuhkan pemahaman berbagai metode untuk menyelesaikannya.

1. SISTEM PERSAMAAN LINEAR
DUA VARIABEL (SPLDV)
SMK TUNAS MEDIA
OLEH
ABDUL MAJID, M.Pd

2. Sistem persamaan linear dua variabel adlh sistem
persamaan yg mengandung dua variabel yg tdk diketahui.
Bentuk Umumnya :
ax + by = c … persamaan (1)
px + qy = r … persamaan (2)
Dg a, b, c, p, q & r ϵ R
a, p = koefisien dari x
b, q = koefisien dari y
Ada 4 metode penyelesaian SPLDV tsb, yaitu :
1) Metode Eliminasi
2) Metode Substitusi
3) Metode Campuran
4) Metode Determinan

3. 1. Metode Eliminasi
Metode ini digunakan dg cara mengeliminasi
(menghilangkan) salah satu variabelnya, shg
diperoleh sebuah persamaan dg satu variabel.
Contoh :
Tentukan Himpunan Penyelesaian (HP) dari
persamaan linear berikut dg metode eliminasi !
2x + 3y = 1 … pers.(1)
3x + y = 5 … pers.(2)
Jawab :
Mengeliminasi x
2x + 3y = 1 x3 6x + 9y = 3
3x + y = 5 x2 6x + 2y = 10 –
7y = - 7
y = -1

4. Mengeliminasi y
2x + 3y = 1 x1 2x + 3y = 1
3x + y = 5 x3 9x + 3y = 15 –
- 7x = - 14
x = 2
Jd, HP = { 2, -1 }
Catatan :
“ Jika kita mengeliminasi (menghilangkan) variabel x
maka yg akan kita dapatkan nantinya adlh nilai dari variabel y
dan sebaliknya, jika kita mengeliminasi variabel y maka yg
akan kita dapatkan nantinya adlh nilai dari variabel x “

5. Tentukan HP dari SPL berikut ini dg menggunakan metode eliminasi !
1) 2x – y = 2
3x – 2y = 1 Jawab
2) 3x + 5y = 4
3x – y = 10 Jawab
3) 5x + y = 5
17x + y = - 5 Jawab
4) 2p – 3q = 4
7p + 2q = 39 Jawab
Ke slide Metode Substitusi

6. Jawab
1) * Mengeliminasi variabel y
2x – y = 2 x 2 4x – 2y = 4
3x – 2y = 1 x 1 3x – 2y = 1 -
x = 3
* Mengeliminasi variabel x
2x – y = 2 x 3 6x – 3y = 6
3x – 2y = 1 x 2 6x – 4y = 2 -
y = 4
Jd, HP = { 3, 4}
Kembali ke slide soal

7. Jawab
2) * Mengeliminasi variabel x
3x + 5y = 4
3x – y = 10 -
6y = - 6
y = - 1
* Mengeliminasi variabel y
3x + 5y = 4 x 1 3x + 5y = 4
3x – y = 10 x 5 15x – 5y = 50 +
18x = 54
x = 3
Jd, HP = { 3, - 1}
Kembali ke slide soal

8. Jawab
3) * Mengeliminasi variabel y
5x + y = 5
17x + y = - 5 -
- 12x = 10
* Mengeliminasi variabel x
5x + y = 5 x 17 85x + 17y = 85
17x + y = - 5 x 5 85x + 5y = - 25 -
12y = 110
Kembali ke slide soal
6
5
12
10




x
6
1
9
12
2
9
12
110



y
}
{
6
1
9
,
6
5


HP

9. Jawab
4) * Mengeliminasi variabel p
2p – 3q = 4 x 7 14p – 21q = 28
7p + 2q = 39 x 2 14p + 4q = 78 -
- 25q = - 50
* Mengeliminasi variabel q
2p – 3q = 4 x 2 4p – 6q = 8
7p + 2q = 39 x - 3 - 21p - 6q = - 117 -
25p = 125
Jd, HP = { 5, 2} Kembali ke slide soal
2
25
50




q
5
25
125


p

10. 2. Metode Substitusi
Pada metode ini, salah satu variabel dari salah satu
persamaan disubstitusikan shg diperoleh sebuah persamaan
dg satu variabel saja
Contoh :
a) Tentukan HP dari persamaan linear berikut dg metode
substitusi !
3x + 4y = 11 … pers.(1)
x + 7y = 15 … pers.(2)
Jawab :
Dari pers.(2) didapat : x = 15 – 7y … pers.(3)
Kmd substitusikan pers.(3) ke pers.(1) :
3x + 4y = 11 Harga y = 2 kmd
⇔ 3(15 – 7y) + 4y = 11 substitusikan ke
pers(3) :
⇔ 45 – 21y + 4y = 11 x = 15 – 7y
⇔ - 21y + 4y = 11 – 45 x = 15 – 7(2)
⇔ - 17y = - 34 ⇔ x = 15 – 14
2
17
34




y

11. 2x + 3y = 1 … pers.(1)
3x + y = 5 … pers.(2)
Jawab :
Dari pers.(2) didapat : y = 5 – 3x … pers.(3). Harga x = 2 kmd
Kmd substitusikan pers.(3) ke pers.(1) : disubstitusikan ke pers.(3) :
2x + 3y = 1 y = 5 – 3x
2x + 3(5 – 3x) = 1 y = 5 – 3(2)
2x + 15 – 9x = 1 y = 5 – 6
2x – 9x = 1 – 15 y = - 1
- 7x = - 14
x = 2 Jd, HP = { 2, - 1}

12. 1) 2x – y = 2
3x – 2y = 1 Jawab
2) 3x + 5y = 4
3x – y = 10 Jawab
3) 5x + y = 5
17x + y = - 5 Jawab
4) 2p – 3q = 4
7p + 2q = 39 Jawab

13. Jawab
1) 2x – y = 2 … pers.(1)
3x – 2y = 1 … pers.(2)
Dari pers.(1) didapat : Harga x = 3 kmd disubstitusikan
- y = 2 – 2x ⇔ y = - 2 + 2x … pers.(3) ke pers.(1) :
Kmd substitusikan pers.(3) ke pers.(2) : 2x – y = 2
⇔ 3x – 2y = 1 ⇔ 2(3) – y = 2
⇔ 3x – 2(-2 + 2x) = 1 ⇔ 6 – y = 2
⇔ 3x + 4 – 4x = 1 ⇔ - y = 2 – 6
⇔ 3x – 4x = 1 – 4 ⇔ - y = - 4
⇔ - x = - 3 ⇔ y = 4
⇔ x = 3
Jd, HP = { 3, 4}

14. Jawab
2) 3x + 5y = 4 … pers.(1)
3x – y = 10 … pers.(2)
Dari pers.(2) didapat : Harga x = 3 kmd disubstitusikan
- y = 10 – 3x ⇔ y = - 10 + 3x … pers.(3) ke pers.(2) :
Kmd substitusikan pers.(3) ke pers.(1) : 3x – y = 10
⇔ 3x + 5y = 4 ⇔ 3(3) – y = 10
⇔ 3x + 5(-10 + 3x) = 4 ⇔ 9 – y = 10
⇔ 3x – 50 + 15x = 4 ⇔ - y = 10 – 9
⇔ 3x + 15x = 4 + 50 ⇔ - y = 1
⇔ 18x = 54 ⇔ y = - 1
⇔ x = 3
Jd, HP = { 3, - 1 }

15. Jawab
3) 5x + y = 5 … pers.(1)
17x + y = - 5 … pers.(2)
Dari pers.(1) didapat : Harga
y = 5 – 5x … pers.(3) kmd disubstitusikan ke pers.(1) :
Kmd substitusikan pers.(3) ke pers.(2) : 5x + y = 5
17x + y = - 5
⇔ 17x + 5 – 5x = - 5
⇔ 17x – 5x = - 5 – 5 ( x 6 )
⇔ 12x = - 10 ⇔ - 25 + 6y = 30
⇔ 6y = 30 + 25
⇔ 6y = 55
6
5
12
10




 x
6
5


x
5
6
5
5 )
( 


 y
5
6
25
)
( 


 y
6
1
9
6
55


 y
}
{
6
1
9
,
6
5


HP

16. Jawab
4) 2p – 3q = 4 … pers.(1)
7p + 2q = 39 … pers.(2)
Dari pers.(1) didapat : Harga q = 2 kmd disubstitusikan
2p – 3q = 4 ⇔ 2p = 4 + 3q ke pers.(1) :
2p – 3q = 4
Kmd substitusikan pers.(3) ke pers.(2) : ⇔ 2p – 3(2) = 4
⇔ 7p + 2q = 39 ⇔ 2p – 6 = 4
⇔ 2p = 4 + 6
⇔ 2p = 10
⇔ p = 5
( x 2)
⇔ 28 + 21q + 4q = 78 Jd, HP = { 5, 2 }
⇔ 21q + 4q = 78 – 28
⇔ 25q = 50 ⇔ q = 2
)
3
.(
...
2
3
4
pers
q
p



39
2
2
3
4
7 )
( 


 q
q
39
2
2
21
28
)
( 


 q
q

17. 3. Metode Campuran
Pada metode ini, merupakan gabungan dari cara
eliminasi dan substitusi.
Contoh :
a) Tentukan HP dari persamaan linear berikut dg metode
campuran !
3x + 4y = 11 … pers.(1)
x + 7y = 15 … pers.(2)
Jawab :
3x + 4y = 11 x 1 3x + 4y = 11
x + 7y = 15 x 3 3x + 21y = 45 -
- 17y = - 34
⇔ y = 2
Harga y = 2 kmd substitusikan ke pers(2) :
x + 7y = 15
⇔ x + 7(2) = 15
⇔ x + 14 = 15
⇔ x = 15 – 14 ⇔ x = 1 Jd, HP = { 1,

18. b) Tentukan HP Dari Persamaan Linear Berikut Dg
Metode Campuran !
2x + 3y = 1 … pers.(1)
4x – 3y = 11 … pers.(2)
Jawab :
2x + 3y = 1
4x – 3y = 11 +
⇔ 6x = 12
⇔ x = 2
Harga x = 2 kmd substitusikan ke pers.(1) :
2x + 3y = 1
⇔ 2(2) + 3y = 1
⇔ 4 + 3y = 1
⇔ 3y = 1 – 4
⇔ 3y = - 3
⇔ y = - 1 Jd, HP = { 2, -1 }

19. 1) 5x + y = 5
17x + y = - 5 Jawab
2) 2p – 3q = 4
7p + 2q = 39 Jawab

20. 1) 5x + y = 5 … pers.(1)
17x + y = - 5 … pers(2)
5x + y = 5 Harga kmd
17x + y = - 5 - disubstitusikan ke pers(1) :
- 12x = 10 5x + y = 5
( x 6 )
⇔ - 25 + 6y = 30
⇔ 6y = 30 + 25
⇔ 6y = 55
6
5
12
10




x
6
5


x
5
6
5
5 )
( 


 y
5
6
25
)
( 


 y
6
1
9
6
55


 y
}
{
6
1
9
,
6
5


HP

21. 2) 2p – 3q = 4 … pers.(1)
7p + 2q = 39 … pers(2)
2p – 3q = 4 x 7 14p – 21q = 28
7p + 2q = 39 x 2 14p + 4q = 78 -
- 25q = - 50
2p – 3q = 4
⇔ 2p – 3(2) = 4
⇔ 2p – 6 = 4
⇔ 2p = 4 + 6
⇔ 2p = 10
⇔ p = 5
Jd, HP = { 5, 2 }
2
25
50




q

22. 4. Metode Determinan
Sistem persamaan, misalkan :
ax + by = c
px + qy = r
Menurut aturan determinan diubah mjd :
Artinya dan utk variabel x
dan y
didefinisikan :
,


q
p
b
a
p
b
q
a
q
p
b
a
.
. 



p
b
q
a
r
b
q
c
q
r
b
c
x
.
.
.
.





p
b
q
a
p
c
r
a
r
p
c
a
y
.
.
.
.






23. 4x – 5y = 22
7x + 3y = 15
Kita cari dl determinannya :
Jd, HP = { 3, -2}
3
47
141
47
75
66
47
15
)
5
(
3
.
22
3
15
5
22










x
47
35
12
7
)
5
(
3
.
4
3
7
5
4









2
47
94
47
154
60
47
7
.
22
15
.
4
15
7
22
4










y

25. 1) 2x – y = 2
3x – 2y = 1
Kita cari dl determinannya :
Jd, HP = { 3, 4}
3
1
3
1
1
4
1
1
)
1
(
)
2
(
2
2
1
1
2

















x
1
3
4
3
)
1
(
)
2
(
2
2
3
1
2













4
1
4
1
6
2
1
3
.
2
1
.
2
1
3
2
2












y

26. 2) 3x + 5y = 4
3x – y = 10
Kita cari dl determinannya :
Jd, HP = { 3, -1}
3
18
54
18
50
4
18
10
.
5
)
1
(
4
1
10
5
4















x
18
15
3
3
.
5
)
1
(
3
1
3
5
3











1
18
18
18
12
30
18
3
.
4
10
.
3
10
3
4
3












y