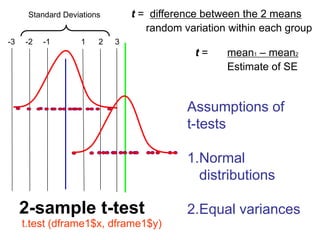
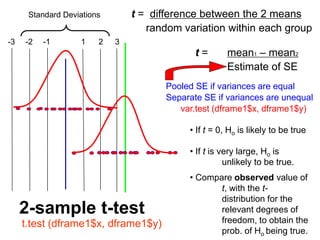
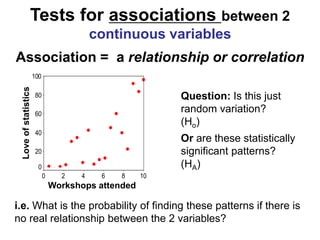
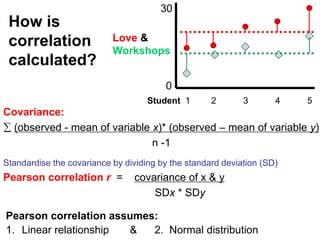
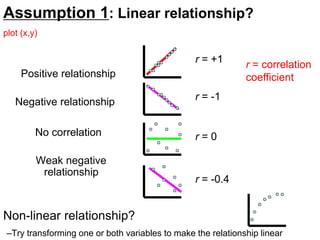
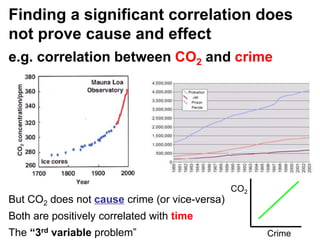
The document provides an overview of using R statistical software for data analysis, including steps to read and manipulate data, create visualizations, and perform statistical tests such as t-tests and correlation analyses. It covers descriptive statistics, hypothesis testing, and the importance of effect size and statistical power. The document also emphasizes the interpretation of results, including confidence intervals and correlation significance, while cautioning against inferring causation from correlation alone.

1. Data analysis with R
statistical software
Dr. Rob Thomas
 ThomasRJ@Cardiff.ac.uk
Session 1
Welcome to
the course

2. Getting started with R
Save the Excel file called “Heights.xls” as a .csv file
Excel > File > Save as > Save as type >
Choose “CSV (Comma delimited)
Save this file as “Heights.csv”
click on “OK” & “yes” when prompted
Open the R software on your computer
Ask R to read the heights.csv file
dframe1 <- read.csv(file.choose()) # navigate to your .csv file
names (dframe1) # names of the variables
summary (dframe1) # numerical summary

3. Histograms
with (dframe1, hist(Height))
hist (dframe1$Height)
Scatterplots
with (dframe1, plot(Age, Height))
plot (dframe1$Height~ dframe1$Age)
abline (lm (dframe1$Height~ dframe1$Age))
?plot # for help files about the “plot” function
Plotting graphs
–two ways of specifying variables

4. Pairwise plots
names(dframe1)
pairs (dframe1[c(1,2,4)],
panel = panel.smooth)
Specifies variables
1, 2 and 4 in
dframe1
Sex
130 150 170 190
1.0
1.2
1.4
1.6
1.8
2.0
130
150
170
190
Height
1.0 1.2 1.4 1.6 1.8 2.0 20 25 30 35
20
25
30
35
Age

5. Boxplots
…with or without a “notch”
boxplot (dframe1$Height)
boxplot (dframe1$Height~ Sex)
boxplot (dframe1$Height~ Sex, notch=T)
Female Male
130
140
150
160
170
180
190
Height
(cm)

6. Descriptive statistics
(i) Measures of location (averages)
• Arithmetic mean = sum / n =
mean (dframe1$Height, na.rm = T)
• Median = the middle value of a ranked dataset
median (dframe1$Height, na.rm = T)
• Sample size (N)
length (dframe1$Height)
- sum (is.na(dframe1$Height))

1
n
x
n

7. (ii) Measures of variability
Sum of squares = (observation – mean)2

0
1
2
…but the more data you have, the
bigger your measure of spread
Degrees of
freedom
Variance = sum of squares
n-1
var(dframe1$Height, na.rm=T))
…but the units are not the same as the original measurements
Mean

8. Standard deviation (SD) = square root of the variance
Sum of
squares
Degrees of
freedom
…units are the same
as the original
measurements
sqrt(var(dframe1$Height, na.rm = T))
or
sd (dframe1$Height, na.rm=T)

9. Standard error (SE) = standard deviation
n
A measure of how good our estimate of the mean is.
Surprisingly, R doesn’t have a ready-made function for
calculating SE, so we write our own function:
SD <- sd(dframe1$Height, na.rm = T)
N <- length(dframe1$Height) - sum(is.na(dframe1$Height))
SE <- SD/sqrt(N)
SE
The standard error is a useful descriptive statistic in itself,
but can also be used to calculate confidence intervals

10. Confidence Intervals (CI)
We are 95% confident that the true population mean lies within
the 95% CI limits
95% CI Limits = mean +/- (1.96 x SE)
99% CI Limits = mean +/- (2.58 x SE)
99.9% CI Limits = mean +/- (3.29 x SE)
lowerlimit <- (mean (dframe1$Height, na.rm = T) - 1.96*SE)
upperlimit <- (mean (dframe1$Height, na.rm = T) + 1.96*SE)
lowerlimit
upperlimit
interval.width <- upperlimit - lowerlimit
interval.width

11. Statistical hypothesis testing
All stats tests ask the same question:
“is the observed pattern real, or simply due to chance?”
Test statistic = Variance explained by the model .
Variance not explained by the model
P-value our estimate of the probability
of Ho being true
The aim of hypothesis testing is to distinguish between:
• Patterns caused by random variation in a sample (Ho)
• Real biological patterns -differences or associations (H1)
Evaluating results
• Biological effect size
• Statistical significance & statistical power
• Rejecting H1 does not mean that Ho must be true!

12. -1 1
-2 2
-3 3
Standard Deviations t = difference between the 2 means
random variation within each group
t = mean1 – mean2
Estimate of SE
2-sample t-test
t.test (dframe1$x, dframe1$y)
Assumptions of
t-tests
1.Normal
distributions
2.Equal variances

13. -1 1
-2 2
-3 3
Standard Deviations t = difference between the 2 means
random variation within each group
t = mean1 – mean2
Estimate of SE
• If t = 0, Ho is likely to be true
• If t is very large, Ho is
unlikely to be true.
• Compare observed value of
t, with the t-
distribution for the
relevant degrees of
freedom, to obtain the
prob. of Ho being true.
Pooled SE if variances are equal
Separate SE if variances are unequal
var.test (dframe1$x, dframe1$y)
2-sample t-test
t.test (dframe1$x, dframe1$y)

14. How does a
t-test work?
Exercise:
The Dr Ian Vaughan
Memorial Spreadsheet
The master at work:
Ian collecting data for his next t-test
Excel file in:
Session 1 folder
Left hand side:
Checking for normal distributions
Checking for homogeneity of variances
Right hand side:
t-test for equal variances
t-test for unequal variances

15. Reporting a t-test
There are 5 things that you must ALWAYS state when reporting a
statistical test:
1. Name of the test E.g. 2-sample t-test
1-tailed or 2-tailed test? 2-tailed test
2. Value of the test statistic t = 5.164
3. Sample sizes n = 119, 186
or degrees of freedom d.f. = 303
4. Statistical significance P < 0.0001
i.e. a significant difference between male and female heights
5. Effect size and direction (means ± Confidence Intervals)
Males = 168.2cm (166.5-169.8), Females = 159.8cm (158.1-161.3)

16. Things to consider when evaluating
the test of a hypothesis
1. Effect size
Is the size of the effect important?
2. Statistical significance
P = probability the Ho is true
Accept or reject Ho
P = 0.05 is the conventional cut-off between significant
and non-significant effects, but this is arbitrary!
e.g. P = 0.0499 is marginally significant
but P = 0.0501 is marginally non-significant
…even though these 2 results are nearly identical
3. Statistical power

17. Lectures attended
10
8
6
4
2
0
100
80
60
40
20
0
No. of stats workshops attended
18
16
14
12
10
8
6
4
2
0
30
25
20
15
10
5
0
Workshops attended
Love
of
statistics
Question: Is this just
random variation?
(Ho)
Or are these statistically
significant patterns?
(HA)
Association = a relationship or correlation
i.e. What is the probability of finding these patterns if there is
no real relationship between the 2 variables?
Tests for associations between 2
continuous variables

18. How is
correlation
calculated?
Pearson correlation assumes:
1. Linear relationship & 2. Normal distribution
Covariance:
 (observed - mean of variable x)* (observed – mean of variable y)
n -1
Standardise the covariance by dividing by the standard deviation (SD)
Pearson correlation r = covariance of x & y
SDx * SDy
Student 1 2 3 4 5
Love &
Workshops
0
30

19. plot (x,y)
Positive relationship
Negative relationship
No correlation
Weak negative
relationship
Non-linear relationship?
–Try transforming one or both variables to make the relationship linear
Assumption 1: Linear relationship?
r = +1
r = -1
r = 0
r = -0.4
r = correlation
coefficient

20. Assumption 2: Normal distributions?
If the data are normally distributed, or can be transformed
(squashed) to be normally distributed, use a
Pearson’s correlation
Otherwise, use a Spearman’s rank correlation
…or a Kendall’s tau correlation with small sample sizes (n<7)
and/or lots of tied ranks
How to test for correlations
To do a Pearson correlation:
cor.test (dframe1$x, dframe1$y)
To do a Spearman rank or Kendall’s tau correlation:
cor.test (dframe1$x, dframe1$y, method = “spearman”)
cor.test (dframe1$x, dframe1$y, method = “kendall”)

21. Reporting correlations
There are 6 things that you must ALWAYS state when reporting a
statistical test:
1. Name of the test E.g. Pearson’s correlation
2. 1-tailed or 2-tailed test? 2-tailed test
3. Value of the test statistic r = 0.789
4. Sample size n = 18
or degrees of freedom d.f. = 16
5. Statistical significance P < 0.0001
i.e. a highly significant positive correlation
6. Effect size (note that the correlation coefficient r is also a
measure of the effect size / strength of the relationship)

22. The meaning of r2
= the proportion of the variation in one variable that
is “explained” by variation in the other.
e.g. Correlation between love of statistics
and attendance
r = 0.789
r2 = 0.623
…so 0.623 (i.e. 62.3%) of the variation in love of
statistics “explained by” variation in attendance
N.B. r2 is only meaningful for Pearson’s correlation r,
not for Spearman’s rank or Kendall’s tau correlations

23. Finding a significant correlation does
not prove cause and effect
e.g. correlation between CO2 and crime
But CO2 does not cause crime (or vice-versa)
Both are positively correlated with time
The “3rd variable problem”
CO2
Crime

24. e.g. correlation between cannabis use
& psychological problems
Does cannabis use cause psychological problems?
Or do psychological problems cause cannabis use?
Or is there a 3rd variable (e.g. income?)
that happens to be correlated with both?
Correlations can highlight areas
for experimental research