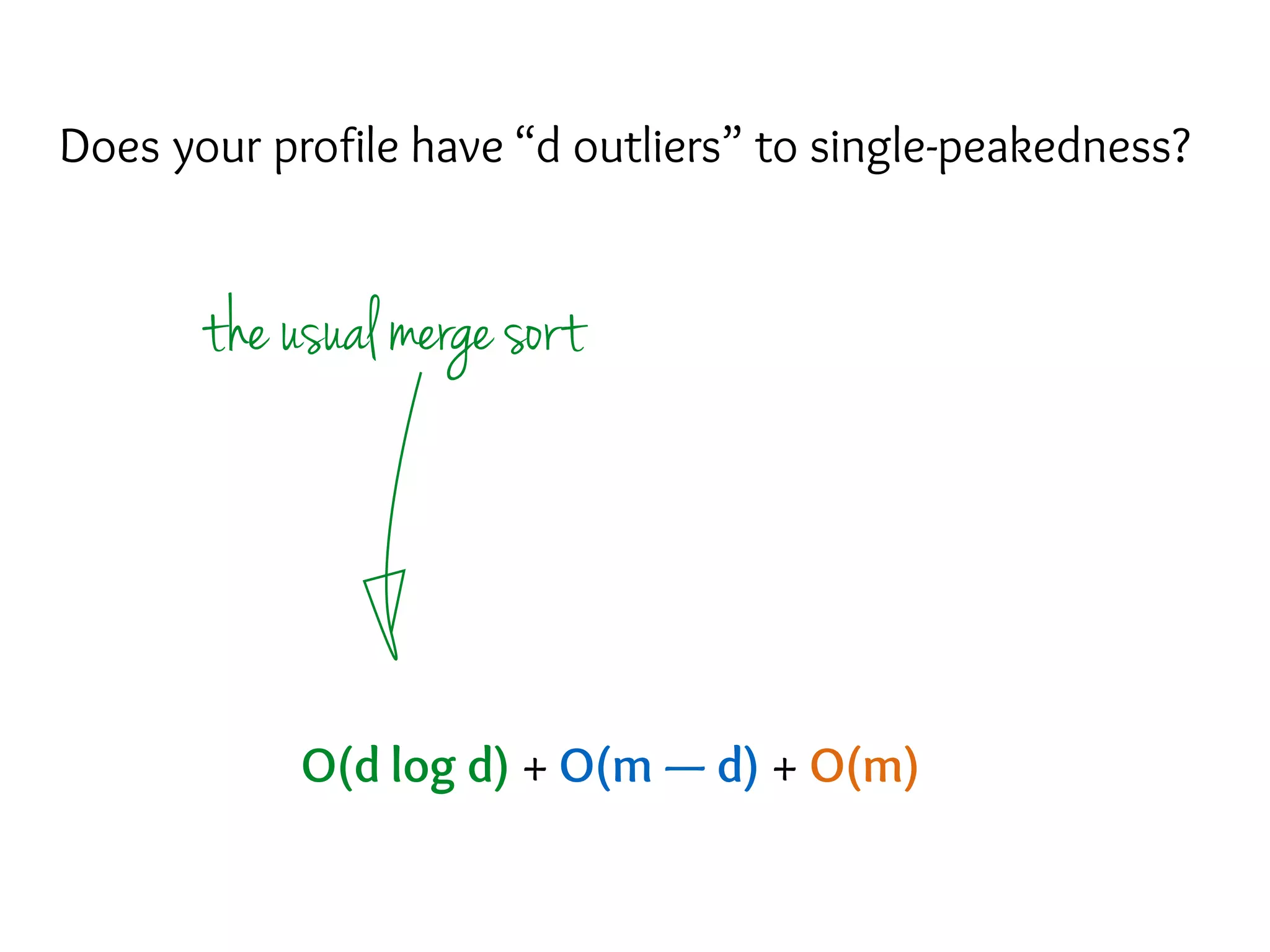
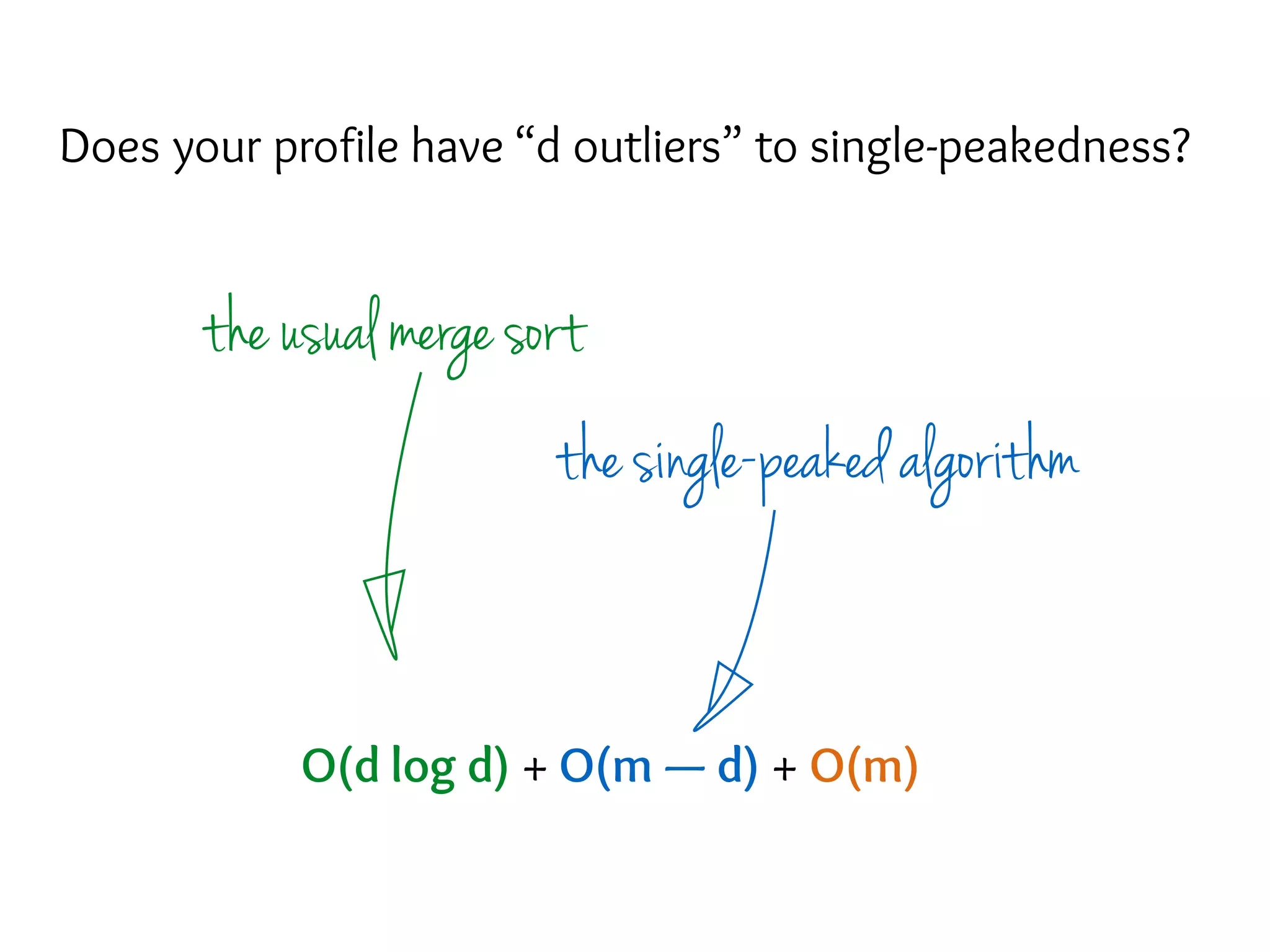
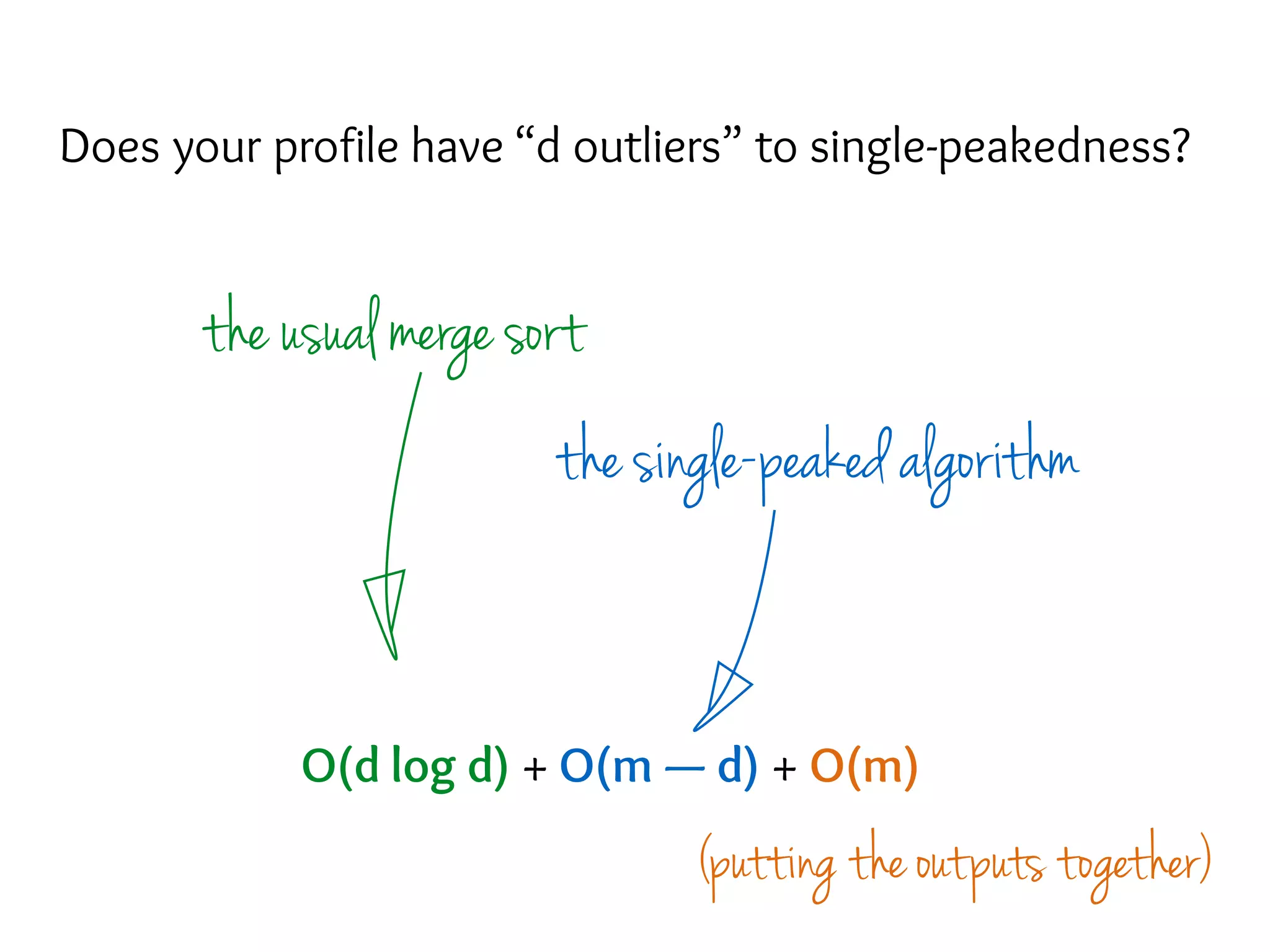
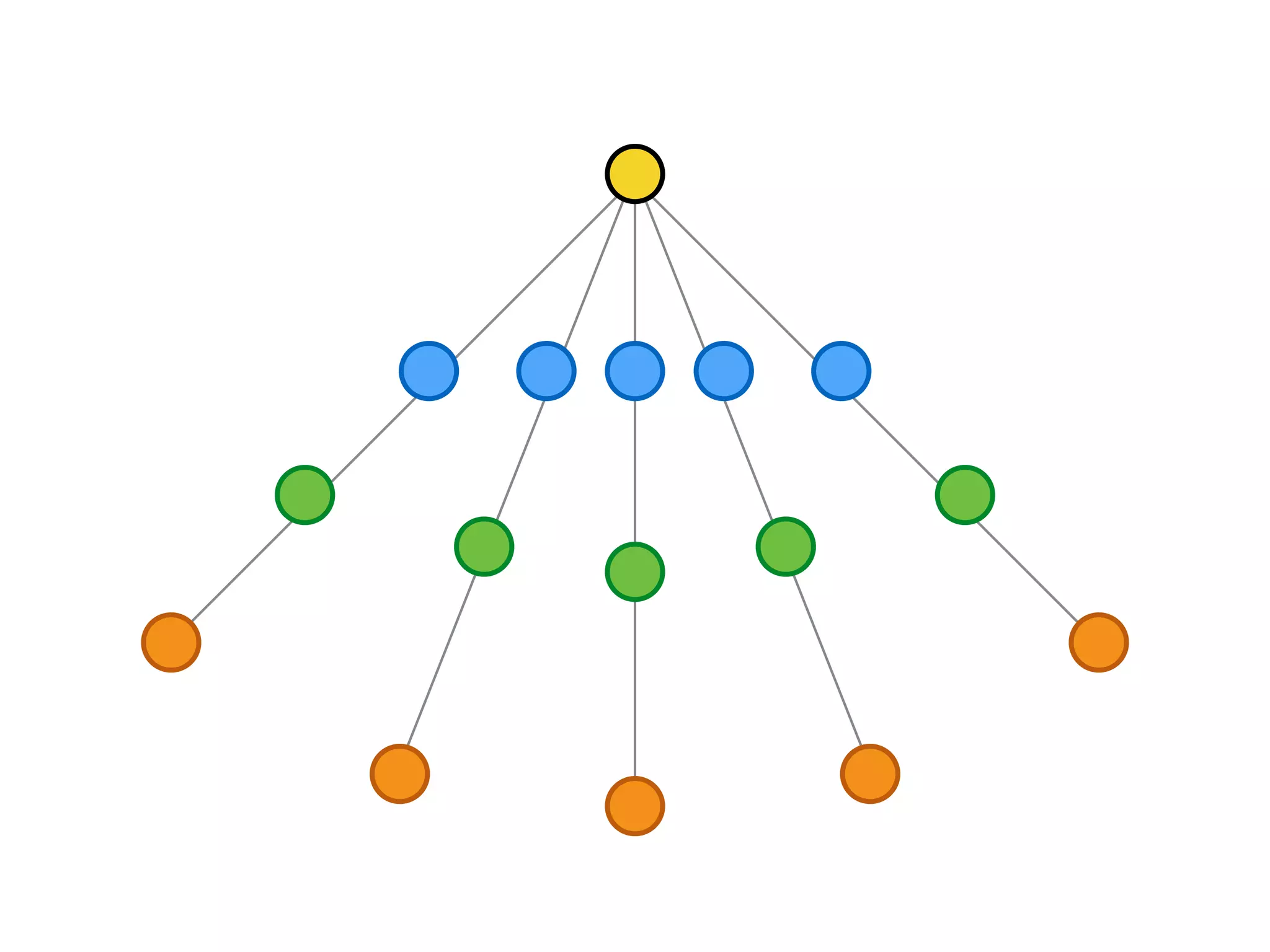
The document discusses eliciting single-peaked preferences over trees, focusing on the query model for preference elicitation and complexities involved. It outlines the advantages of single-peaked preferences, such as having no Condorcet cycles and being easily identifiable, while describing improved querying strategies to reconstruct full preferences through comparison queries. The main strategy involves splitting the preference tree into paths, processing each path, and merging results, achieving efficient query complexities.







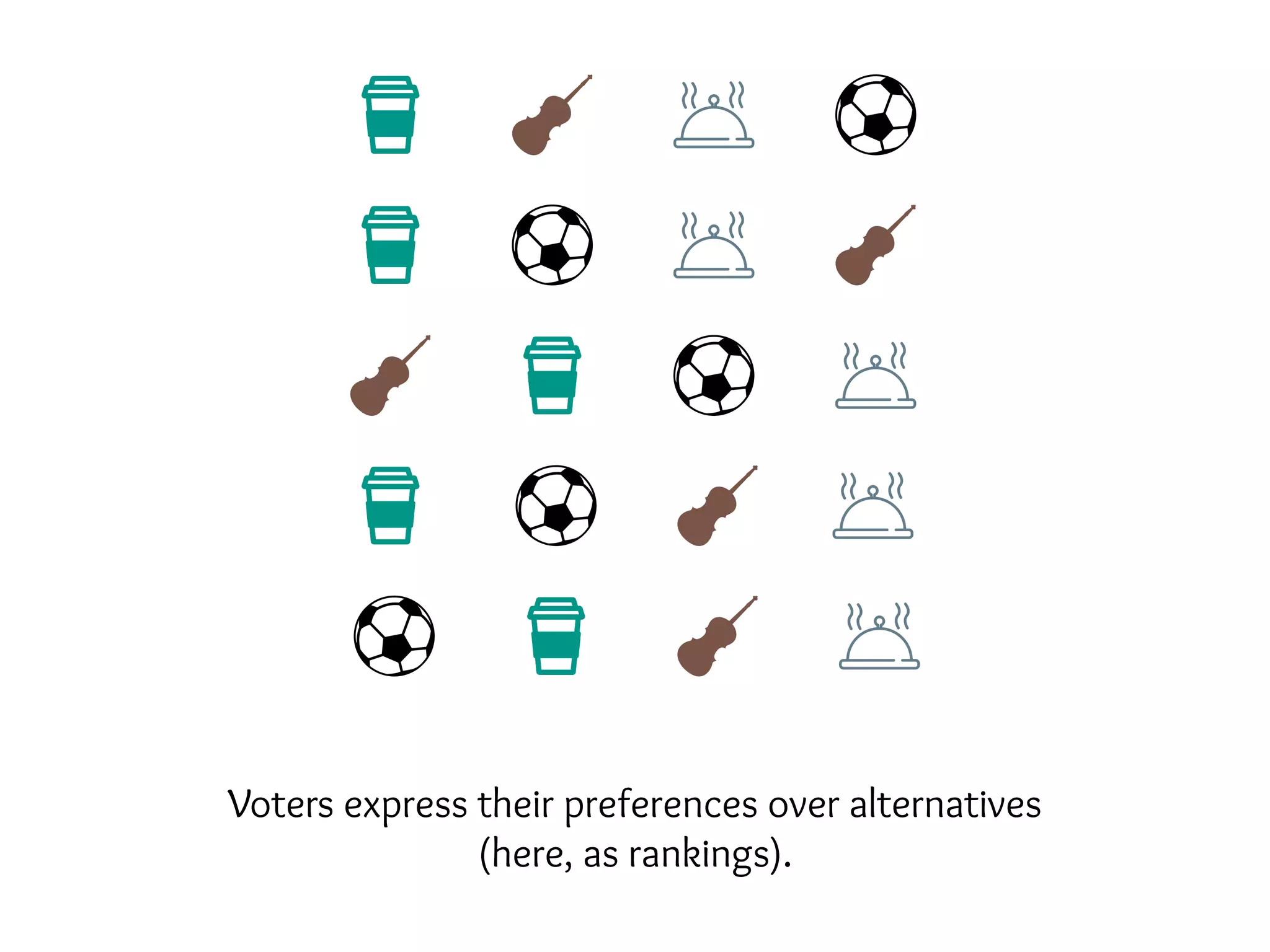
















![Single Peaked Preferences
and better query complexities for elicitation. [1]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-29-2048.jpg)




![Left RightCenter
A B C D E F G
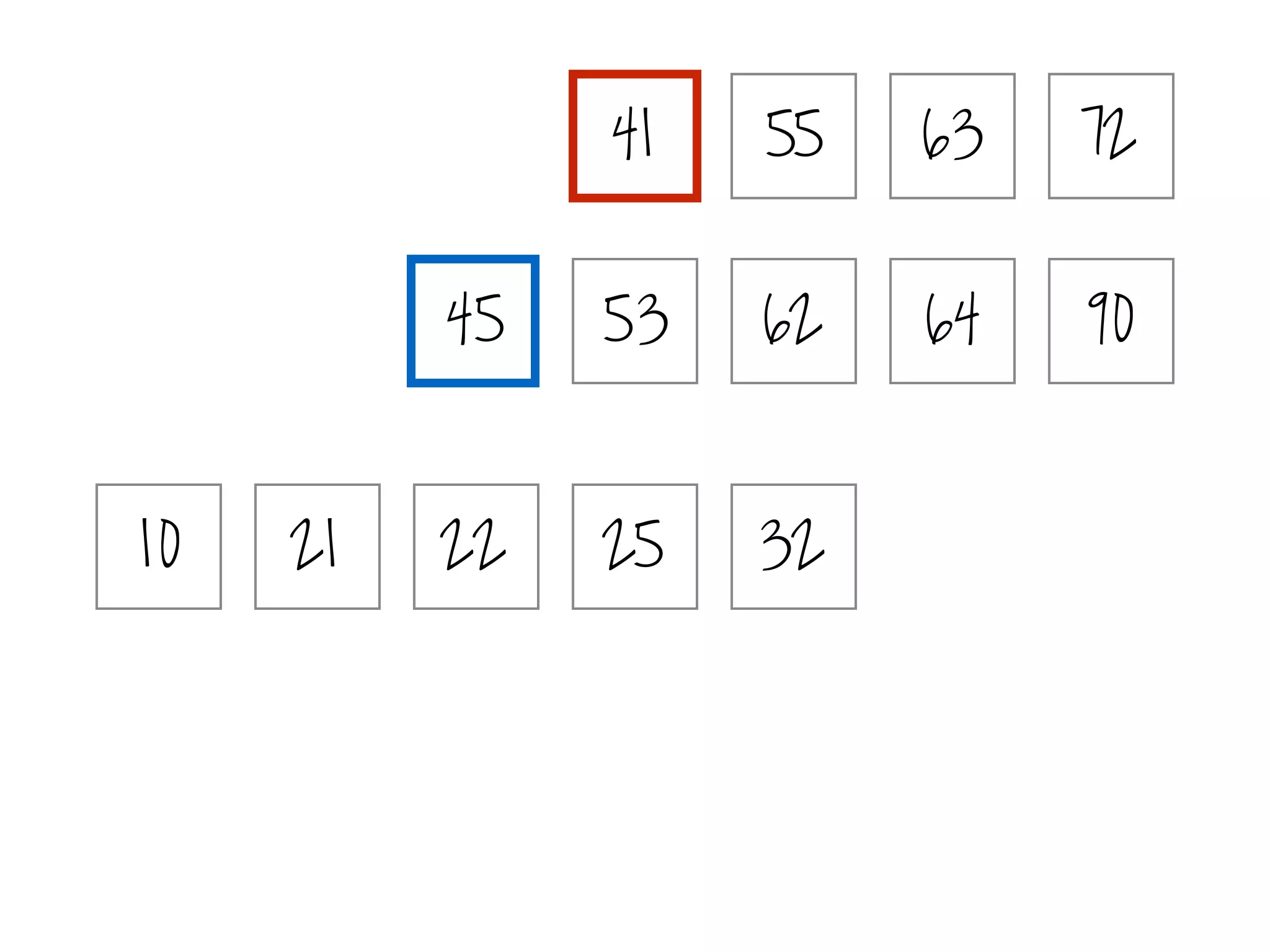
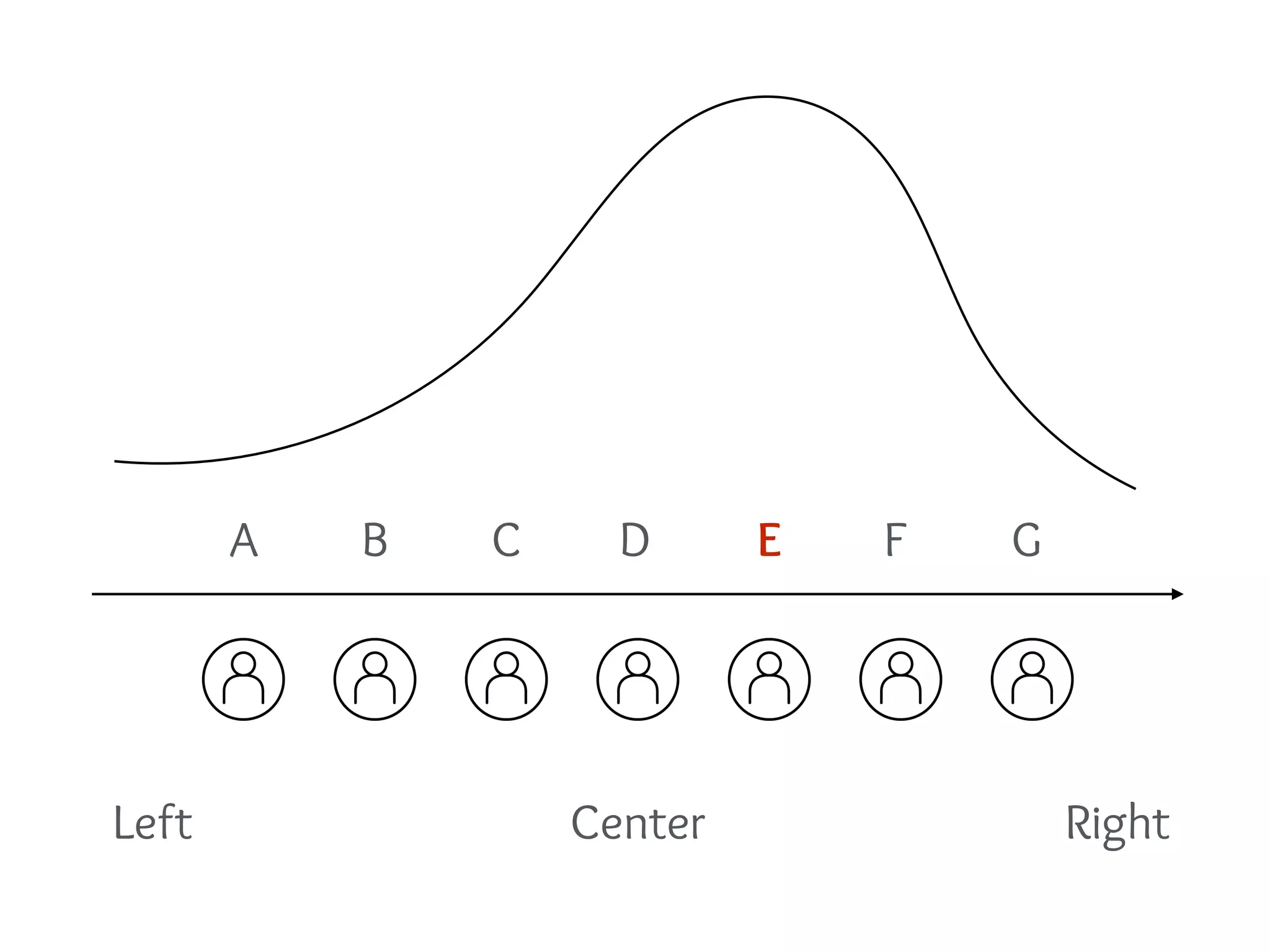
(i) Identify the peak: use binary search.
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-41-2048.jpg)
![Left RightCenter
A B C D
E
F G
(i) Identify the peak: use binary search.
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-42-2048.jpg)
![Left RightCenter
A B C D
E
F G
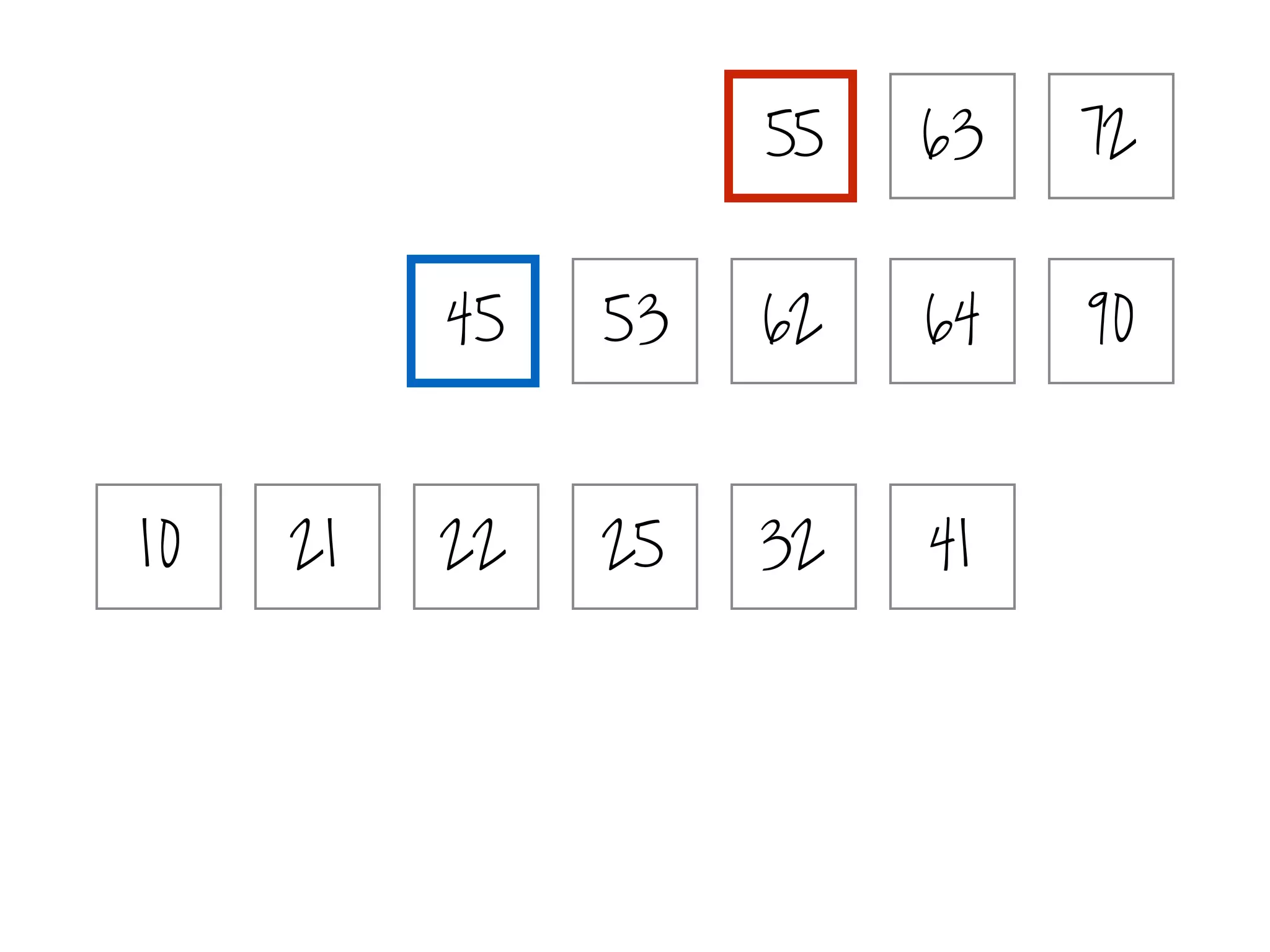
(i) Identify the peak: use binary search.
this signals that the
peak is to the right.
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-43-2048.jpg)
![Left RightCenter
A B C D E F G
(i) Identify the peak: use binary search.
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-44-2048.jpg)
![Left RightCenter
A B C
D
E F G
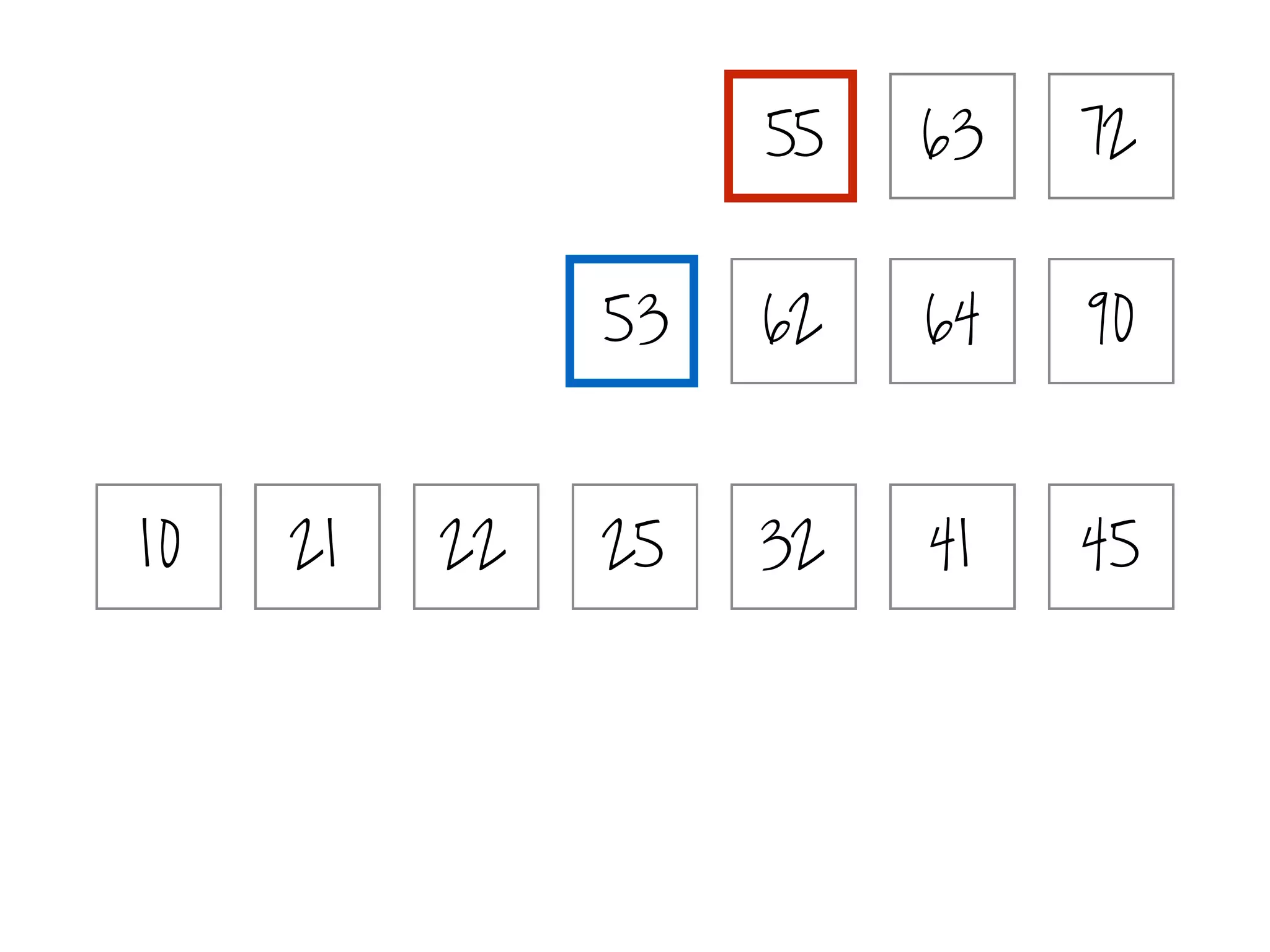
(i) Identify the peak: use binary search.
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-45-2048.jpg)
![Left RightCenter
A B C
D
E F G
(i) Identify the peak: use binary search.
this signals that the
peak is to the left.
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-46-2048.jpg)
![Left RightCenter
A B C D E F G
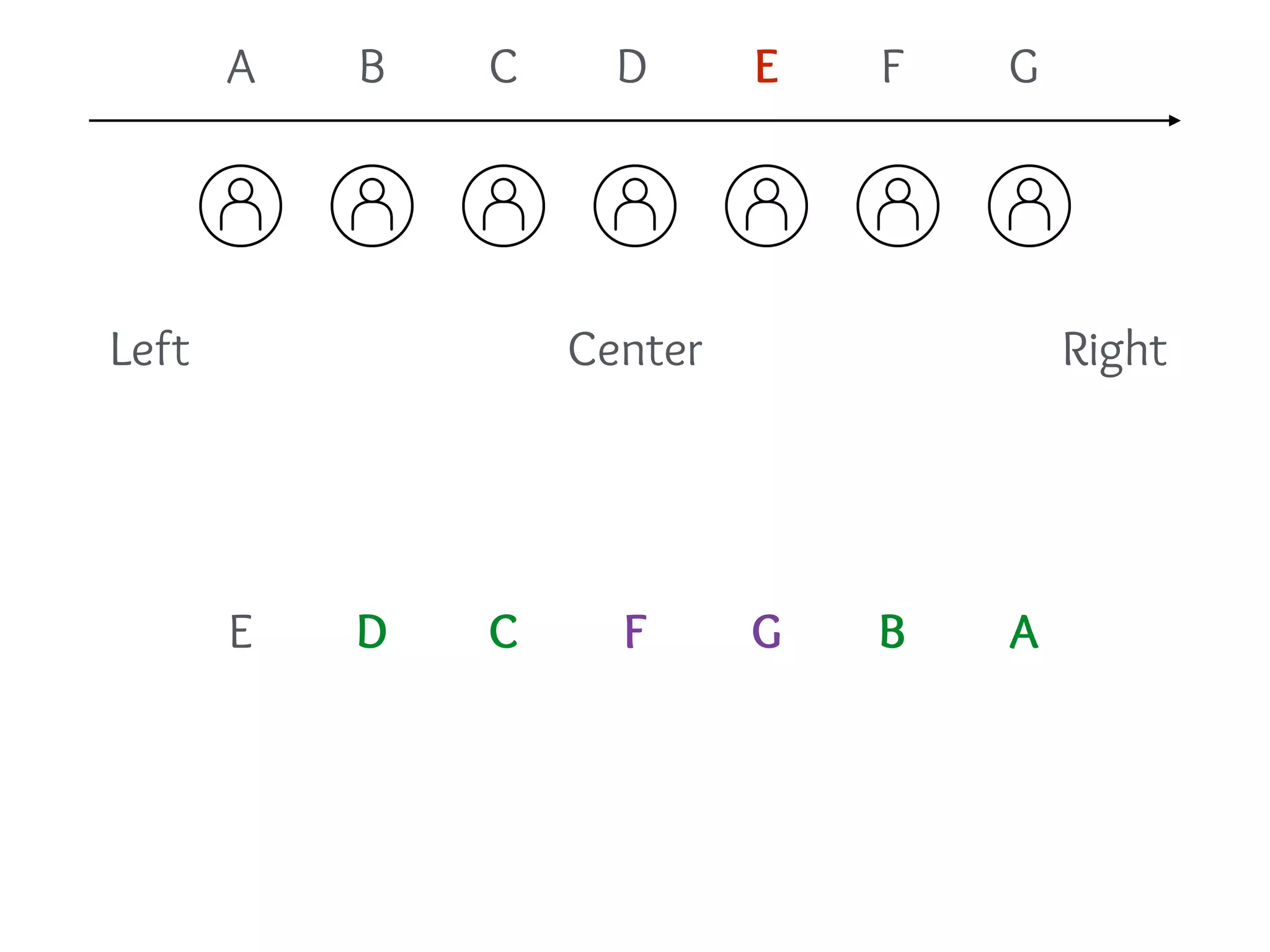
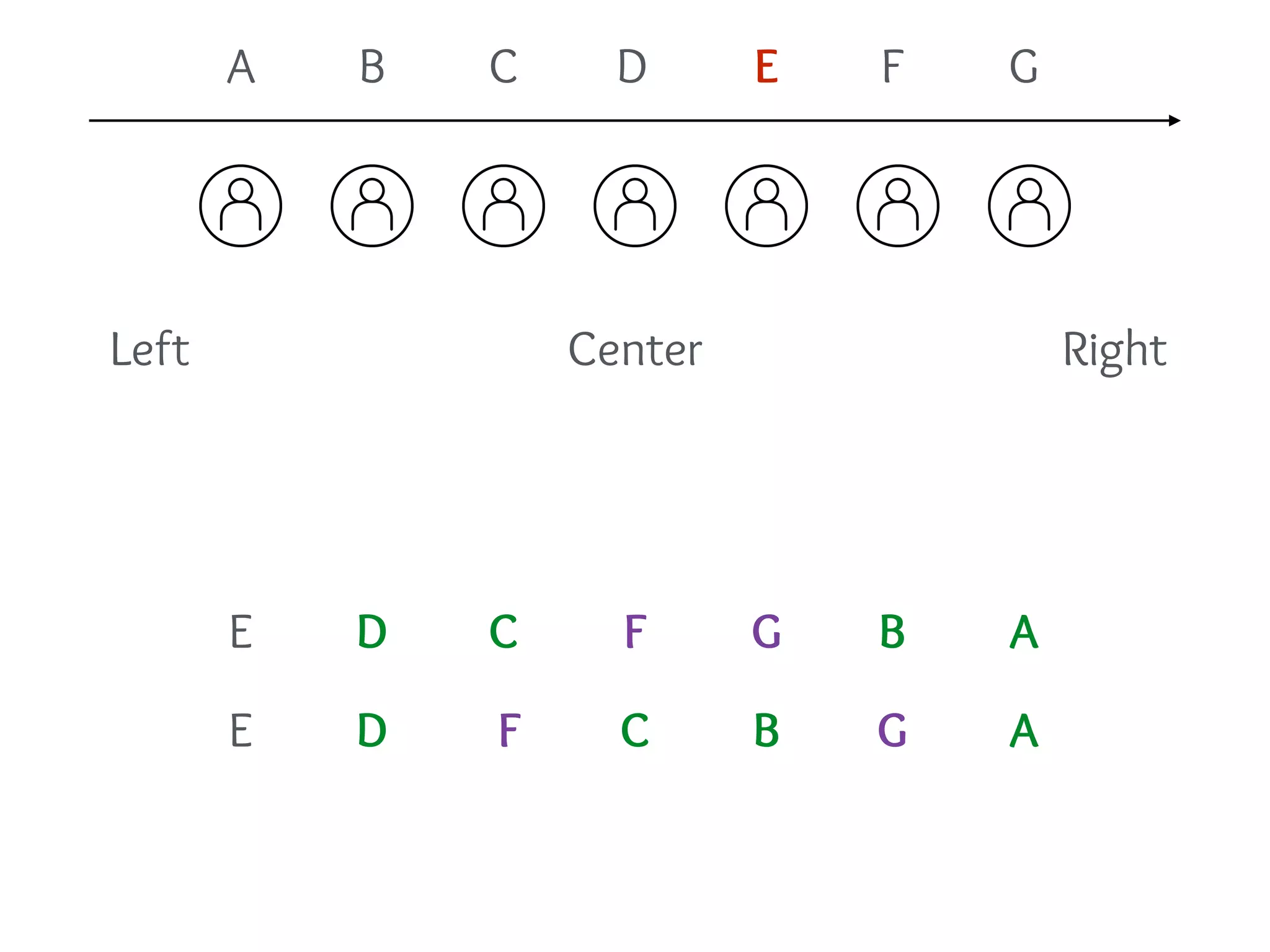
(ii) Once we know the peak, the rest is O(m) queries.
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-47-2048.jpg)
![Left Right
A B C D E F G
(ii) Once we know the peak, the rest is O(m) queries.
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-48-2048.jpg)
![Left Right
A B C D E F G
(ii) Once we know the peak, the rest is O(m) queries.
C
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-49-2048.jpg)
![Left Right
A B C D E F G
(ii) Once we know the peak, the rest is O(m) queries.
C
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-50-2048.jpg)
![Left Right
A B C D E F G
(ii) Once we know the peak, the rest is O(m) queries.
C
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-51-2048.jpg)
![Left Right
A
B
C D E F G
(ii) Once we know the peak, the rest is O(m) queries.
C
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-52-2048.jpg)
![Left Right
A
B
C D E F G
(ii) Once we know the peak, the rest is O(m) queries.
C
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-53-2048.jpg)
![Left Right
A B C D E F G
(ii) Once we know the peak, the rest is O(m) queries.
C
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-54-2048.jpg)
![Left Right
A B C
D
E F G
(ii) Once we know the peak, the rest is O(m) queries.
C
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-55-2048.jpg)
![Left Right
A B C
D
E F G
(ii) Once we know the peak, the rest is O(m) queries.
C
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-56-2048.jpg)
![Left Right
A B C D E F G
Center
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-57-2048.jpg)
![Left Right
A B C D E F G
Center
(ii) Once we know the peak, the rest is O(m) queries.
(i) Identify the peak: use binary search (O(log m) queries).
[Better query complexities for elicitation.]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-58-2048.jpg)
![GeneraliZing “single-Peakedness”
so we consider broader domains but still have nice properties. [2]](https://image.slidesharecdn.com/duke-august2016-prefelicitation-200521164347/75/Elicitation-for-Preferences-Single-Peaked-on-Trees-59-2048.jpg)