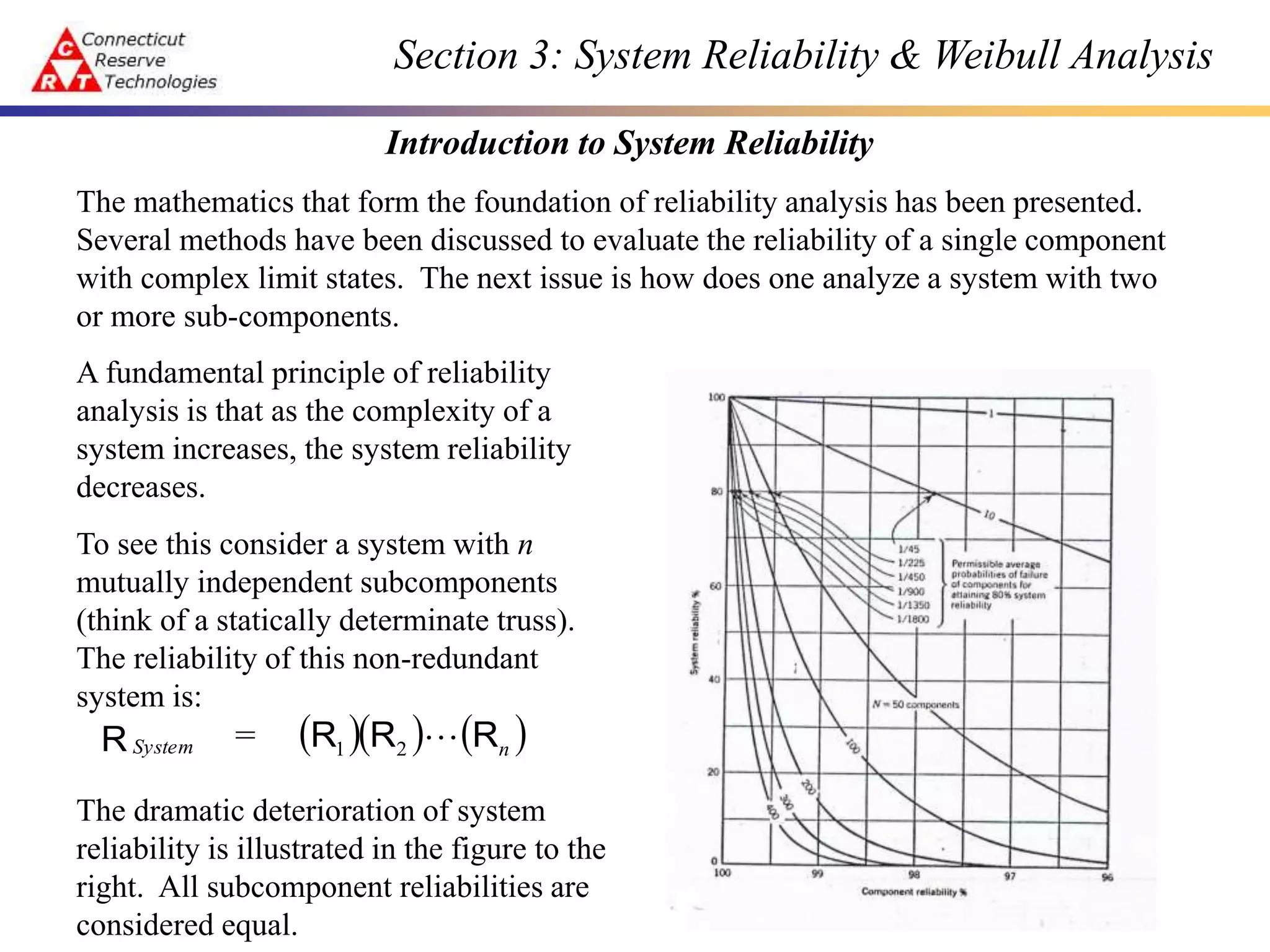
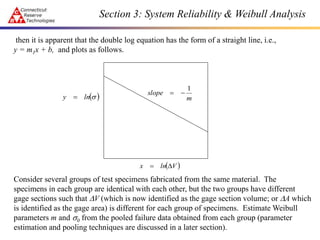
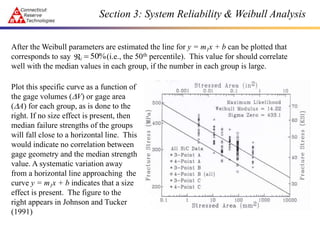
This document discusses system reliability and Weibull analysis. It introduces system reliability principles, including how reliability decreases as complexity increases. Series systems are discussed as having the reliability of the weakest link. The Weibull distribution is presented as a good model for brittle failure in ceramics. A two-parameter Weibull distribution accounts for size effects through a characteristic strength that depends on specimen geometry. Component reliability is derived by treating a continuum of elements as a series system and integrating their failure probabilities.