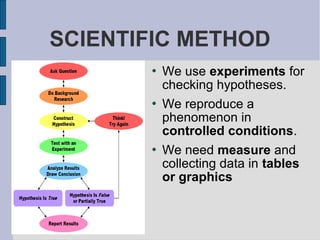
The document discusses physics and chemistry, comparing what they have in common (studying matter) and what makes them different (physics studies phenomena that don't change matter composition, while chemistry studies phenomena that do change composition). It then provides an overview of the scientific method, including making observations and asking questions, developing hypotheses to test, conducting controlled experiments, analyzing results, and drawing conclusions. Finally, it covers scientific concepts like units, measurements, errors, and notation.

1. Unit 1
THE SCIENTIFIC WORK

2. Physics and Chemistry

What do they have in common?

Physicists and Chemists study
the same: matter.

Physicists, Chemists and other
scientists work in the same way:

SCIENTIFIC METHOD

3. Physics and Chemistry

What makes them different?

Physics studies
phenomena that don't
change the
composition of matter.

Chemistry studies
phenomena that change
the composition of
matter.

4. SCIENTIFIC METHOD

5. SCIENTIFIC METHOD
 The observation of a
phenomenon and
curiosity make
scientists ask
questions.
 Before doing anything
else, it's necessary to
look for the previous
knowledge about the
phenomenon.

6. SCIENTIFIC METHOD
 Hypotheses are
possible answers to
the questions we
asked.
 They are only
testable predictions
about the
phenomenon.

7. SCIENTIFIC METHOD
 We use experiments for
checking hypotheses.
 We reproduce a
phenomenon in
controlled conditions.
 We need measure and
collecting data in tables
or graphics

8. SCIENTIFIC METHOD
 We study the relationships
between different
variables.
 In an experiment there are
three kinds of variables
− Independent
variables: they can be
changed.
− Dependent variables:
they are measured.
− Controlled variables:
they don't change.

9. SCIENTIFIC METHOD
 After the experiment, we
analyse its results and
draw a conclusion.
 If the hypothesis is true,
we have learnt
something new and it
becomes in a law
 If the hypothesis is false.
We must look for a new
hypothesis and continue
the research.

10. Magnitudes,
measurements and units

Physical Magnitude: It refers to every
property of matter that can be measured.
− Length, mass, surface, volume, density,
velocity, force, temperature,...

Measure: It compares a quantity of a
magnitude with other that we use as a
reference (unit).

Unit: It is a quantity of a magnitude used to
measure other quantities of the same
magnitude. It's only useful if every people uses
the same unit.

11. Magnitudes,
measurements and units
Length of the classroom = 10 m
means
The length of the classroom is 10 times the
length of 1 metre.

12. The International System
of Units

The SI has:
− a small group of magnitudes whose units
are fixed directly: the fundamental
magnitudes.

E.g.: Length → meter (m); Time → second
(s)
− The units for the other magnitudes are
defined in relationship with the fundamental
units: the derivative magnitudes.

E. g.: speed → meter/second (m/s)

13. The International System
of Units
The fundamental magnitudes and their units
Length meter m
Mass kilogram kg
Time second s
Amount of substance mole mol
Temperature Kelvin K
Electric current amperes A
Luminous intensity candela cd

14. The International System
of Units
Some examples of how to build the units of derivative
magnitudes:
− Area = Length · width → m·m = m2
− Volume = Length · width · height → m·m·m =
m3
− Speed = distance / time → m/s
− Acceleration = change of speed / time →
(m/s)/s = m/s2

15. The International System
of Units
Some examples of how to build the units of derivative
magnitudes:
− Area = Length · width → m·m = m2
− Volume = Length · width · height → m·m·m =
m3
− Speed = distance / time → m/s
− Acceleration = change of speed / time →
(m/s)/s = m/s2

16. The International System
of Units
More derivative units.
Quantity Name Symbol
Area square meter
m2
Volume cubic meter m3
Force Newton N
Pressure Pascal Pa
Energy Joule J
Power Watt W
Voltage volt V
Frequency Hertz Hz
Electric charge Coulomb C

17. The International System
of Units
Prefixes: we used them when we need express quantities
much bigger or smaller than basic unit.
Power of 10 for
Prefix Symbol Meaning Scientific Notation
_______________________________________________________________________
mega- M 1,000,000 106
kilo- k 1,000 103
deci- d 0.1 10-1
centi- c 0.01 10-2
milli- m 0.001 10-3
micro- µ 0.000001 10-6
nano- n 0.000000001 10-9

18. The International System
of Units
Prefixes: the whole list
Factor Name Symbol Factor Name Symbol
10-1 decimeter dm 101 decameter dam
10-2 centimeter cm 102 hectometer hm
10-3 millimeter mm 103 kilometer km
10-6 micrometer µm 106 megameter Mm
10-9 nanometer nm 109 gigameter Gm
10-12 picometer pm 1012 terameter Tm
10-15 femtometer fm 1015 petameter Pm
10-18 attometer am 1018 exameter Em
10-21 zeptometer zm 1021 zettameter Zm
10-24 yoctometer ym 1024 yottameter Ym

19. Changing units

We can change a quantity into another unit.
Conversion factors help us to do it.

A conversion factor is a fraction with the
same quantity in its denominator and in its
numerator but expressed in different units.
1h 1 km
=1 =1
60 min 1000 m
60 min 1000 m
=1 =1
1h 1 km

20. Changing units
Let's see a few examples of how to use them
1 km 2570 km ·1
2570 m · = =2,570 km
1000 m 1000
1 h 1 min 3500 h
3500 s · · = =0,972 h
60 min 60 s 3600
2

500 cm² ·
1m
100 cm 
=500 cm² · 
1m²
10000 cm²
= 
500 m²
10000
=0,05 m²
m m 1 km 3600 s 30 · 3600 km km
30 =30 · · = =108
s s 1000 m 1 h 1000 h h

21. Significant figures
•
They indicate precision of a measurement.
•
Sig Figs in a measurement are the really
known digits.
2.3 cm

22. Significant figures

Counting Sig Figs:
− Which are sig figs?

All nonzero digits.

Zeros between nonzero digits
− Which aren't sig figs?

Leading zeros – 0,0025

Final zeros without
a decimal point – 250

Examples:
− 0,00120 → 3 sig figs; 15000 → 2 sig figs
− 15000, → 5 sig figs; 13,04 → 4 sig

23. Significant figures

Calculating with sig figs
− Multiplicate or divide: the factor with the
fewer number of sig figs determines the
number of sig figs of the result:

2,345 m · 4,55 m = 10,66975 m 2 = 10,7 m2

(4 sig figs) (3 sig figs) → (3 sig figs)
− Add or substract: the number with the
fewer number of decimal places
determines the number of decimal places
of the result:

3,456 m + 2,35 m = 5,806 m = 5,81 m

(3 decimal places) (2 decimal places) → (2 decimal places)

24. Significant figures

Calculating with sig figs
− Exact number have no limit of sig fig:

Example: Area = ½ · Base · height.

½ isn't taken into account to round the
result.
− Rounding the result:

If the first figure is 5, 6, 7, 8 or 9, the last
figure taken into account is increased in 1

If not, it doesn't change.

25. Scientific notation

Is used to write very large or very small quantities:
− 385 000 000 Km = 3.85·108 Km
− 0,000 000 000 157 m = 1,57·10-10 m

Changing a number to scientific notation:
− We move the decimal point until there is an only
number in its left side.
− The exponent of 10 is the number of places we
moved the decimal point:

The exponent is positive if we move it to the left side

It's negative if we move it to the right side.

26. Measurement errors

It's impossible to measure a quantity with
total precision.

When we measure, we'll never know the
real value of the quantity.

Every measurement has an error because:
− The measurement instrument can only see
a few sig figs.
− It may not be well built or calibrated.
− We are using it in the wrong way.

27. Measurement errors

There are two ways for expressing the error
of a measurement:
− Absolute error: it is the difference
between the value of the measurement and
the value accepted as exact.
− Relative error: it is the absolute error in
relationship with the quantity.

28. Measurement errors

How to calculate the error. EXAMPLE 1:
− We have measured several times the mass of a
ball:

20,17 g, 20,21 g, 20,25 g, 20,15 g, 20,28 g
− It's supposed that the real value of the ball of the
mass is the average value of all the
measurements:

Vr = (20,17 g + 20,21 g + 20,25 g + 20,15 g + 20,27 g )/5 = 20,21 g
− The absolute error of the first measurement is:

Er = |20,17 g – 20,21 g| = 0,04 g
− The relative error is calculate dividing the absolute
error by the value of quantity.

29. Measurement error

How to calculate the error. EXAMPLE 2:
− We have measured once the length of a
piece of paper using a ruler that is
graduated in millimetres: 29,7 cm
− We suppose that the real value is the
measured value.
− The absolute error is the precision of the
rule:
 Ea = 0,1 cm
− Relative error:

Er = 0,1 cm / 29,7 cm = 0,0034 = 0,34 %