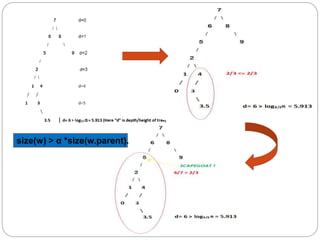
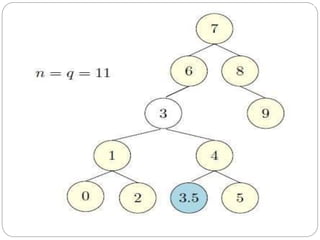
The scapegoat tree is a self-balancing binary search tree that achieves O(log n) time for search, insert, and delete operations. It works by occasionally selecting an unbalanced "scapegoat" node and rebuilding its subtree to rebalance the tree. The scapegoat is identified when a node's size is more than an alpha value times its parent's size. The subtree rooted at the scapegoat is then rebuilt by converting its inorder traversal to a new balanced binary search tree.

1. Presented by
Sams Uddin Ahamed
&
Najmus Sakib Borson
Scapegoat Tree
(Data Structure)

2. What is Scapegoat?
 The scapegoat tree is an implementation of a
self-balancing binary tree. This structure is based
on the common wisdom that when something
goes wrong, the first thing people tend to do is
find someone to blame as known as scapegoat.
Once blame is firmly established, we can leave
the scapegoat to fix the problem.
 Time complexity
-Search in O(log n) worst-case time
- Insert/delete in O(log n) amortized(average) time
-Starting with an empty scapegoat tree, a
sequence of m insertions and deletions takes
O(mlog n) .

3. Theorem
A binary search tree is said to be weight balanced if half
of nodes are on the left of the root and half on the right.
An α weight balanced node is therefore:
size(left) <= α *size(node)
size(right) <= α *size(node)
Value of Alpha
The α for a scapegoat tree can be any number between
0.5 to 1. A high α value results in fewer balances,
making insertion quicker but searching and deletions
slower, and vice versa for a low α .

4. How It works?
 Step 1
At first we have to find the scapegoat for which
the tree is unbalanced. To find the scapegoat we use
α(.5< α<1) which is the ratio of Parent and child node.
 Step 2
After finding the scapegoat we have to rebuild
the sub-tree rooted at the scapegoat node.

5. Properties
Insertion (Assuming α = 2/3 =0.67):
To insert value x in a Scapegoat Tree:
 Create a new node u and insert x using the BST
insert algorithm.
 If the depth of u is greater than log3/2n where n is
number of nodes in tree then we need to make
tree balanced. To make balanced, we use below
step to find a scapegoat.
 Walk up from u until we reach a node w with size(w)
> (2/3)*size(w.parent). This node is scapegoat.
 Rebuild the subtree rooted at w.parent.

6. size(w) > α *size(w.parent).

8. Delete
To remove the value x from a Scapegoat Tree:
 run the standard deletion algorithm for binary
search trees
 decrement n (where n= number of nodes)
 if n < q/2 (where q is overestimate of n) then
- rebuild the entire tree and set q=n
Search
 The Search operation in Scapegoat tree is done
like regular Search in a binary search tree.

9. Rebuild
In rebuilding, we simply convert the subtree to the most
possible balanced BST. We first store inorder traversal of
BST in an array, then we build a new BST from array by
recursively dividing it into two halves.
Time complexity of Rebuild
The actual process of re-balancing the tree rooted at
the scapegoat takes O(n)time. However, this is not a
fair analysis because while the scapegoat could be
the root of the tree, it could also be a node very deep
in the tree. That process would much faster because
the vast majority of the tree is left alone. Therefore,
the re-balancing process takes O(log
n) amortized(average) time.

10.  Advantages
The scapegoat tree is the first binary search
tree to achieve its complexity without storing
extra information at every node. This saves large
amounts of space, making it an attractive
balanced binary search tree.
 Disadvantages
Lazy data structure. Only does work when
search paths get too long.