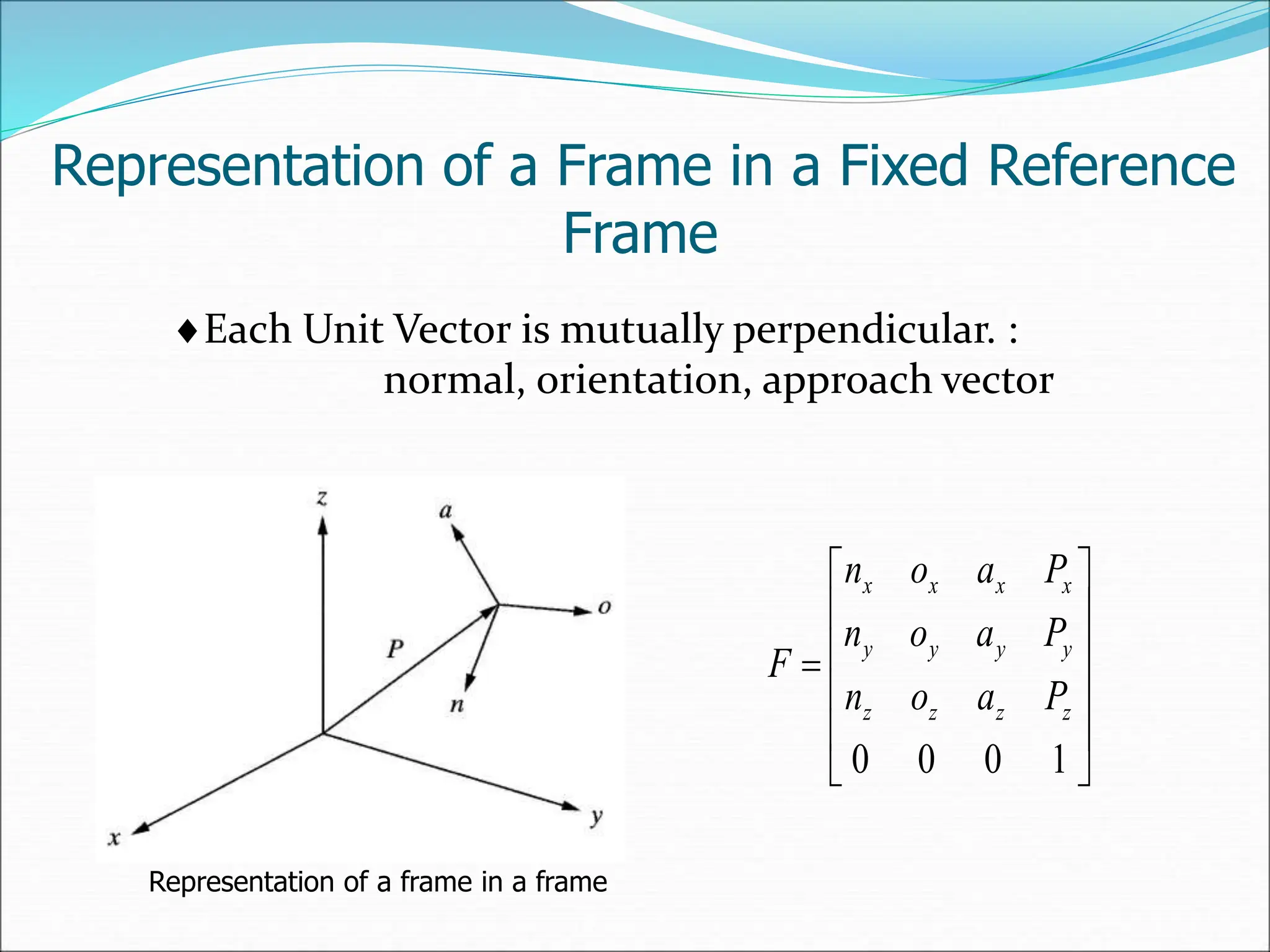
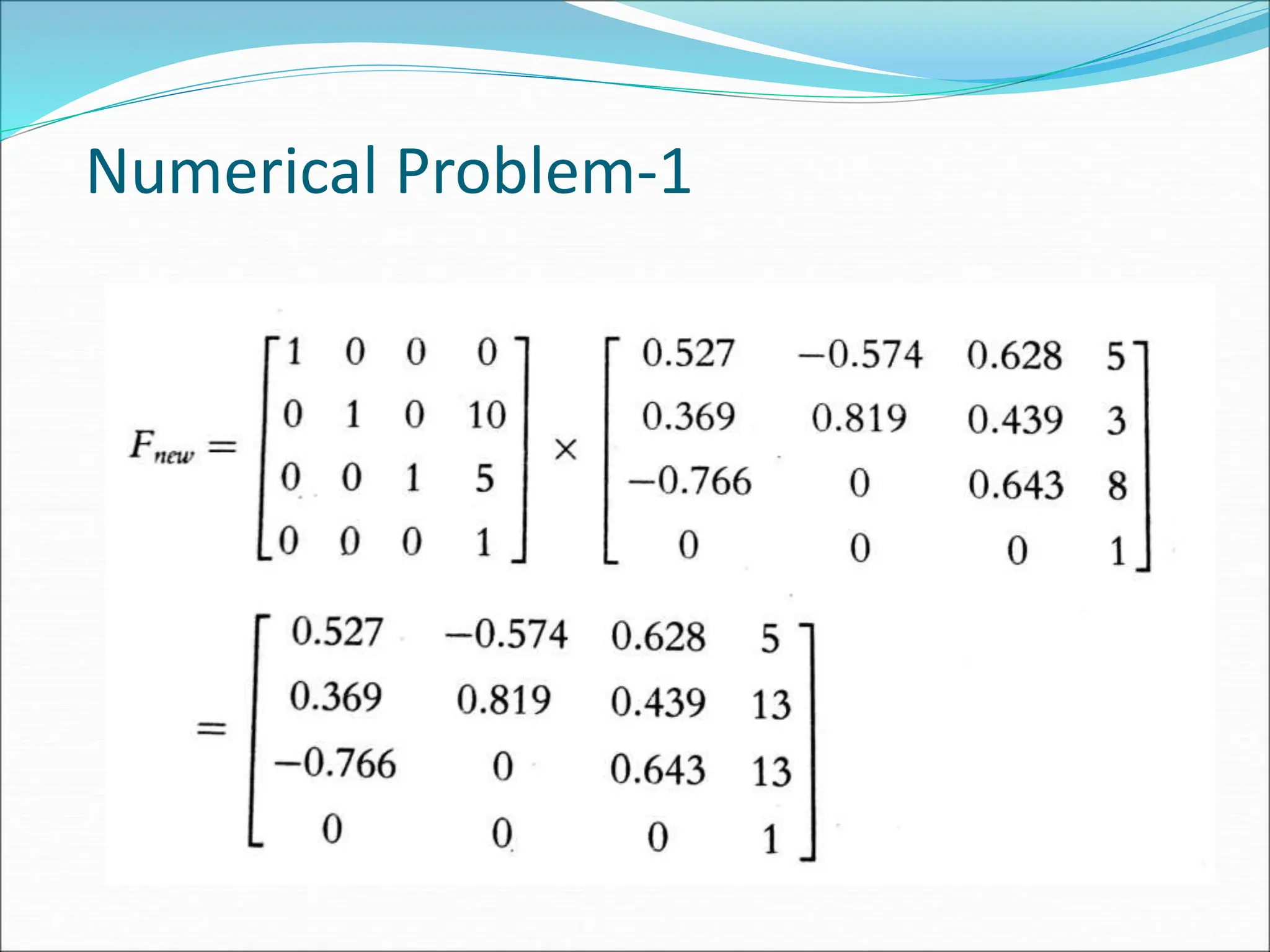
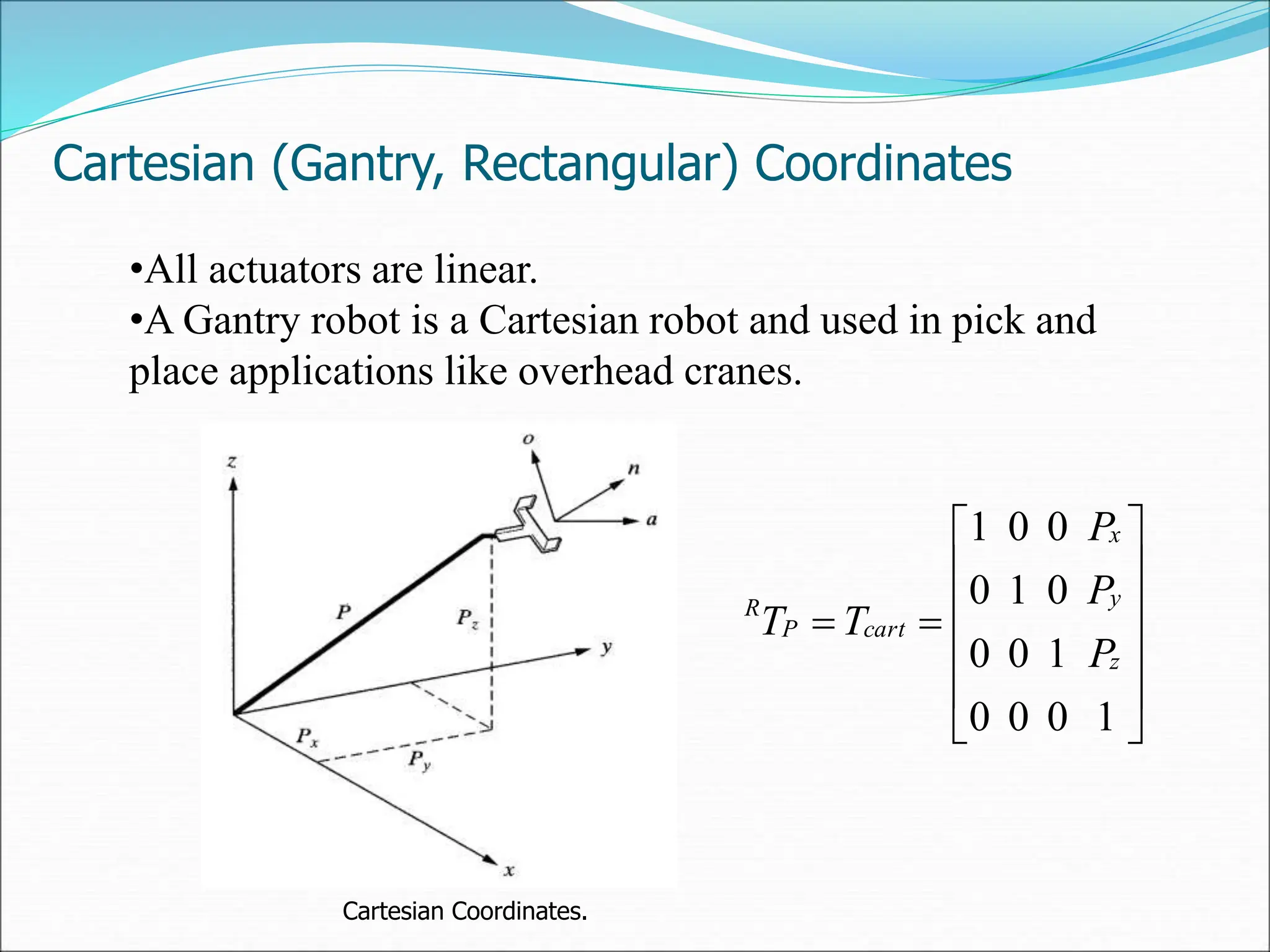
The document provides a detailed overview of robot kinematics, including forward and inverse kinematics for determining robot hand positions and joint variables. It covers matrix representations for points, vectors, and transformations in space, alongside numerical problems illustrating these concepts. Additionally, various robot coordinate systems, such as Cartesian, cylindrical, and spherical coordinates, are discussed for position analysis.

1. Content
 Introduction
 Matrix Representation
 Transformations
 Standard Robot coordinate System
 Numericals

2. Robot Kinematics: Position Analysis
INTRODUCTION
Forward Kinematics:
to determine where the robot’s hand is?
(If all joint variables are known)
Inverse Kinematics:
to calculate what each joint variable is?
(If we desire that the hand be
located at a particular point)

3. Matrix Representation
- Representation Of A Point In Space
Representation of a point in space
A point P in space :
3 coordinates relative to a reference frame
^
^
^
k
c
j
b
i
a
P z
y
x 



4. Representation of a vector in space
A Vector P in space :
3 coordinates of its tail and of its head
^
^
^
__
k
c
j
b
i
a
P z
y
x 















w
z
y
x
P
__
Matrix Representation
-Representation of a Vector in Space
Where is Scale
factor
w

5.  It can Change overall size of vector similar to
zooming function in computer graphics.
 When w=1 ,
 Size of components remain unchanged
 When w=0,
 It represent a vector whose length is infinite but it
represents the direction so called as directional
vector
Scale Factor w

6. Representation of a frame at the origin of the reference frame
Each Unit Vector is mutually perpendicular. :
normal, orientation, approach vector











z
z
z
y
y
y
x
x
x
a
o
n
a
o
n
a
o
n
F
Matrix Representation
-Representation of a Frame at the Origin of a Fixed-
Reference Frame

7. Representation of a frame in a frame
Each Unit Vector is mutually perpendicular. :
normal, orientation, approach vector













1
0
0
0
z
z
z
z
y
y
y
y
x
x
x
x
P
a
o
n
P
a
o
n
P
a
o
n
F
Representation of a Frame in a Fixed Reference
Frame

8. Representation of an object in space
An object can be represented in space by attaching a frame
to it and representing the frame in space.













1
0
0
0
z
z
z
z
y
y
y
y
x
x
x
x
object
P
a
o
n
P
a
o
n
P
a
o
n
F
Representation of a Rigid Body

9. Homogeneous Transformation Matrices
A transformation matrices must be in square form.
• It is much easier to calculate the inverse of square matrices.
• To multiply two matrices, their dimensions must match.













1
0
0
0
z
z
z
z
y
y
y
y
x
x
x
x
P
a
o
n
P
a
o
n
P
a
o
n
F

10. Transformations
 A transformation is defined as making a movement
in space.
 Types of Transformation are:
 A pure translation
 A pure rotation
 A combination of translation and rotation

11. Representation of a Pure Translation
Representation of an pure translation in space













1
0
0
0
1
0
0
0
1
0
0
0
1
z
y
x
d
d
d
T
 If a frame moves in space without any change in its
orientation

12. Numerical Problem-1
A frame F has been moved 10 units along y-axis and 5 units
along z-axis of reference frame. Find new location of
frame.
Answer:

13. Numerical Problem-1

14. Pure Rotation about an Axis
Coordinates of a point in a rotating frame before and after rotation.
Assumption : The frame is at the origin of the reference
frame and parallel to it.

15. Pure Rotation about an Axis

16. Combined Transformations
 Combined Transformation consist of a number of
successive translations and rotations about fixed
reference frame axes.
 The order of matrices written is the opposite of the
order of transformations performed.
 If order of matrices changes then final position of
robot also changes

17. Numerical Problem (Forward Kinematics)-2
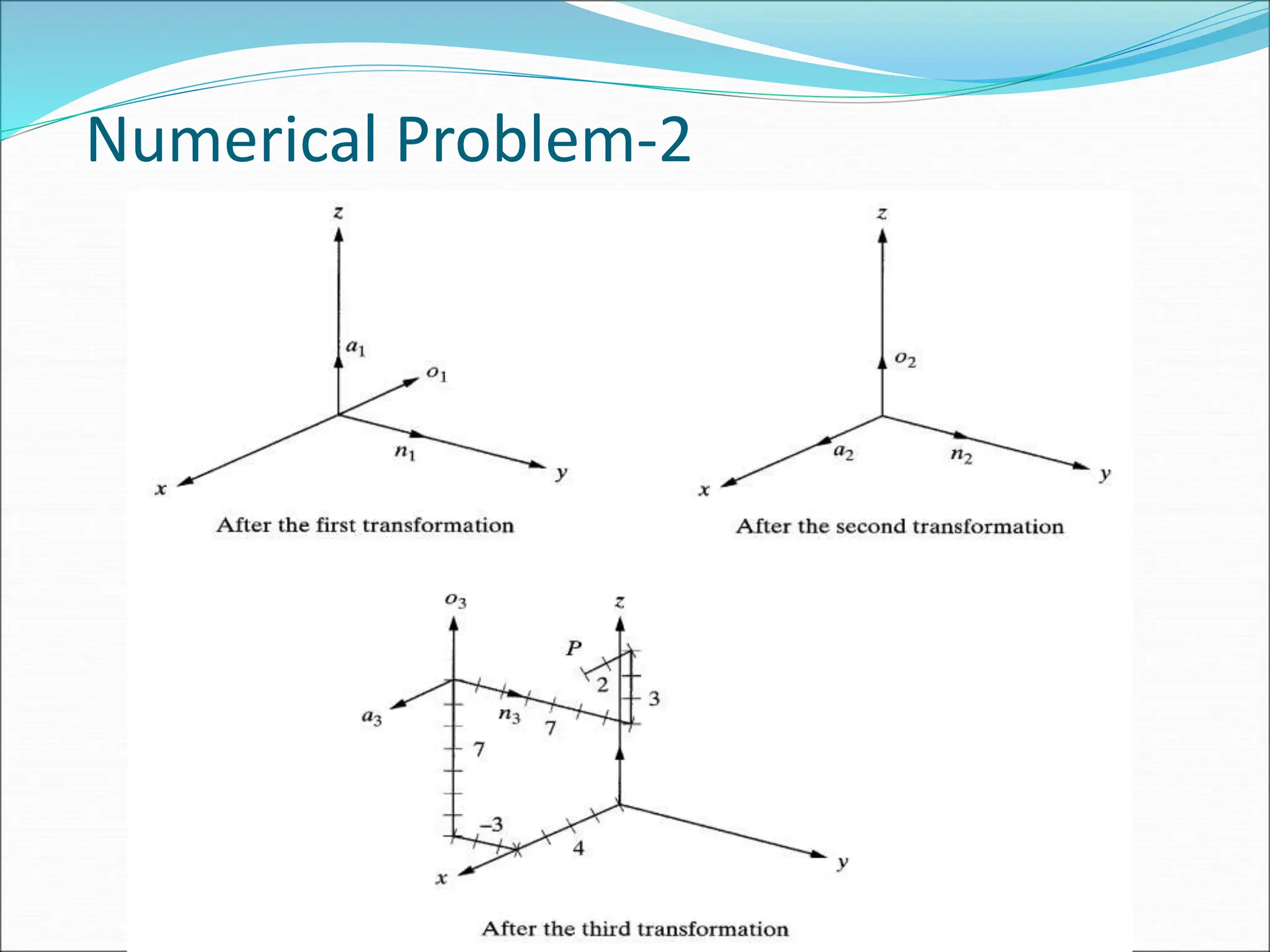
A point p(7,3,1) is attached to frame and subjected to
following transformations. Find coordinate of point
relative to reference frame.
1. Rotation of 90° about z-axis
2. Followed by rotation of 90 about y-axis
3. Followed by translation of [4,-3,7].
Answer: The matrix equation is given as

18. Numerical Problem-2

19. Fig. 2.13 Effects of three successive transformations
A number of successive translations and rotations….
Numerical Problem-2

20. Forward Kinematics and Inverse Kinematics equation
for position analysis and three types of standard robot
coordinate system are:
(a) Cartesian (gantry, rectangular) coordinates.
(b) Cylindrical coordinates.
(c) Spherical coordinates.
Forward and Inverse Kinematics Equations for Position

21. Cartesian (Gantry, Rectangular) Coordinates
•All actuators are linear.
•A Gantry robot is a Cartesian robot and used in pick and
place applications like overhead cranes.
Cartesian Coordinates.














1
0
0
0
1
0
0
0
1
0
0
0
1
z
y
x
cart
P
R
P
P
P
T
T

22. Cylindrical Coordinates
• 2 Linear translations and 1 rotation
• translation of r along the x-axis
• rotation of  about the z-axis
• translation of l along the z-axis











 


1
0
0
0
1
0
0
0
0
l
rS
C
S
rC
S
C
T
T cyl
P
R 





,0,0)
)Trans(
,
)Rot(
Trans(0,0,
)
,
,
( r
z
l
l
r
T
T cyl
P
R

 


23. Suppose we desire to place the origin of hand frame of a
cylindrical robot at [ 3,4,7]. Calculate the joint variables of
robot.
Answer:
Numerical Problem (Inverse Kinematics)-3











 


1
0
0
0
1
0
0
0
0
l
rS
C
S
rC
S
C
T
T cyl
P
R 




 r= 5 units

24. Spherical Coordinates
• 2 Linear translations and 1 rotation
• translation of r along the z-axis
• rotation of  about the y-axis
• rotation of  along the z-axis
Spherical Coordinates.






















1
0
0
0
0 
















rC
C
S
S
rS
S
S
C
S
C
C
rS
C
S
S
C
C
T
T sph
P
R
)
)Trans(
)Rot(
Rot(
)
( 0,0,
,
,
,
, 


 y
z
l
r
sph
P
R
T
T 
