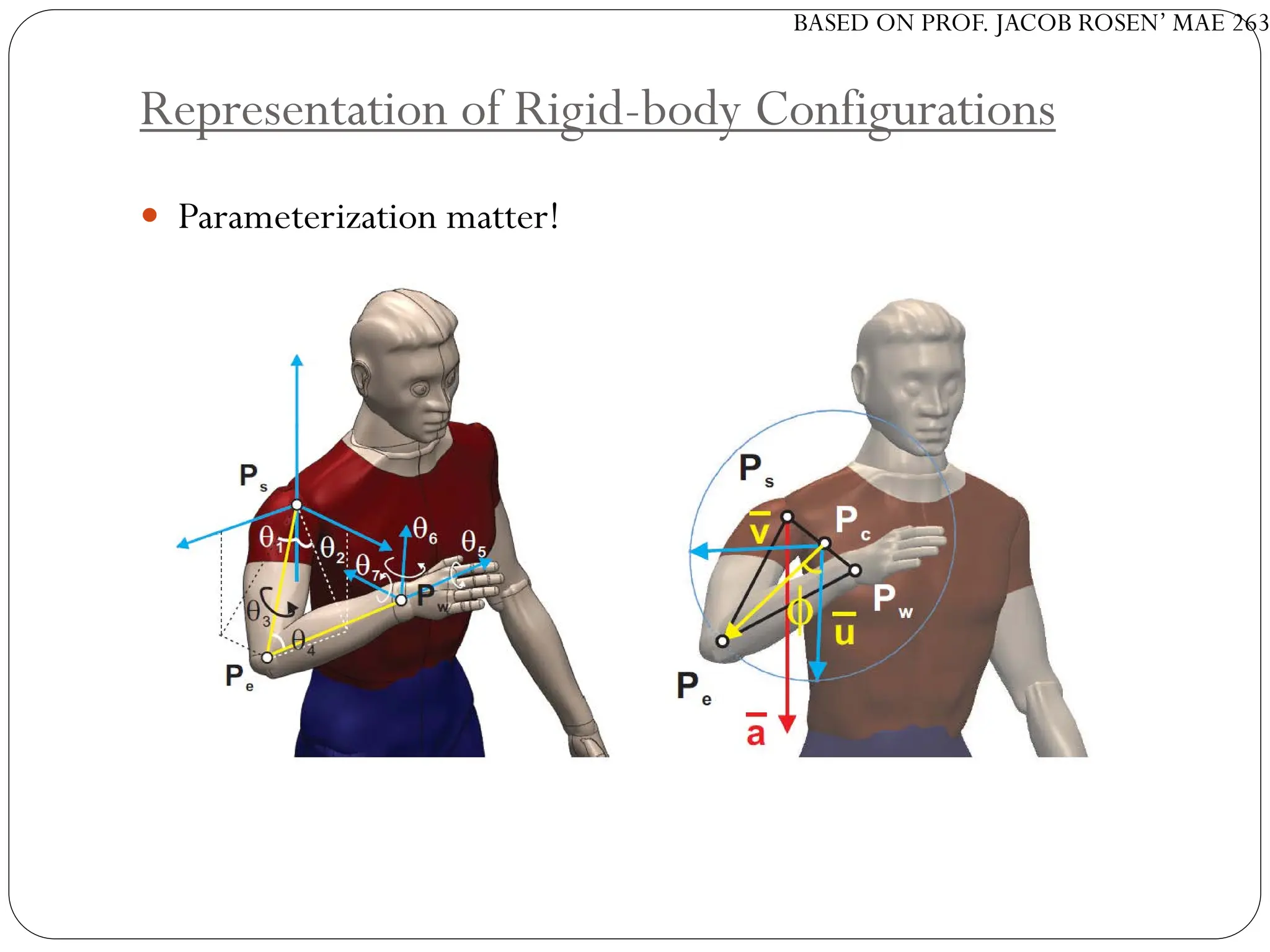
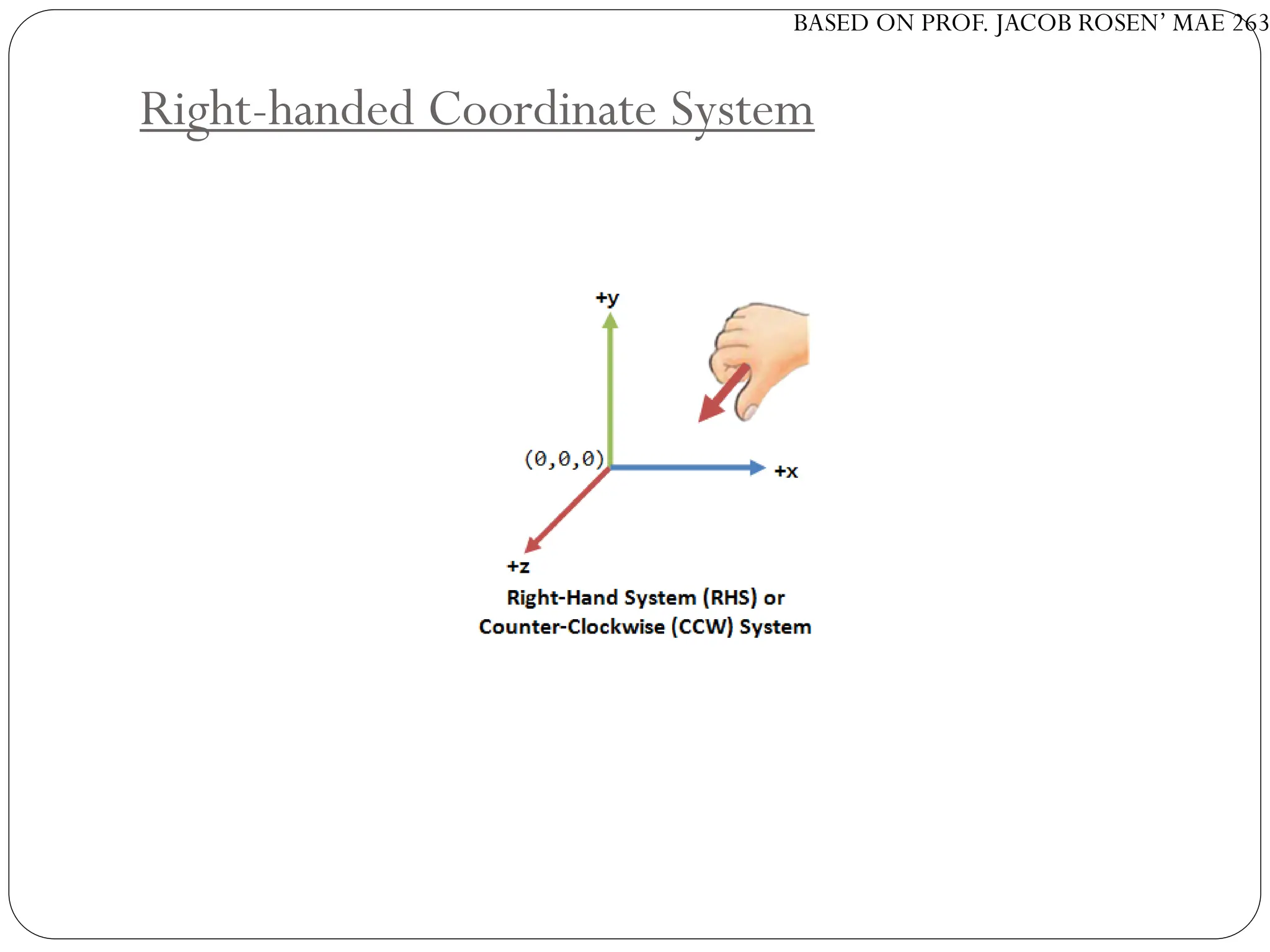
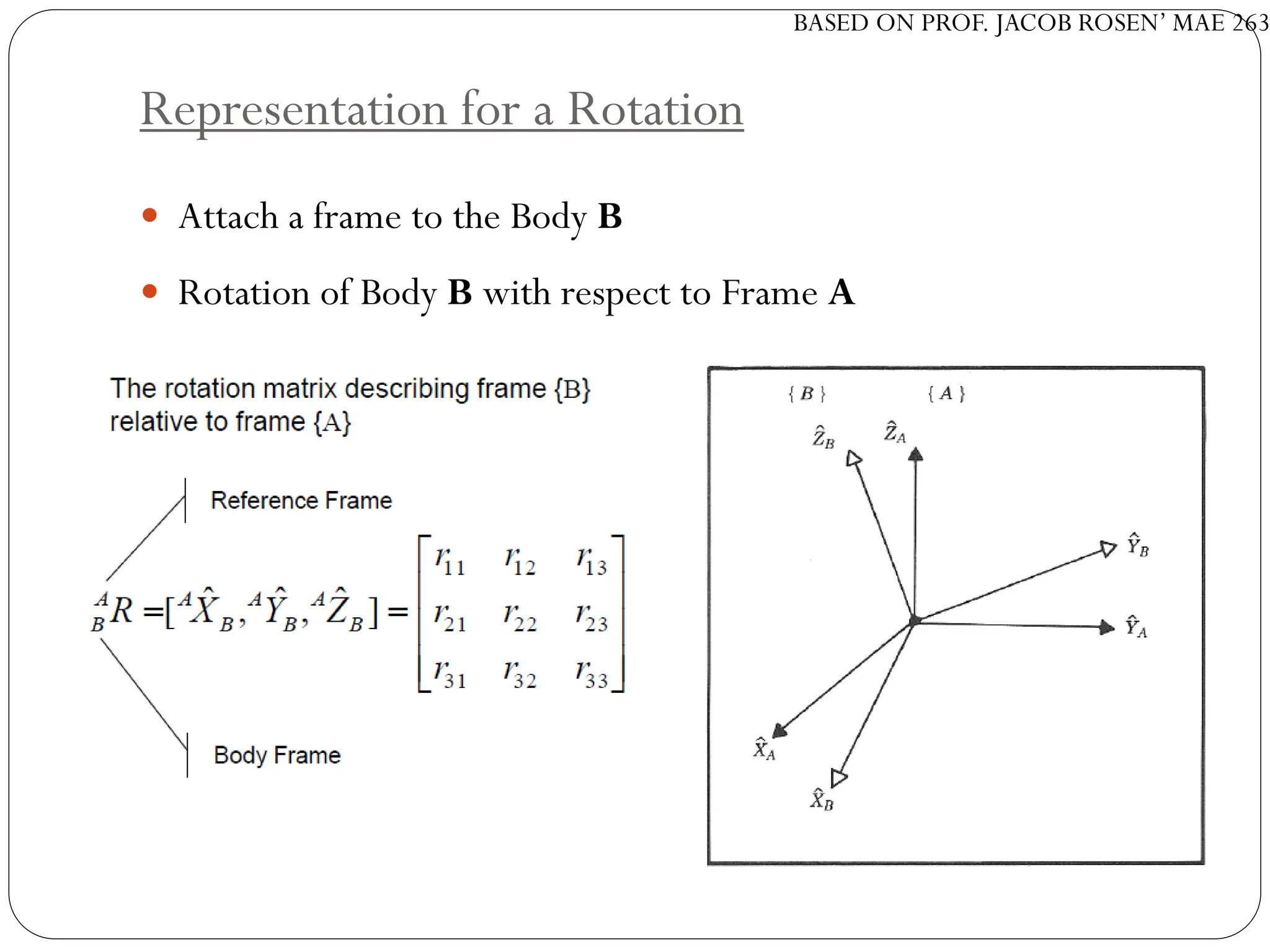
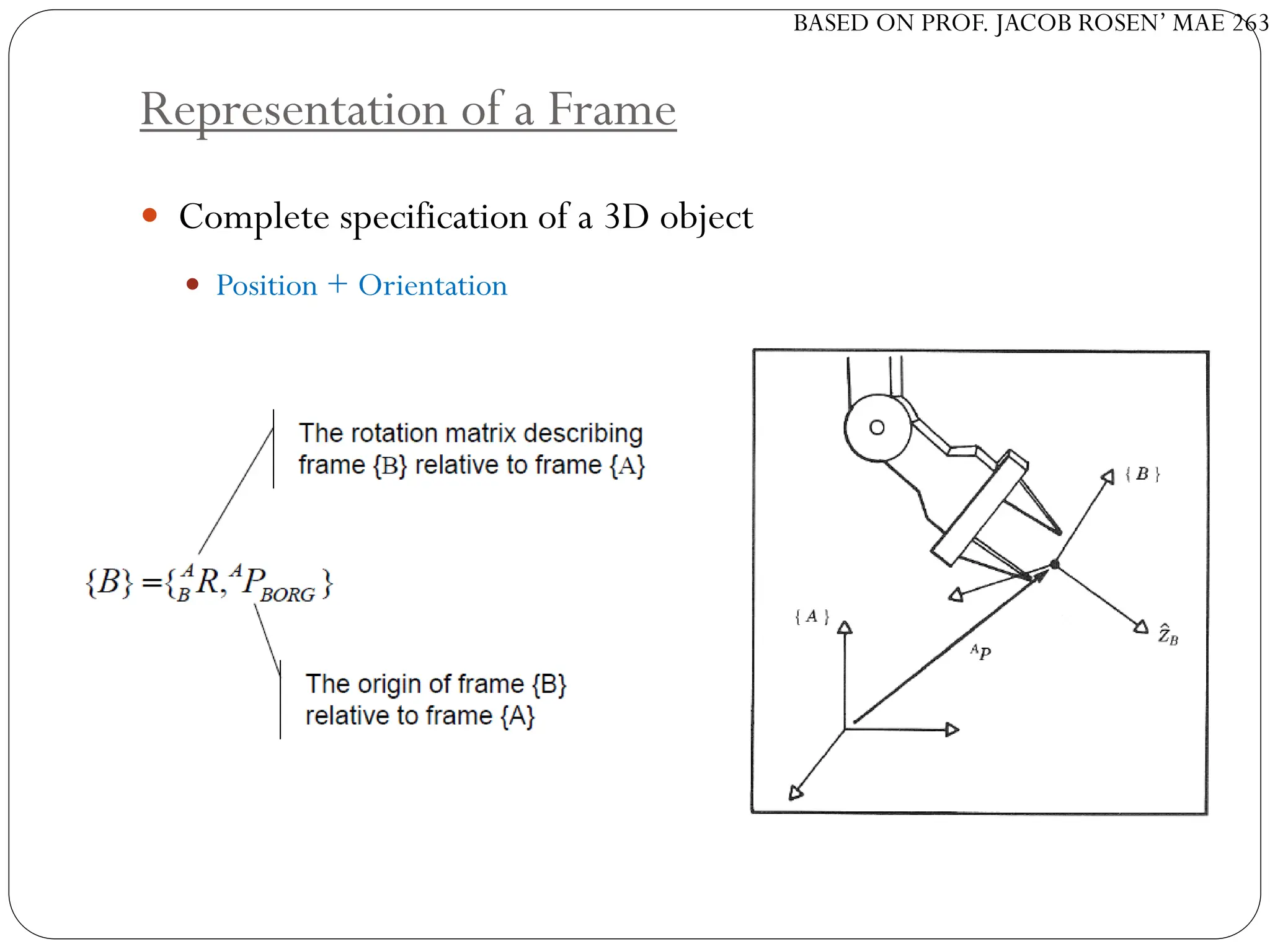
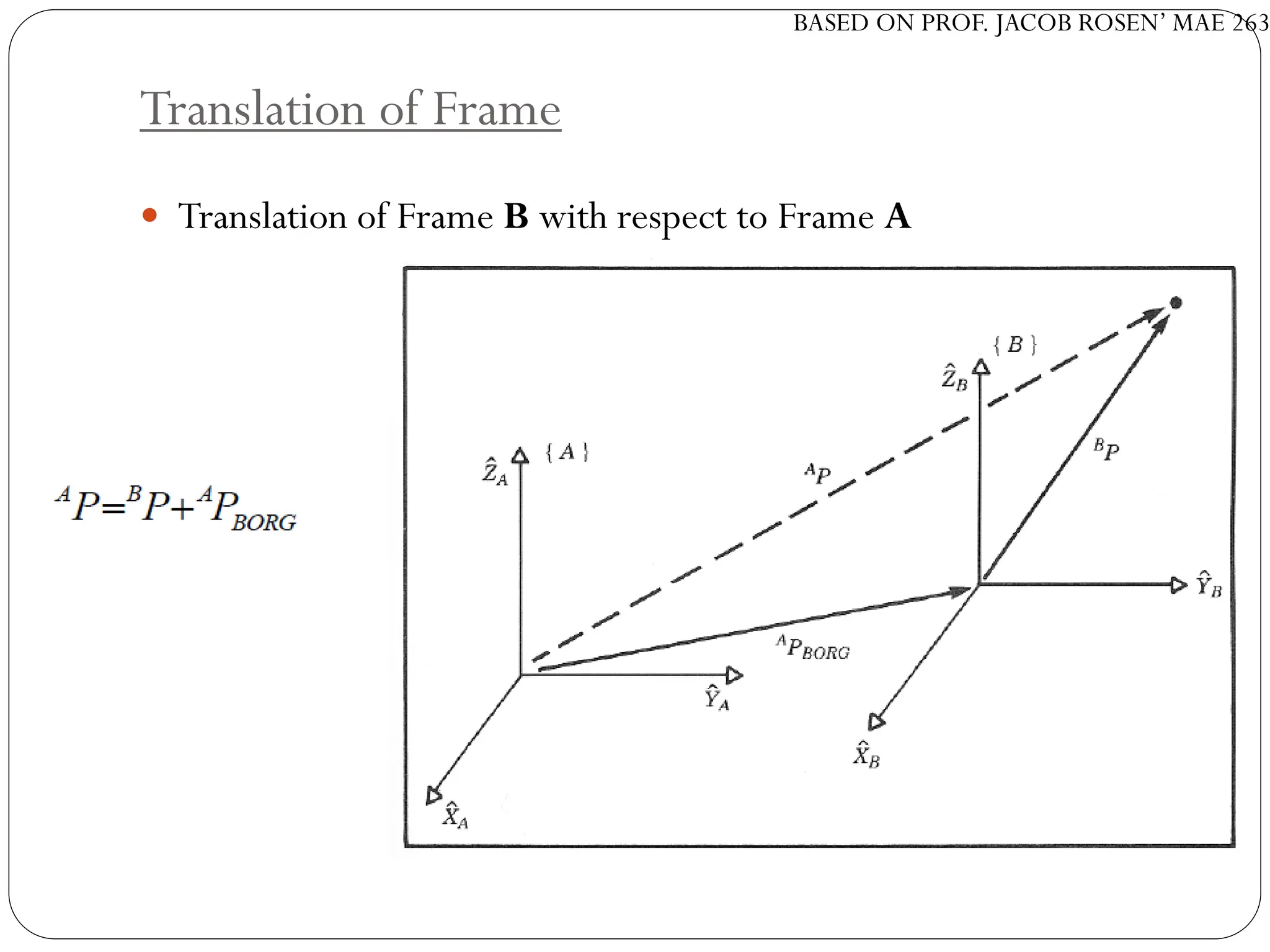
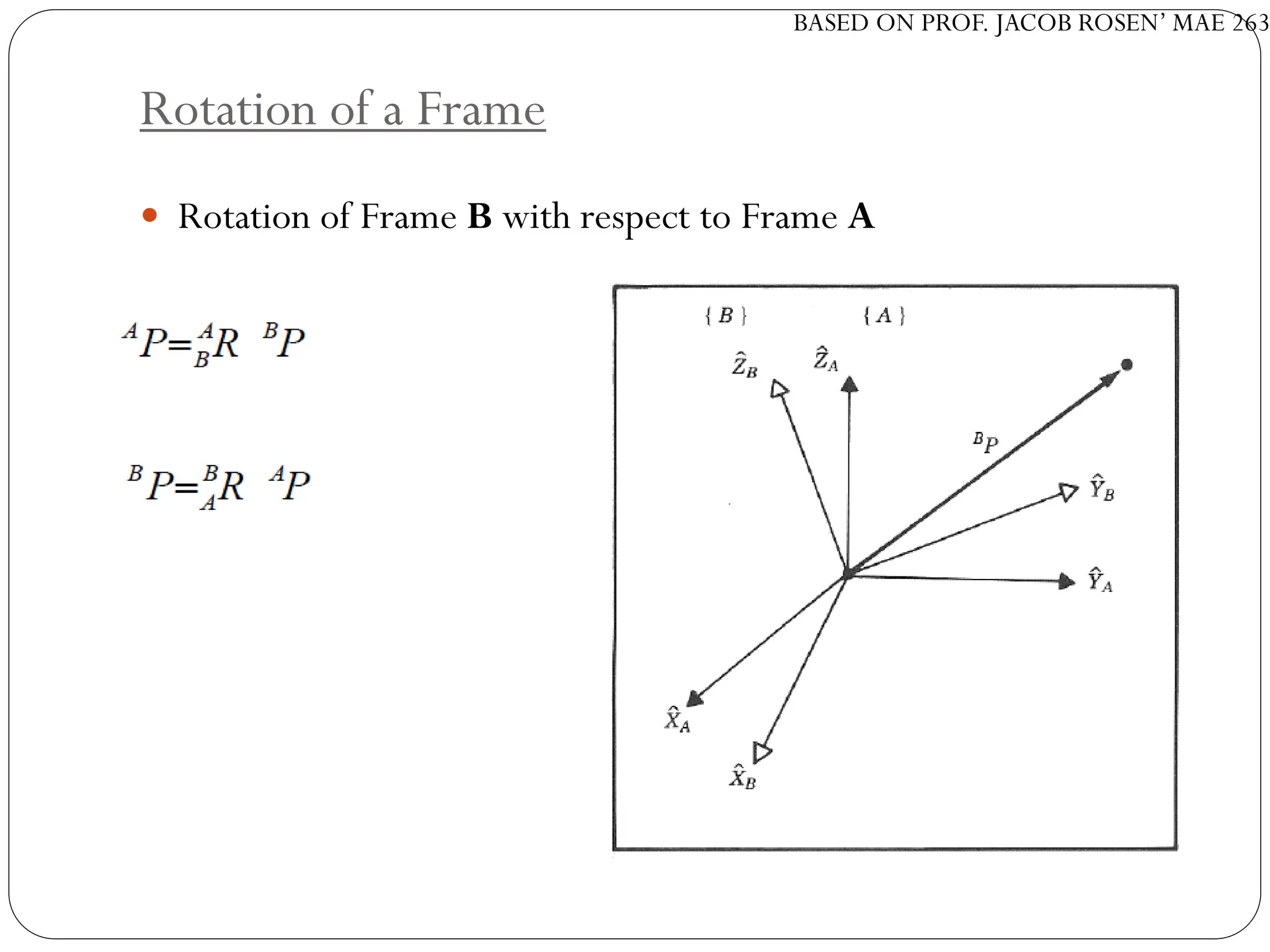
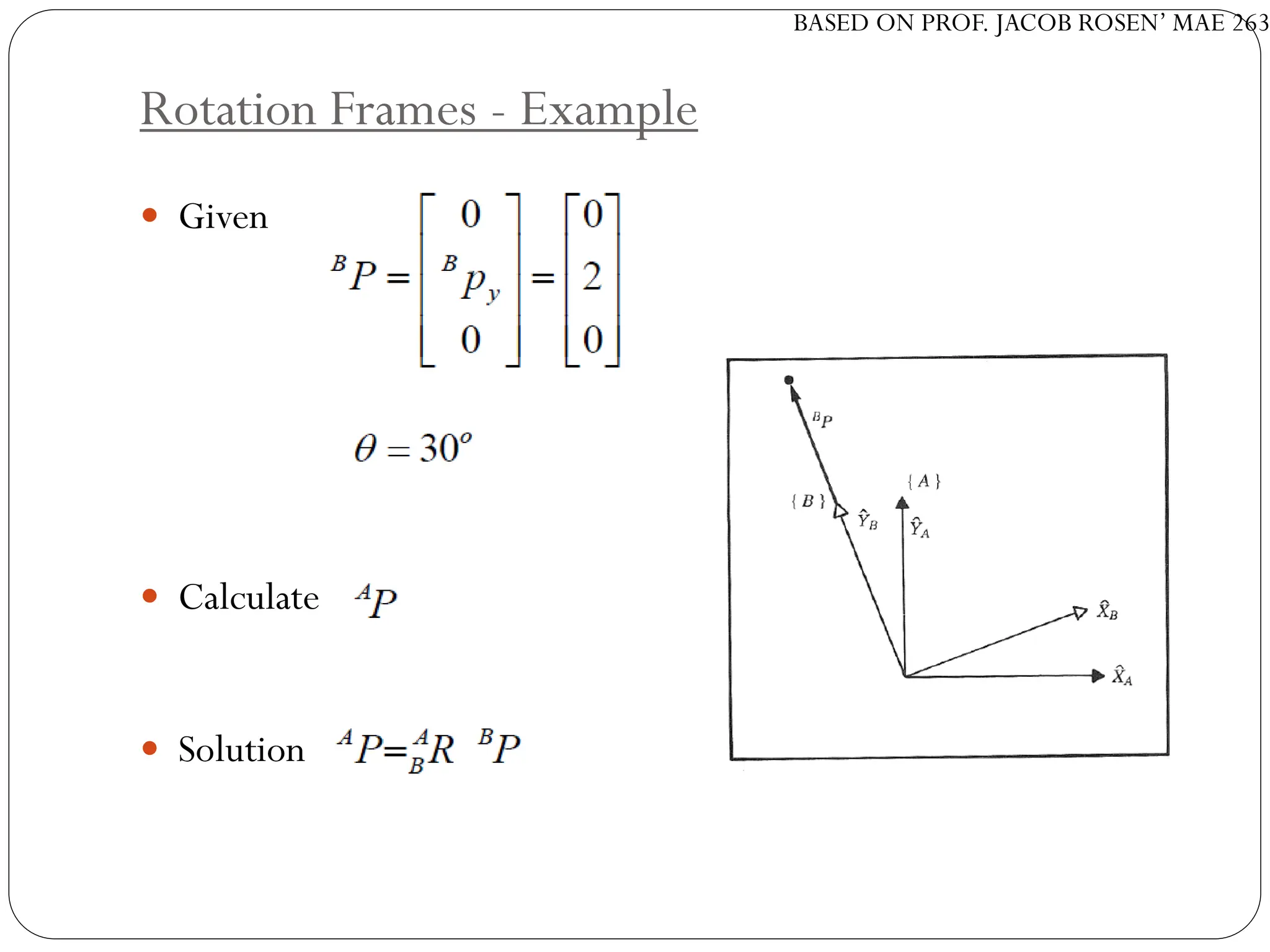
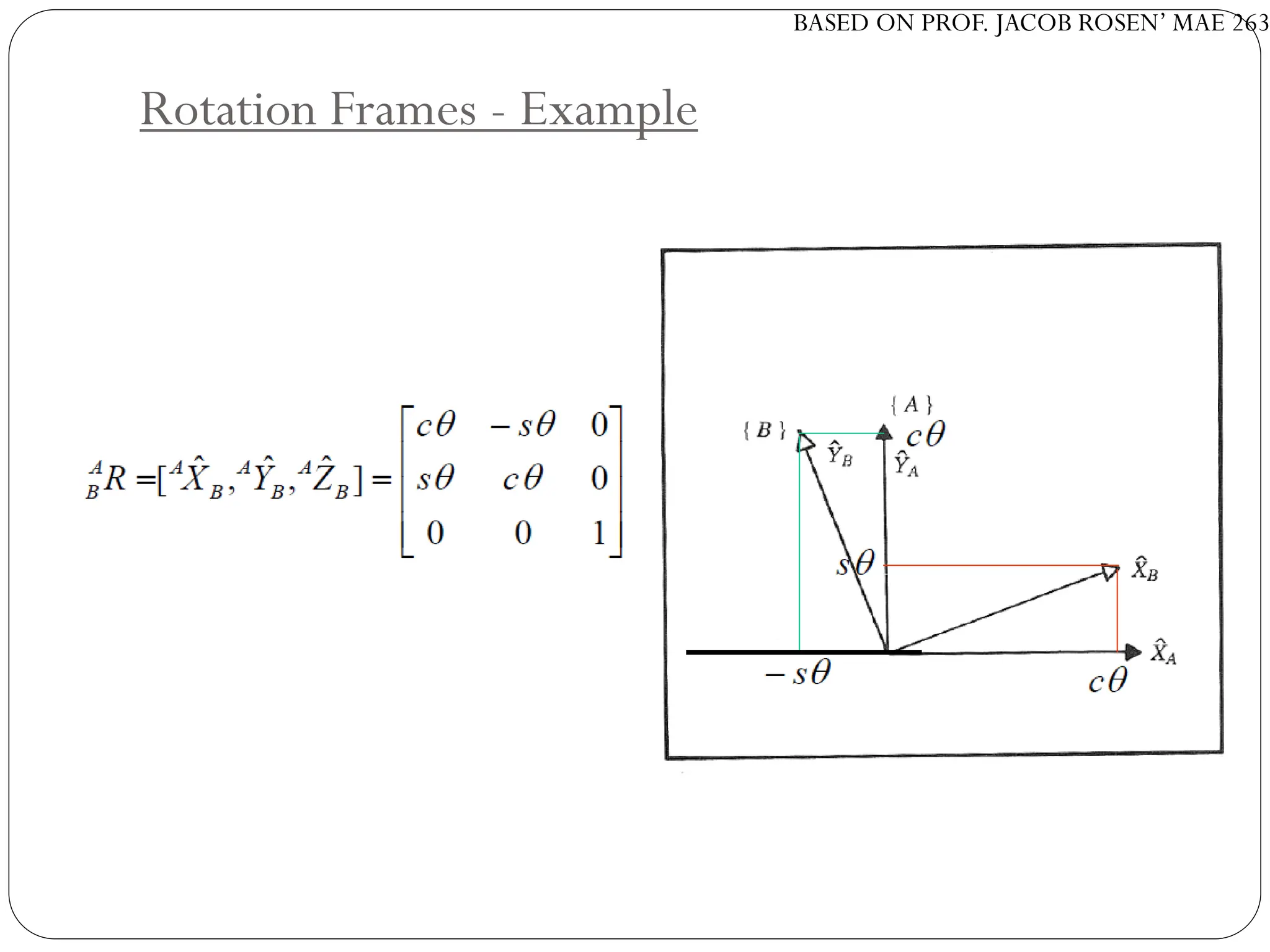
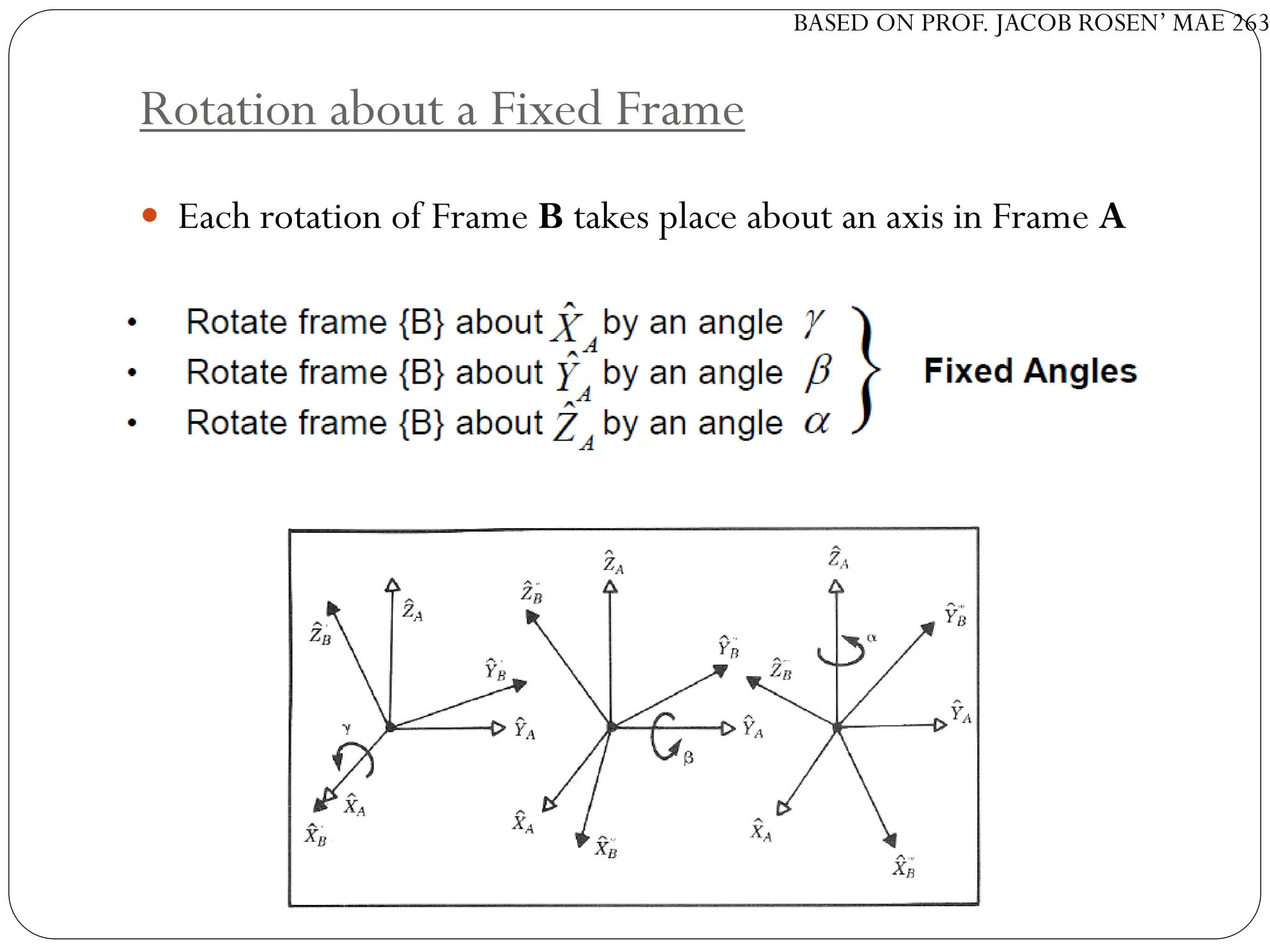
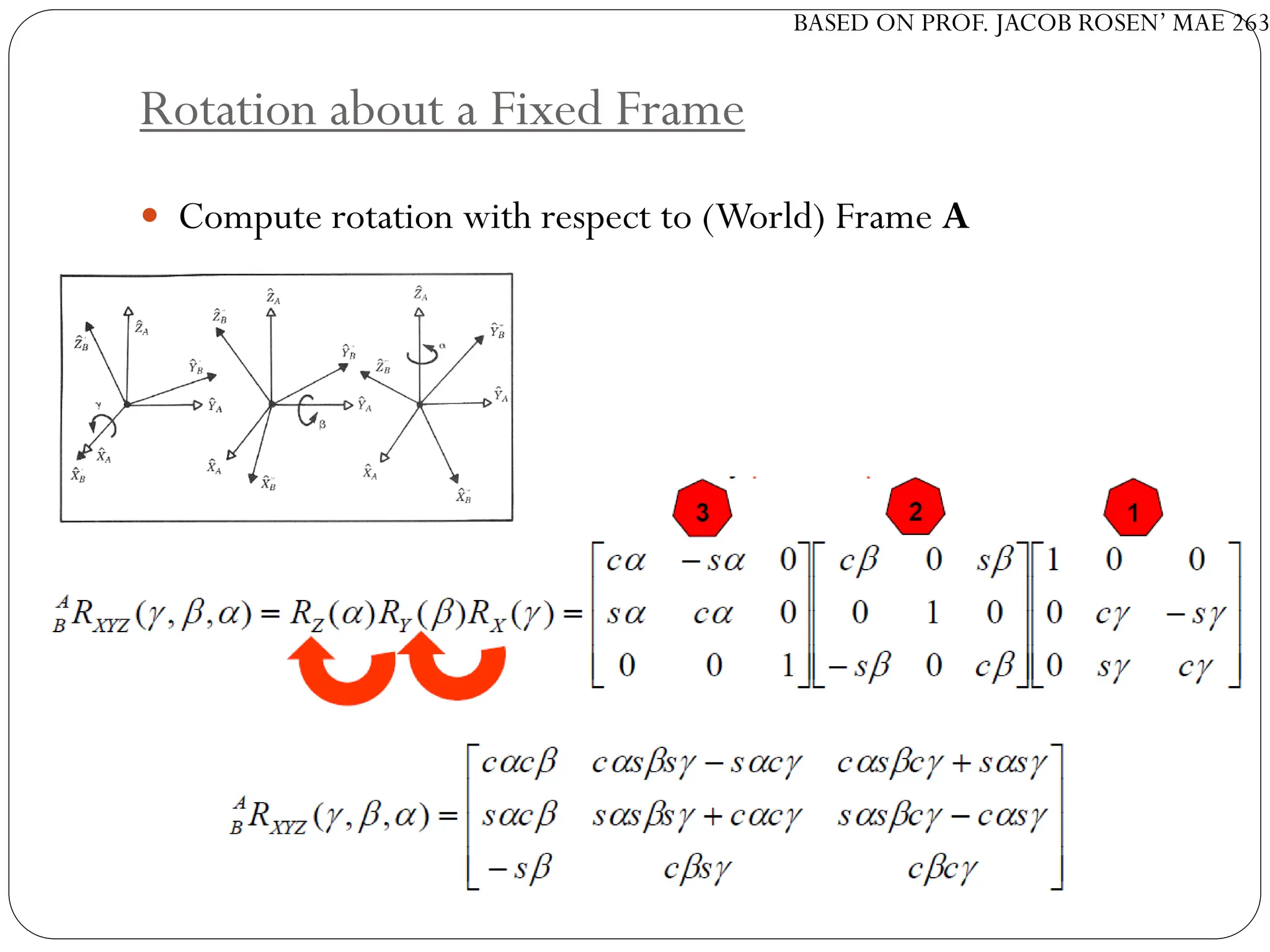
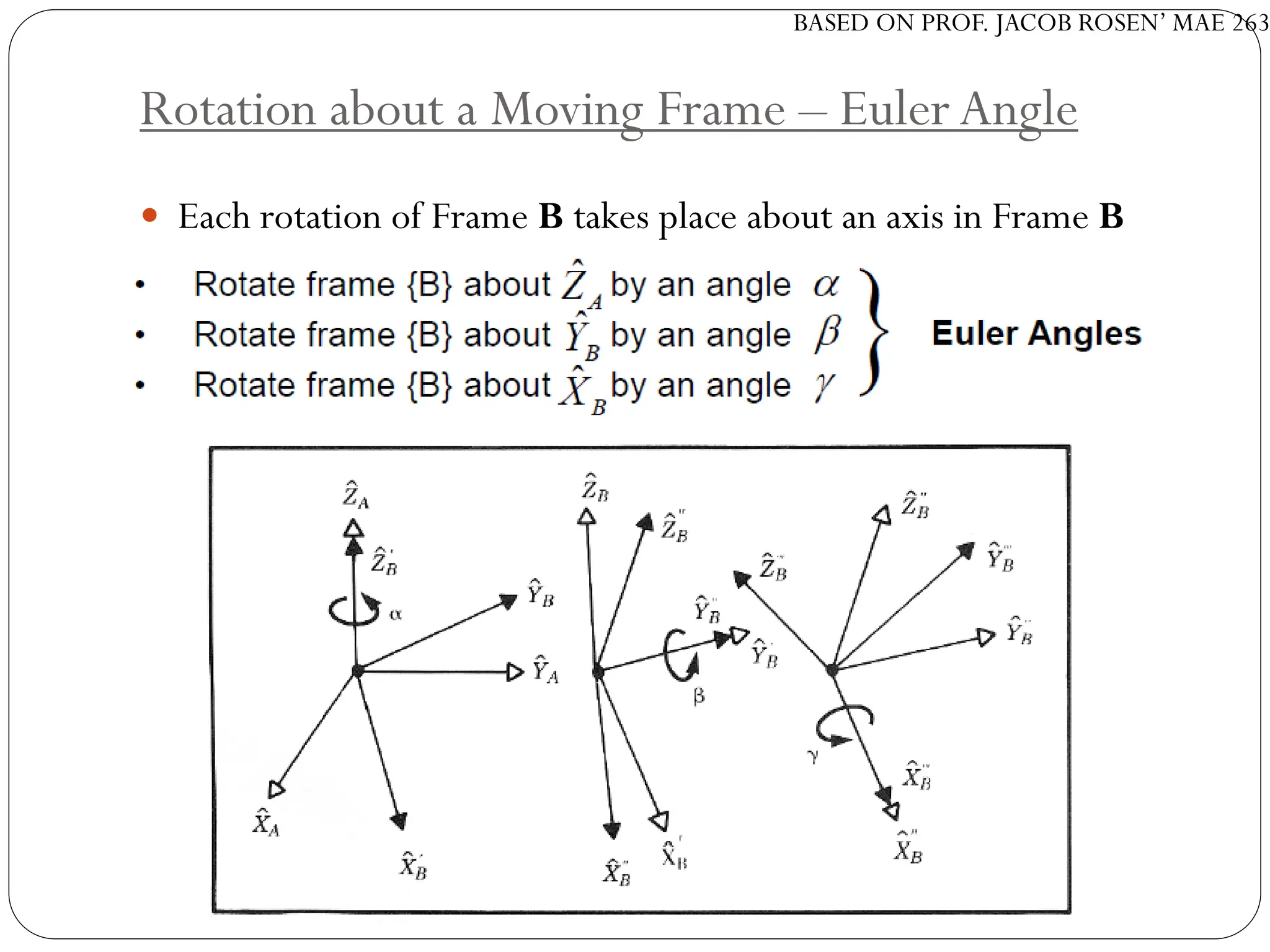
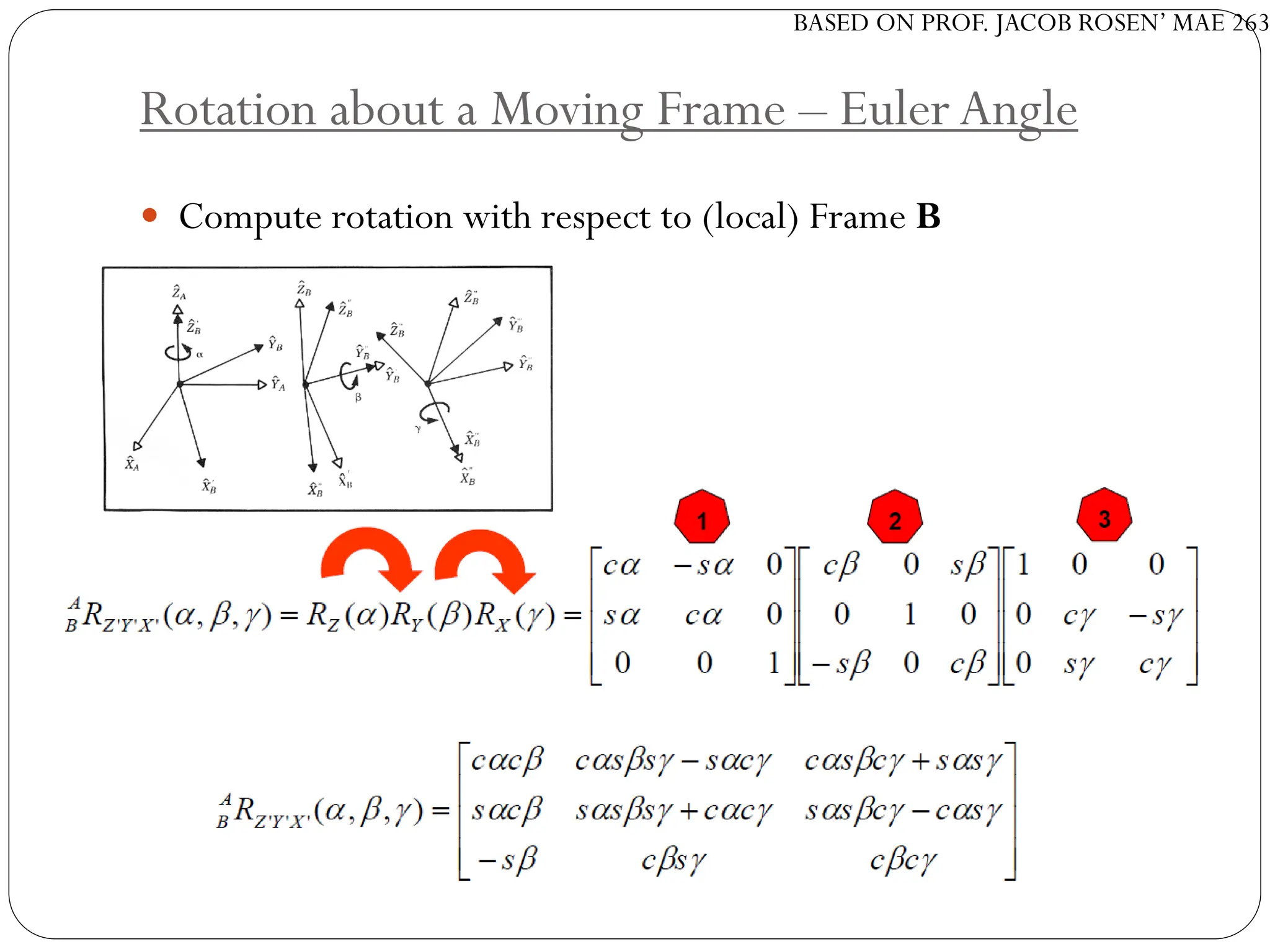
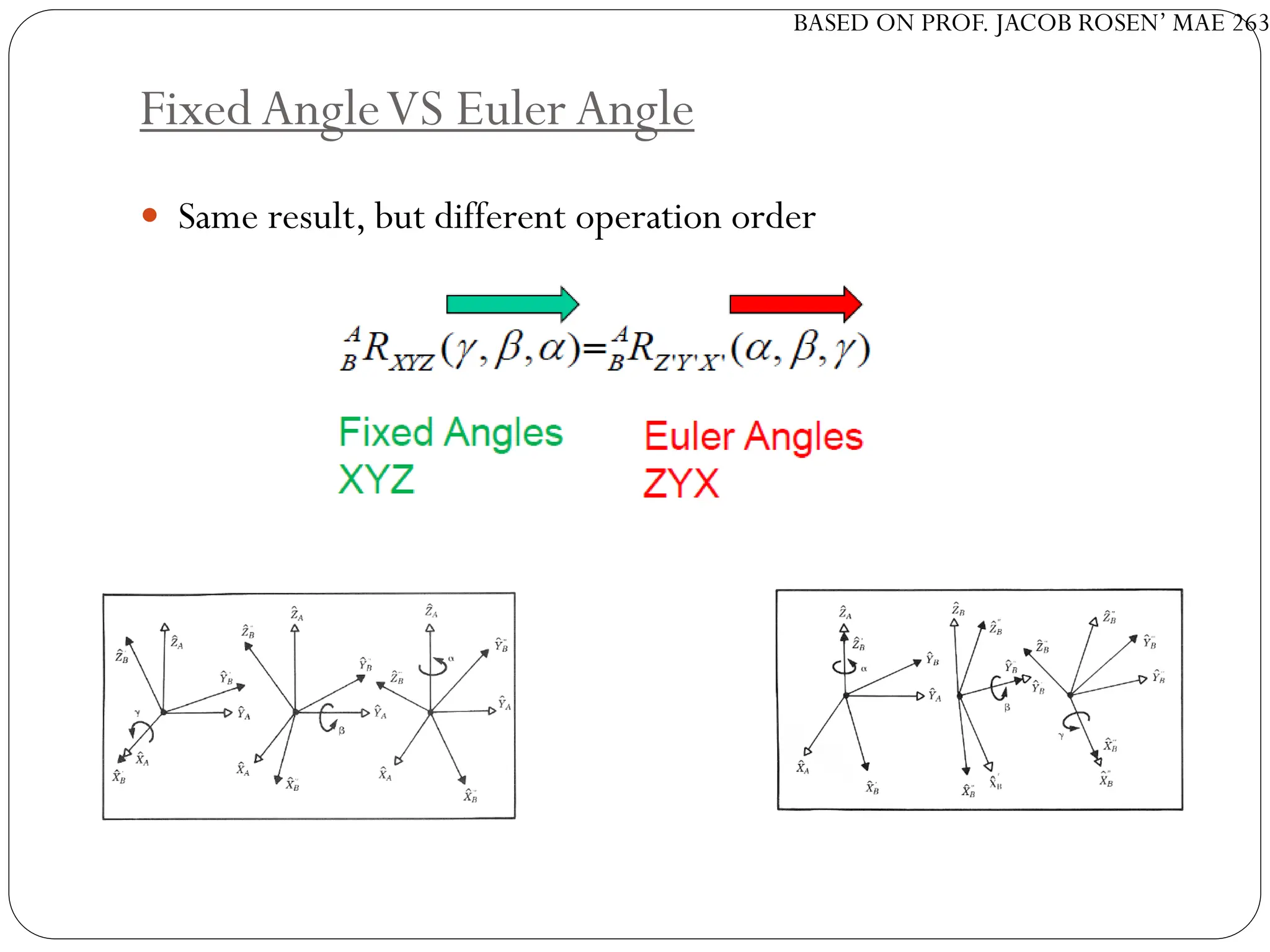
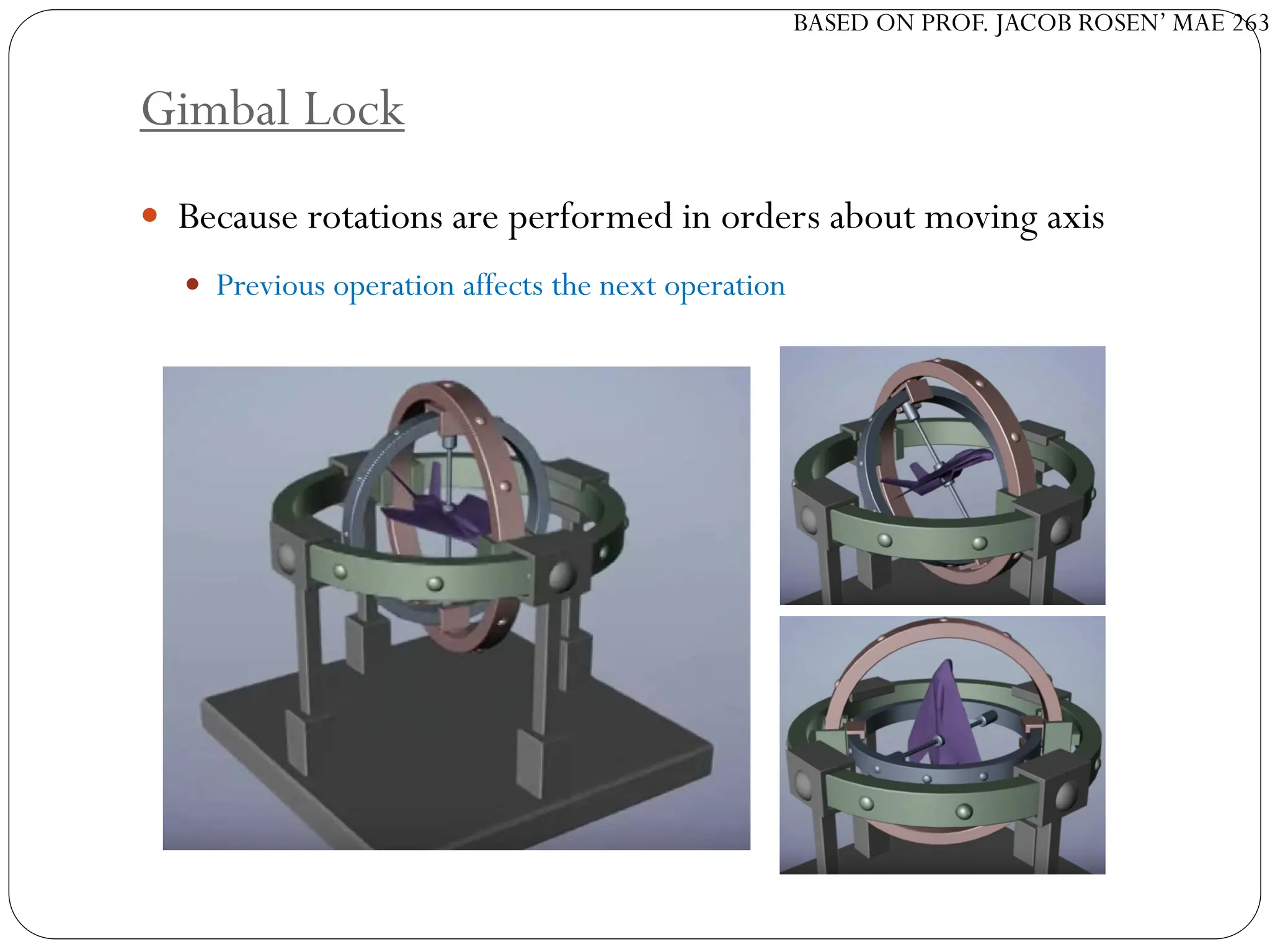
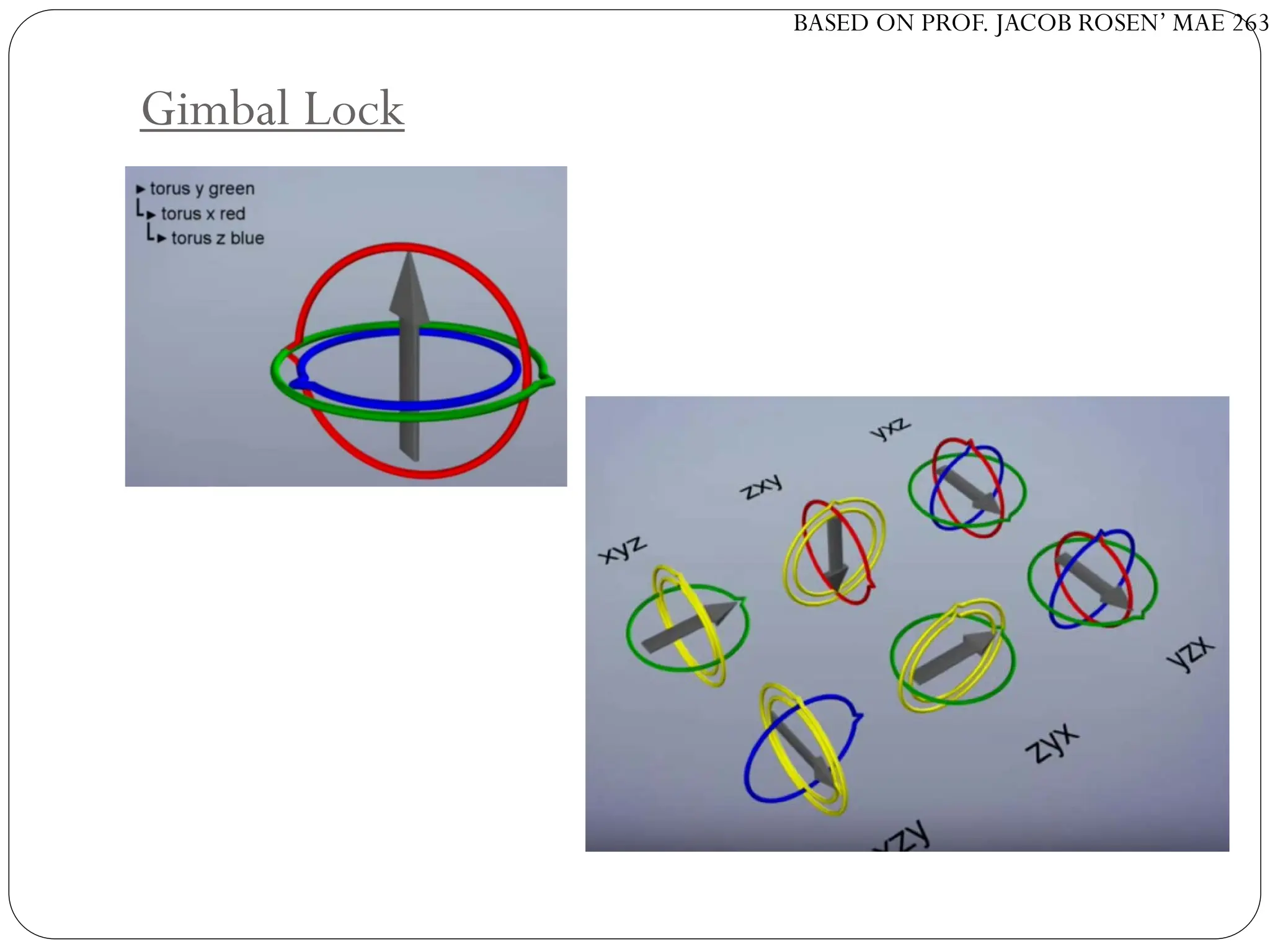
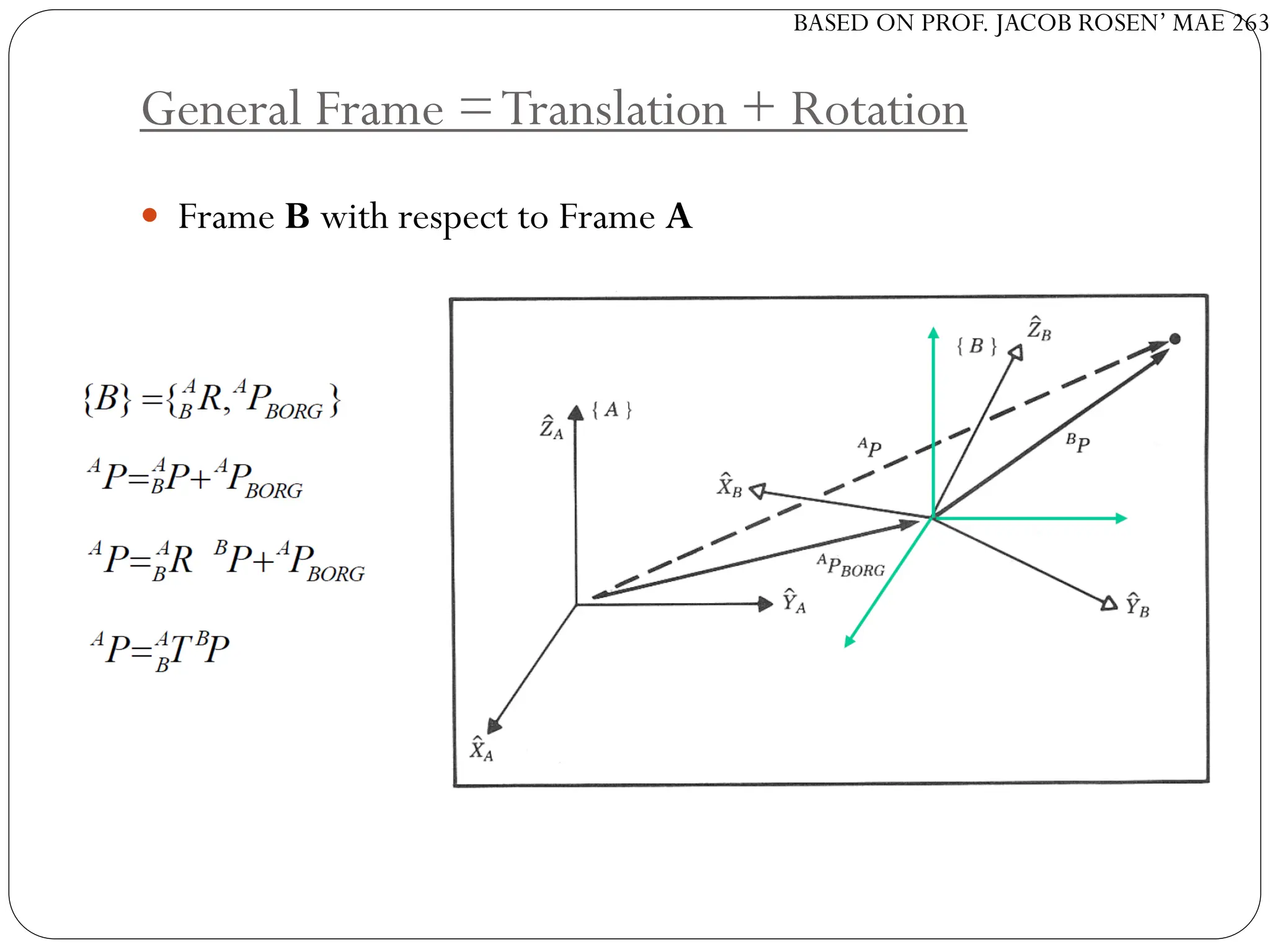
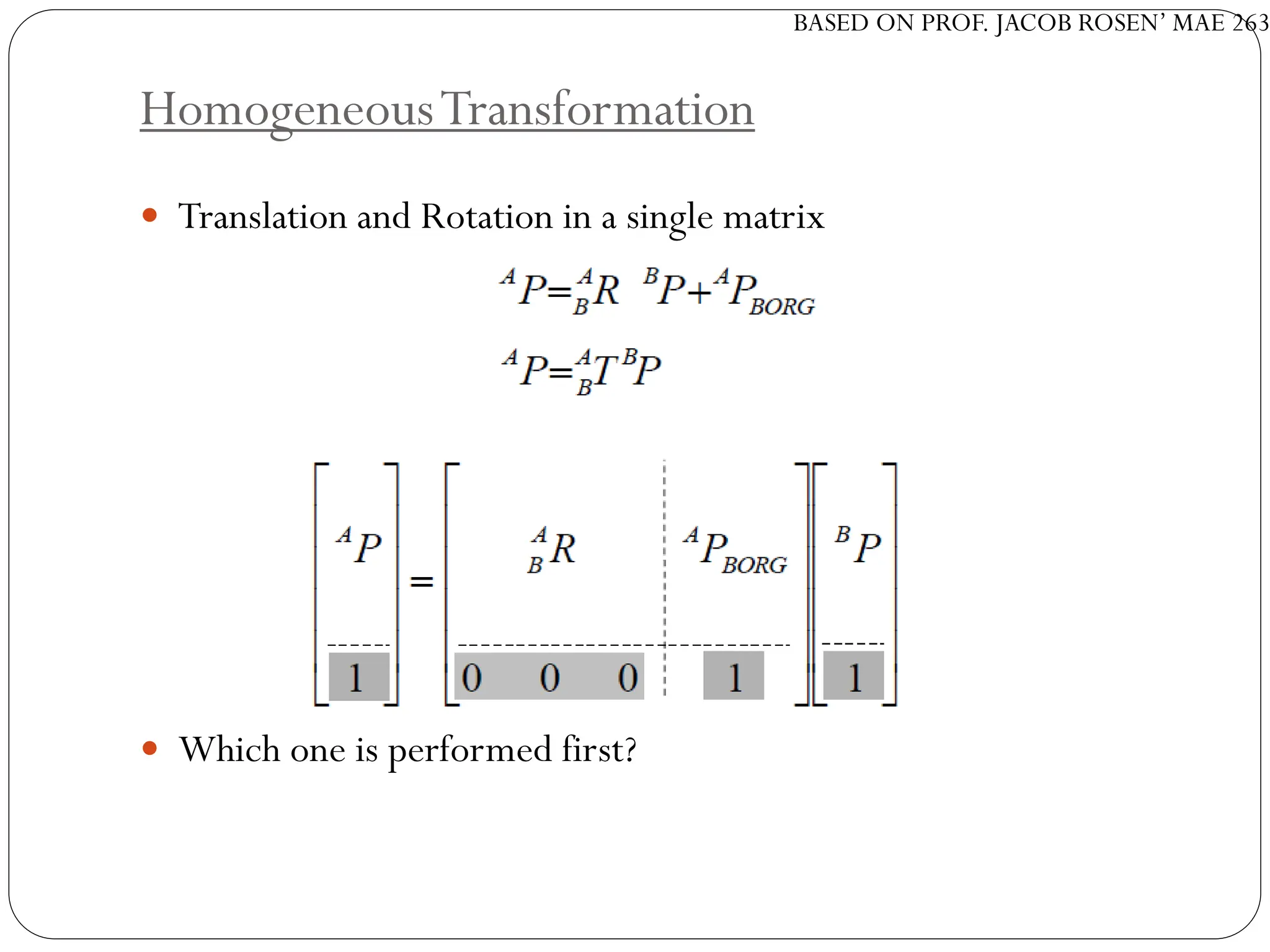
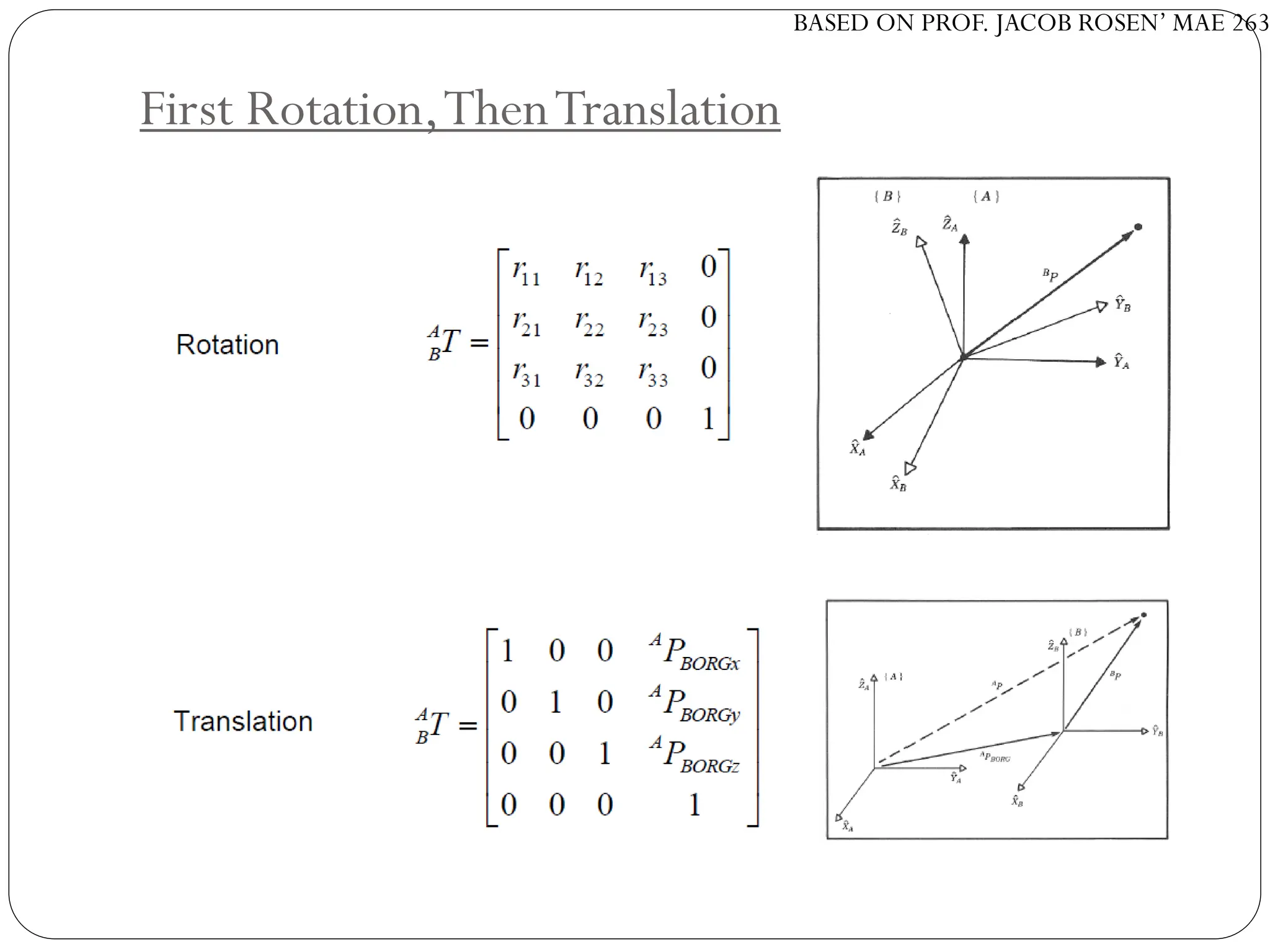
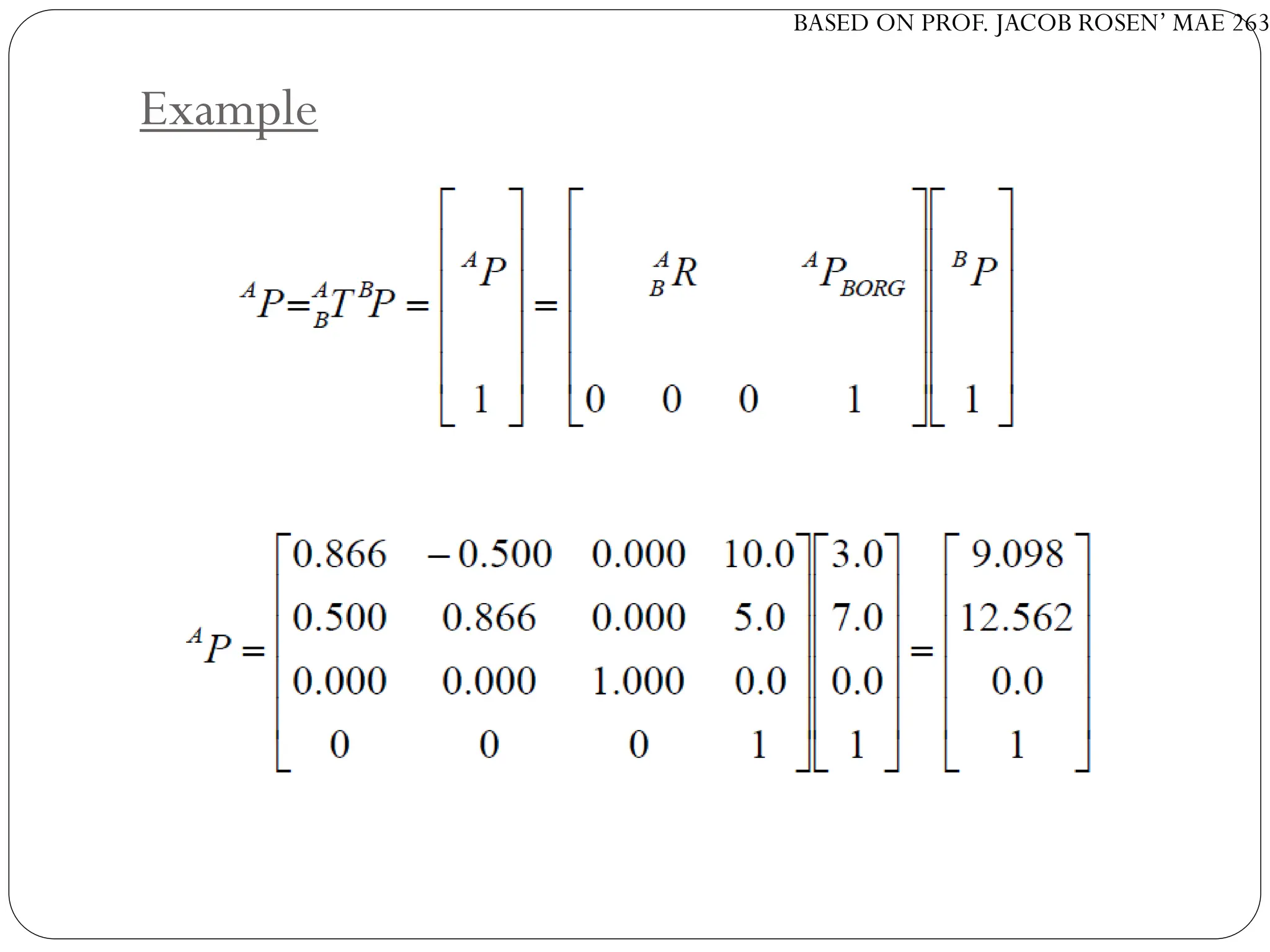
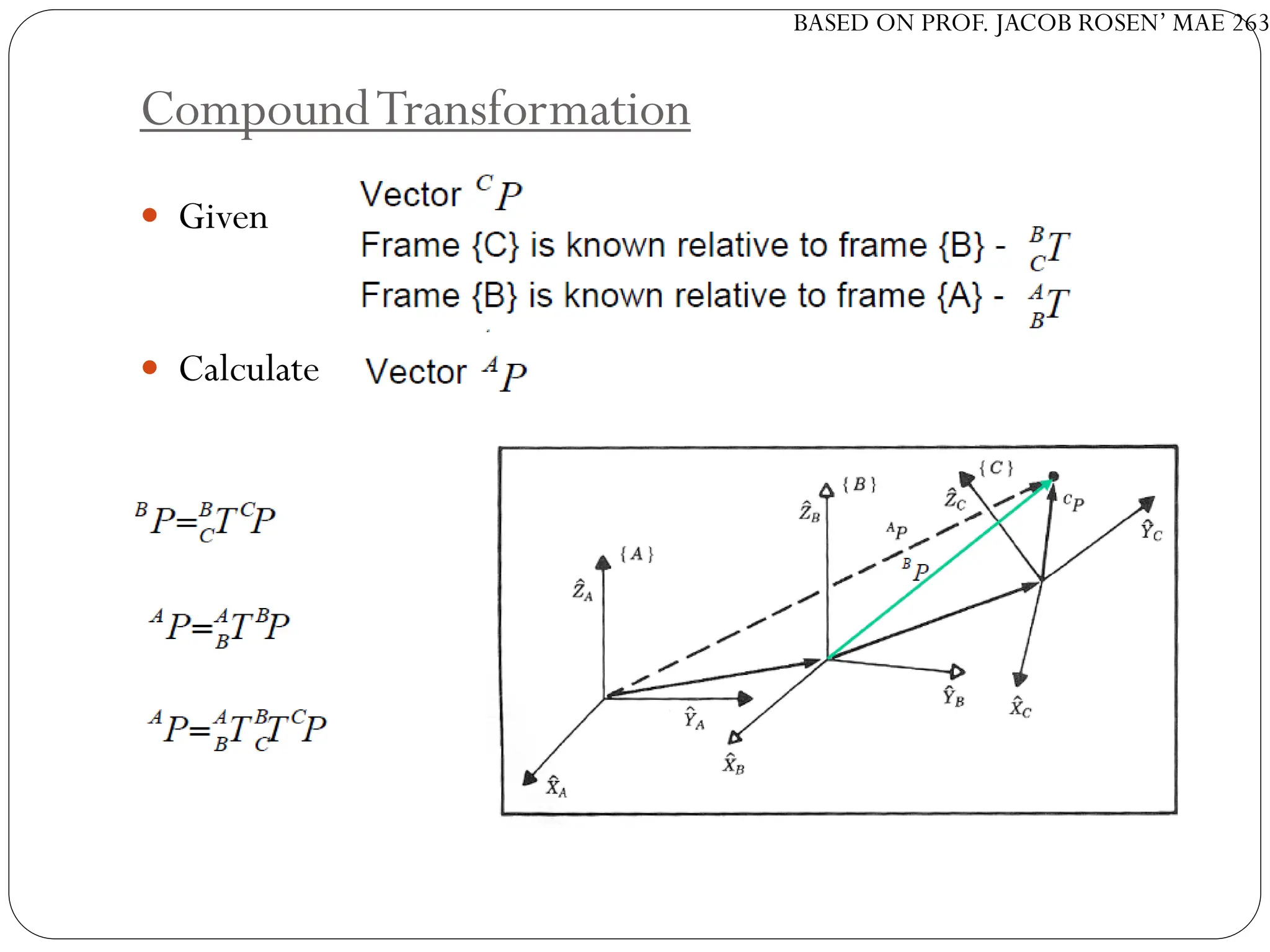
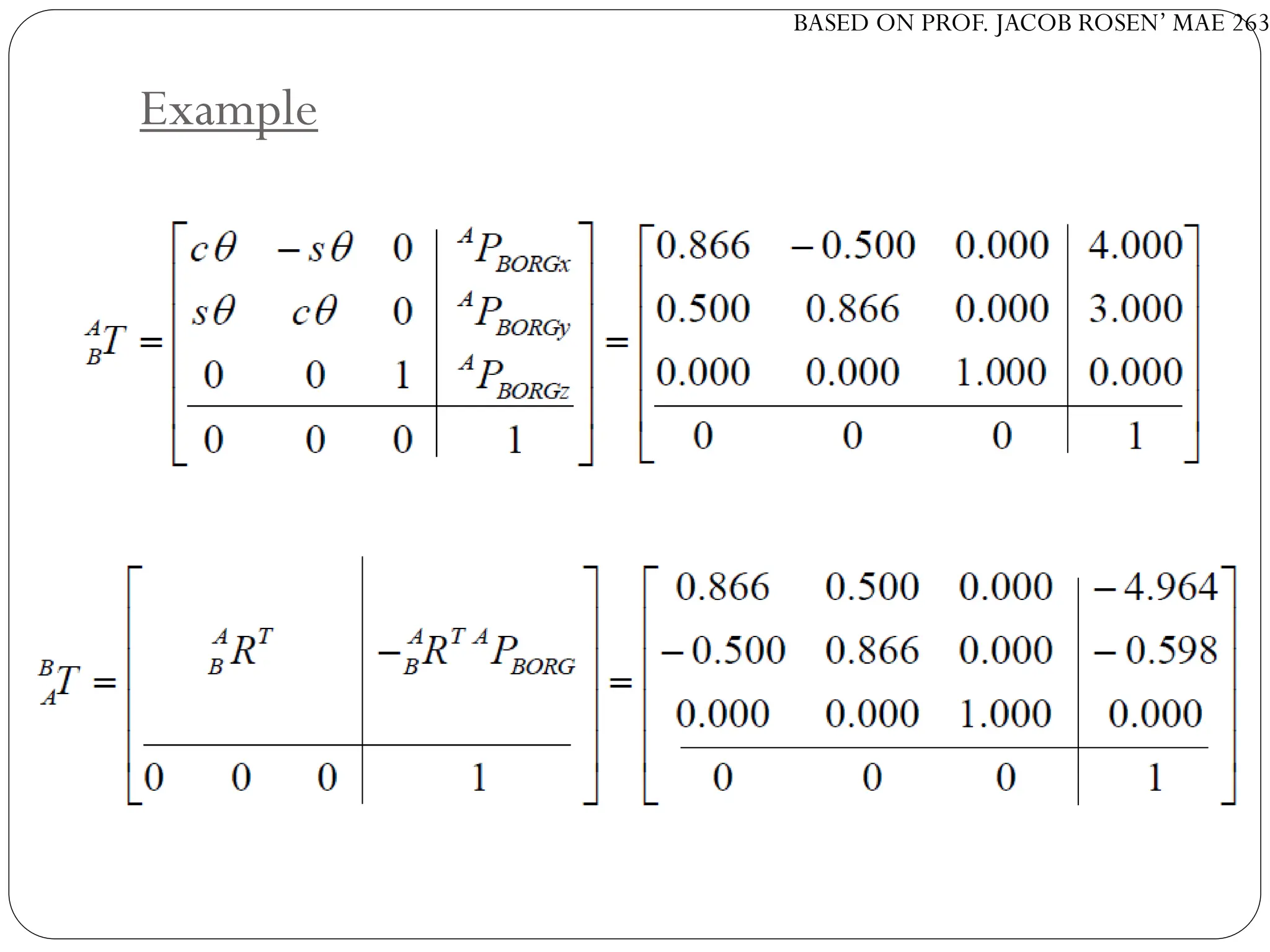
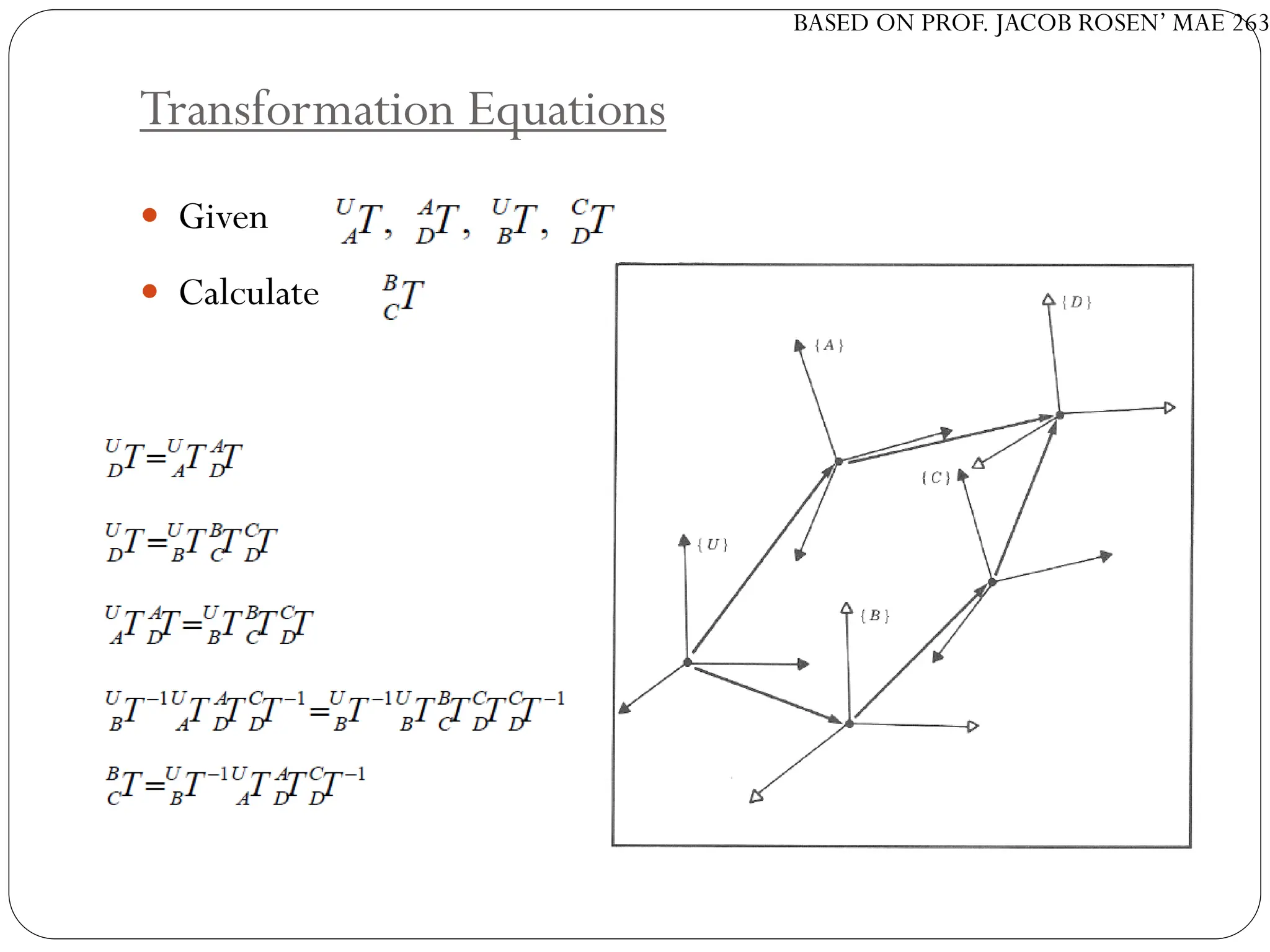
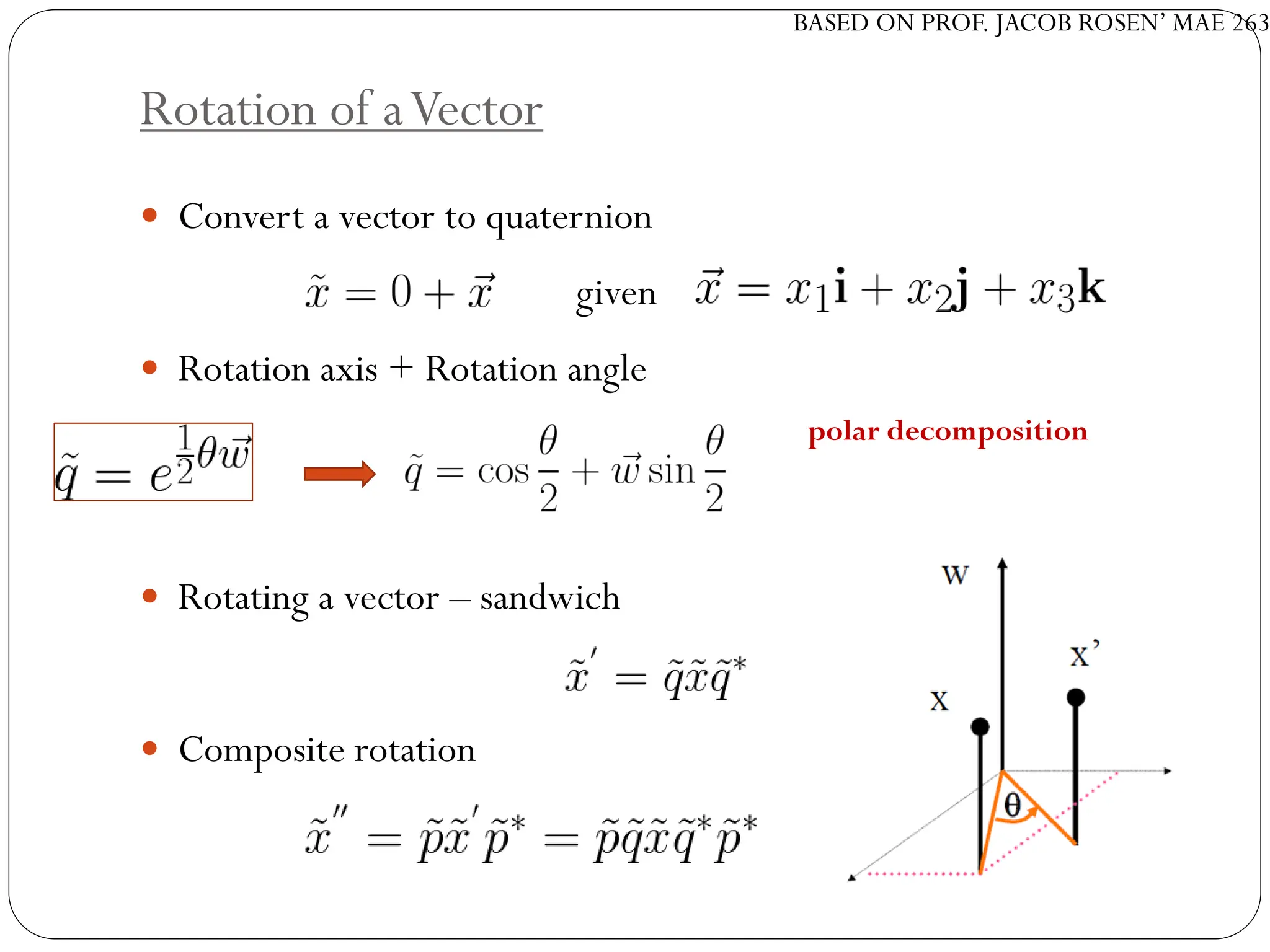
The document discusses motion planning in robotics, focusing on rigid-body transformations and their various representations, including Euler angles, homogeneous transformations, and quaternions. It emphasizes the importance of understanding rotations and translations in both fixed and moving frames, and highlights the limitations such as gimbal lock. Different transformation techniques are compared for their efficiency and applicability in motion planning contexts.

1. RBE 550 MOTION PLANNING
BASED ON DR. DMITRY BERENSON’S RBE
550
Jane Li
Assistant Professor
Mechanical Engineering & Robotics Engineering
http://users.wpi.edu/~zli11
Transformation

2. Announcement
 Project Presentation
 # individual projectVS # team project
 All or some?

3. BASED ON PROF. JACOB ROSEN’ MAE 263
Representation of Rigid-body Configurations
 Parameterization matter!

4. BASED ON PROF. JACOB ROSEN’ MAE 263
Representation of Rigid-body Configurations
 Many representations
 Euler angle
 Homogeneous transformation
 Quaternions
 Different representations have pros and cons

5. BASED ON PROF. JACOB ROSEN’ MAE 263
Transformations
 An understanding of 2D and 3D rigid-body transformations is key
to motion planning
 There is no “best” representation
 Each representation is useful in a different way

6. BASED ON PROF. JACOB ROSEN’ MAE 263
Right-handed Coordinate System

7. BASED ON PROF. JACOB ROSEN’ MAE 263
Representation for a Position
 3X1 position vector in a reference coordinate system

8. BASED ON PROF. JACOB ROSEN’ MAE 263
Representation for a Rotation
 Attach a frame to the Body B
 Rotation of Body B with respect to Frame A

9. BASED ON PROF. JACOB ROSEN’ MAE 263
Representation of a Frame
 Complete specification of a 3D object
 Position + Orientation

10. BASED ON PROF. JACOB ROSEN’ MAE 263
Translation of Frame
 Translation of Frame B with respect to Frame A

11. BASED ON PROF. JACOB ROSEN’ MAE 263
Rotation of a Frame
 Rotation of Frame B with respect to Frame A

12. BASED ON PROF. JACOB ROSEN’ MAE 263
Inverse a Rotation Frame
 Given
 Rotation matrix from Frame B with respect to Frame A 𝑅
𝐵
𝐴
 Calculate
 Rotation matrix from Frame A with respect to Frame B 𝑅
𝐴
𝐵

13. BASED ON PROF. JACOB ROSEN’ MAE 263
Inverse a Rotation Frame

14. BASED ON PROF. JACOB ROSEN’ MAE 263
Rotation Frames - Example
 Given
 Calculate
 Solution

15. BASED ON PROF. JACOB ROSEN’ MAE 263
Rotation Frames - Example

16. BASED ON PROF. JACOB ROSEN’ MAE 263
Rotation Frames - Example

17. BASED ON PROF. JACOB ROSEN’ MAE 263
Rotation about X,Y, and Z-axis
 Rotation matrices
 Rotation about
 A fixed reference frame
 A moving reference frame – Euler Angle

18. BASED ON PROF. JACOB ROSEN’ MAE 263
Rotation about a Fixed Frame
 Each rotation of Frame B takes place about an axis in Frame A

19. BASED ON PROF. JACOB ROSEN’ MAE 263
Rotation about a Fixed Frame
 Compute rotation with respect to (World) Frame A

20. BASED ON PROF. JACOB ROSEN’ MAE 263
Rotation about a Fixed Frame
 Special case

21. BASED ON PROF. JACOB ROSEN’ MAE 263
Rotation about a Moving Frame – Euler Angle
 Each rotation of Frame B takes place about an axis in Frame B

22. BASED ON PROF. JACOB ROSEN’ MAE 263
Rotation about a Moving Frame – Euler Angle
 Compute rotation with respect to (local) Frame B

23. BASED ON PROF. JACOB ROSEN’ MAE 263
Fixed AngleVS Euler Angle
 Same result, but different operation order

24. BASED ON PROF. JACOB ROSEN’ MAE 263
Gimbal Lock
 Because rotations are performed in orders about moving axis
 Previous operation affects the next operation

25. BASED ON PROF. JACOB ROSEN’ MAE 263
Gimbal Lock

26. RBE 550 MOTION PLANNING
BASED ON DR. DMITRY BERENSON’S RBE
550
Gimbal Lock – Singularity Example
 Singularities
 Multiple EulerAngles map to one rotation (Gimbal Lock)
 Let’s say this is our convention:
 Lets set β = 0
 Multiplying through, we get:
 Simplify: α and γ do the same thing!
We have lost a degree
of freedom!

27. HomogeneousTransformation

28. BASED ON PROF. JACOB ROSEN’ MAE 263
General Frame =Translation + Rotation
 Frame B with respect to Frame A

29. BASED ON PROF. JACOB ROSEN’ MAE 263
HomogeneousTransformation
 Translation and Rotation in a single matrix
 Which one is performed first?

30. BASED ON PROF. JACOB ROSEN’ MAE 263
First Rotation,ThenTranslation

31. BASED ON PROF. JACOB ROSEN’ MAE 263
Example
 Given
 Manipulation
 Rotate Frame B about Z-axis of Frame A by 30 deg, then
 Translate 10 units along X-axis and 5 units along Y-axis, in Frame A
 Find
 in FrameA

32. BASED ON PROF. JACOB ROSEN’ MAE 263
Example

33. BASED ON PROF. JACOB ROSEN’ MAE 263
CompoundTransformation
 Given
 Calculate

34. BASED ON PROF. JACOB ROSEN’ MAE 263
InvertedTransformation
 Given
 Calculate

35. BASED ON PROF. JACOB ROSEN’ MAE 263
Example
 Given
 Manipulation
 Rotate Frame B about Z-axis of FrameA by 30 deg, then
 Translate 4 units along X-axis and 3 units alongY-axis, in FrameA
 Find

36. BASED ON PROF. JACOB ROSEN’ MAE 263
Example

37. BASED ON PROF. JACOB ROSEN’ MAE 263
Transformation Equations
 Given
 Calculate

38. BASED ON PROF. JACOB ROSEN’ MAE 263
Quaternion

39. BASED ON PROF. JACOB ROSEN’ MAE 263
Quaternions
 Generalizations of complex numbers
 Identities

40. BASED ON PROF. JACOB ROSEN’ MAE 263
Intuition from Complex Numbers
 Use a second “imaginary” dimension
 Permits manipulation of rotations like a vector
i
θ
Rotation about 3 axes

41. BASED ON PROF. JACOB ROSEN’ MAE 263
Notation
 4-tuples
 Hyper-complex number
 Real + Imaginary
 Ordered doublet
 Exponential

42. BASED ON PROF. JACOB ROSEN’ MAE 263
Operation
 Addition
 Multiplication
Non-commutative

43. BASED ON PROF. JACOB ROSEN’ MAE 263
Operation
 Conjugate – just like a complex number
 Dot product
 Norm
 Product with conjugate = dot product
Another way to compute norm

44. BASED ON PROF. JACOB ROSEN’ MAE 263
Operation
 Inverse
 Therefore
 Note that for unit quaternion,

45. BASED ON PROF. JACOB ROSEN’ MAE 263
Rotation of aVector
 Convert a vector to quaternion
given
 Rotation axis + Rotation angle
 Rotating a vector – sandwich
 Composite rotation
polar decomposition

46. BASED ON PROF. JACOB ROSEN’ MAE 263
Quaternion to Rotation Matrix
 For a quaternion
 Rotation matrix

47. BASED ON PROF. JACOB ROSEN’ MAE 263
Comparison
 Euler angle
 Intuitive
 Rotation and translation are separate
 Gimbal lock -Transformation is not unique at singularity
 HomogenousTransform
 Intuitive
 Rotation +Translation in one shot
 Not compact
 Quaternion
 Rotation and translation are separate, but in the same format
 Fancy math, less intuitive
 Compact format – efficient for the computation of some problems

48. BASED ON PROF. JACOB ROSEN’ MAE 263
Readings