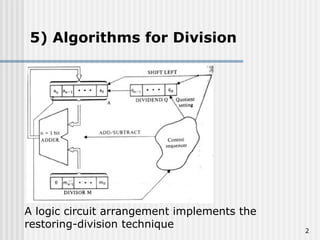
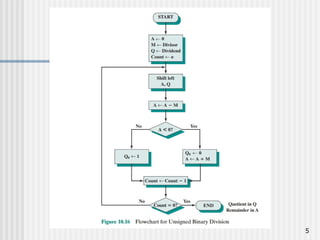
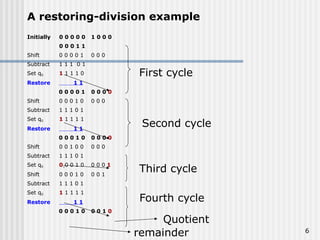
The document describes two algorithms for division: restoring and non-restoring. The restoring-division algorithm involves shifting and subtracting, with a restoration step if subtraction is unsuccessful, while the non-restoring algorithm simplifies this by shifting and either subtracting or adding based on the sign of the result. Both algorithms assume positive values for the divisor and dividend and include examples and references for further reading.

1. 1
Division can be implemented using either a
restoring or a non-restoring algorithm. An
inner loop to perform multiple subtractions
must be incorporated into the algorithm.
Algorithms for Division
10
11 ) 1000
11_
10

2. 2
5) Algorithms for Division
A logic circuit arrangement implements the
restoring-division technique

3. 3
The algorithm assumes that the divisor V and the
dividend D are positive and that |V| < |D|. If |V|
= |D|, then the quotient Q = 1 and the remainder
R = 0. If |V| > |D|, then Q = 0 and R = D.

4. 4
5) Algorithms for Division
The restoring-division algorithm:
S1: DO n times
Shift A and Q left one binary position.
Subtract M from A, placing the answer back in A.
If the sign of A is 1, set q0 to 0 and add M back to
A (restore A); otherwise, set q0 to 1.

5. 5

6. 6
A restoring-division example
Initially 0 0 0 0 0 1 0 0 0
0 0 0 1 1
Shift 0 0 0 0 1 0 0 0
Subtract 1 1 1 0 1
Set q0 1 1 1 1 0
Restore 1 1
0 0 0 0 1 0 0 0 0
Shift 0 0 0 1 0 0 0 0
Subtract 1 1 1 0 1
Set q0 1 1 1 1 1
Restore 1 1
0 0 0 1 0 0 0 0 0
Shift 0 0 1 0 0 0 0 0
Subtract 1 1 1 0 1
Set q0 0 0 0 1 0 0 0 0 1
Shift 0 0 0 1 0 0 0 1
Subtract 1 1 1 0 1
Set q0 1 1 1 1 1
Restore 1 1
0 0 0 1 0 0 0 1 0
remainder
Quotient
First cycle
Second cycle
Third cycle
Fourth cycle

7. 7

8. 8

9. 9
The restoring-division algorithm can be improved by
avoiding the need for restoring A after an unsuccessful
subtraction. Subtraction is said to be unsuccessful if the
result is negative.

10. 10
5) Algorithms for Division
The non-restoring division algorithm:
S1: Do n times
If the sign of A is 0, shift A and Q left one
binary position and subtract M from A;
otherwise, shift A and Q left and add M to A.
S2: If the sign of A is 1, add M to A.

11. 11

12. 12
References:
Computer Systems Organization & Architecture, Addison Wesley
Longman, Inc., 2001
Introduction to Computer Organization 4th
Edition. V.Carl
hamacher. 1998
http:// www.sfxavier.ac.uk/computing/bcd/bcd1.htm
http:// www.awl.com/carpinelli